HATSolver: Learning Groebner Bases with Hierarchical Attention Transformers

At NeurIPS 2024, Kera et al. introduced the use of transformers for computing Groebner bases, a central object in computer algebra with numerous practical applications. In this paper, we improve this approach by applying Hierarchical Attention Transformers (HATs) to solve systems of multivariate polynomial equations via Groebner bases computation. The HAT architecture incorporates a tree-structured inductive bias that enables the modeling of hierarchical relationships present in the data and thus achieves significant computational savings compared to conventional flat attention models. We generalize to arbitrary depths and include a detailed computational cost analysis. Combined with curriculum learning, our method solves instances that are much larger than those in Kera et al. (2024 Learning to compute Groebner bases)

SALSA PICANTE: a machine learning attack on LWE with binary secrets

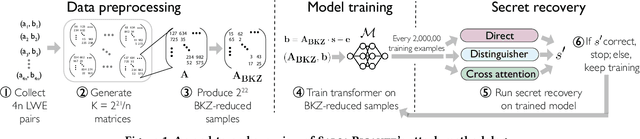
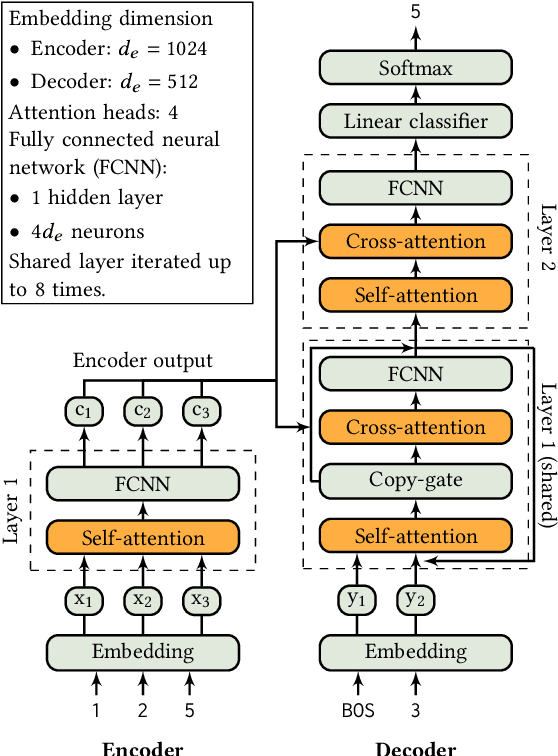
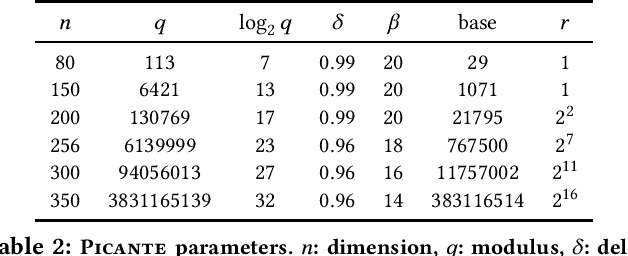
The Learning With Errors (LWE) problem is one of the major hard problems in post-quantum cryptography. For example, 1) the only Key Exchange Mechanism KEM standardized by NIST [14] is based on LWE; and 2) current publicly available Homomorphic Encryption (HE) libraries are based on LWE. NIST KEM schemes use random secrets, but homomorphic encryption schemes use binary or ternary secrets, for efficiency reasons. In particular, sparse binary secrets have been proposed, but not standardized [2], for HE. Prior work SALSA [49] demonstrated a new machine learning attack on sparse binary secrets for the LWE problem in small dimensions (up to n = 128) and low Hamming weights (up to h = 4). However, this attack assumed access to millions of LWE samples, and was not scaled to higher Hamming weights or dimensions. Our attack, PICANTE, reduces the number of samples required to just m = 4n samples. Moreover, it can recover secrets with much larger dimensions (up to 350) and Hamming weights (roughly n/10, or h = 33 for n = 300). To achieve this, we introduce a preprocessing step which allows us to generate the training data from a linear number of samples and changes the distribution of the training data to improve transformer training. We also improve the distinguisher/secret recovery methods of SALSA and introduce a novel cross-attention recovery mechanism which allows us to read-off the secret directly from the trained models.