Isaac Lab: A GPU-Accelerated Simulation Framework for Multi-Modal Robot Learning

We present Isaac Lab, the natural successor to Isaac Gym, which extends the paradigm of GPU-native robotics simulation into the era of large-scale multi-modal learning. Isaac Lab combines high-fidelity GPU parallel physics, photorealistic rendering, and a modular, composable architecture for designing environments and training robot policies. Beyond physics and rendering, the framework integrates actuator models, multi-frequency sensor simulation, data collection pipelines, and domain randomization tools, unifying best practices for reinforcement and imitation learning at scale within a single extensible platform. We highlight its application to a diverse set of challenges, including whole-body control, cross-embodiment mobility, contact-rich and dexterous manipulation, and the integration of human demonstrations for skill acquisition. Finally, we discuss upcoming integration with the differentiable, GPU-accelerated Newton physics engine, which promises new opportunities for scalable, data-efficient, and gradient-based approaches to robot learning. We believe Isaac Lab's combination of advanced simulation capabilities, rich sensing, and data-center scale execution will help unlock the next generation of breakthroughs in robotics research.

Salsa Fresca: Angular Embeddings and Pre-Training for ML Attacks on Learning With Errors

Learning with Errors (LWE) is a hard math problem underlying recently standardized post-quantum cryptography (PQC) systems for key exchange and digital signatures. Prior work proposed new machine learning (ML)-based attacks on LWE problems with small, sparse secrets, but these attacks require millions of LWE samples to train on and take days to recover secrets. We propose three key methods -- better preprocessing, angular embeddings and model pre-training -- to improve these attacks, speeding up preprocessing by $25\times$ and improving model sample efficiency by $10\times$. We demonstrate for the first time that pre-training improves and reduces the cost of ML attacks on LWE. Our architecture improvements enable scaling to larger-dimension LWE problems: this work is the first instance of ML attacks recovering sparse binary secrets in dimension $n=1024$, the smallest dimension used in practice for homomorphic encryption applications of LWE where sparse binary secrets are proposed.

SALSA PICANTE: a machine learning attack on LWE with binary secrets

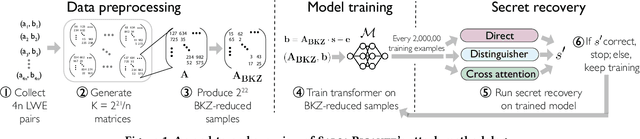
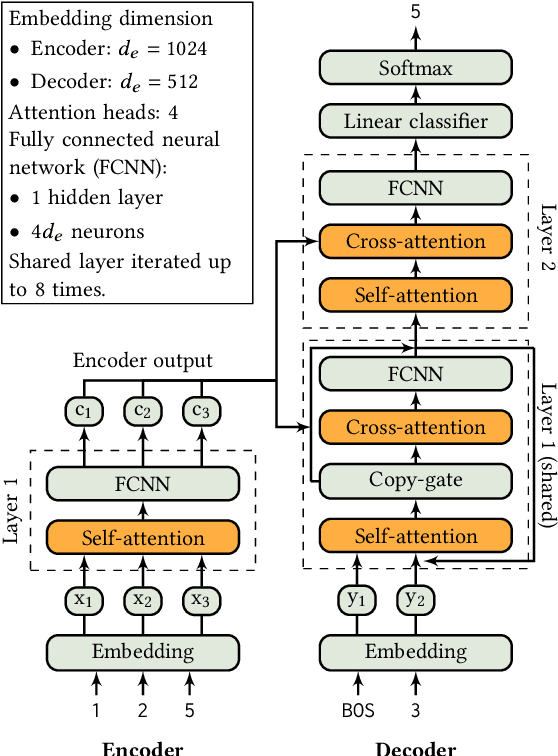
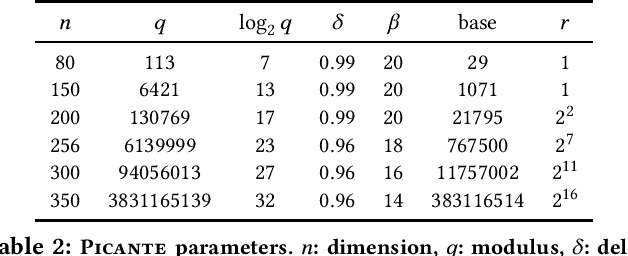
The Learning With Errors (LWE) problem is one of the major hard problems in post-quantum cryptography. For example, 1) the only Key Exchange Mechanism KEM standardized by NIST [14] is based on LWE; and 2) current publicly available Homomorphic Encryption (HE) libraries are based on LWE. NIST KEM schemes use random secrets, but homomorphic encryption schemes use binary or ternary secrets, for efficiency reasons. In particular, sparse binary secrets have been proposed, but not standardized [2], for HE. Prior work SALSA [49] demonstrated a new machine learning attack on sparse binary secrets for the LWE problem in small dimensions (up to n = 128) and low Hamming weights (up to h = 4). However, this attack assumed access to millions of LWE samples, and was not scaled to higher Hamming weights or dimensions. Our attack, PICANTE, reduces the number of samples required to just m = 4n samples. Moreover, it can recover secrets with much larger dimensions (up to 350) and Hamming weights (roughly n/10, or h = 33 for n = 300). To achieve this, we introduce a preprocessing step which allows us to generate the training data from a linear number of samples and changes the distribution of the training data to improve transformer training. We also improve the distinguisher/secret recovery methods of SALSA and introduce a novel cross-attention recovery mechanism which allows us to read-off the secret directly from the trained models.