Randomization for adversarial robustness: the Good, the Bad and the Ugly

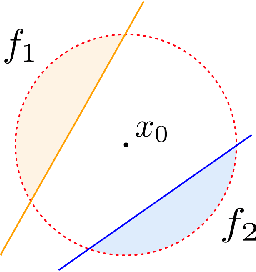
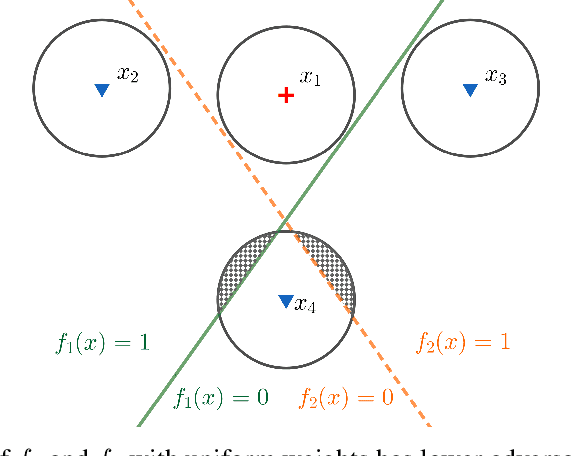
Deep neural networks are known to be vulnerable to adversarial attacks: A small perturbation that is imperceptible to a human can easily make a well-trained deep neural network misclassify. To defend against adversarial attacks, randomized classifiers have been proposed as a robust alternative to deterministic ones. In this work we show that in the binary classification setting, for any randomized classifier, there is always a deterministic classifier with better adversarial risk. In other words, randomization is not necessary for robustness. In many common randomization schemes, the deterministic classifiers with better risk are explicitly described: For example, we show that ensembles of classifiers are more robust than mixtures of classifiers, and randomized smoothing is more robust than input noise injection. Finally, experiments confirm our theoretical results with the two families of randomized classifiers we analyze.

Towards Consistency in Adversarial Classification

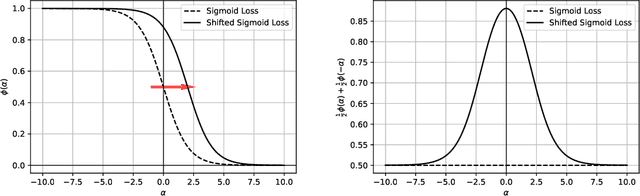
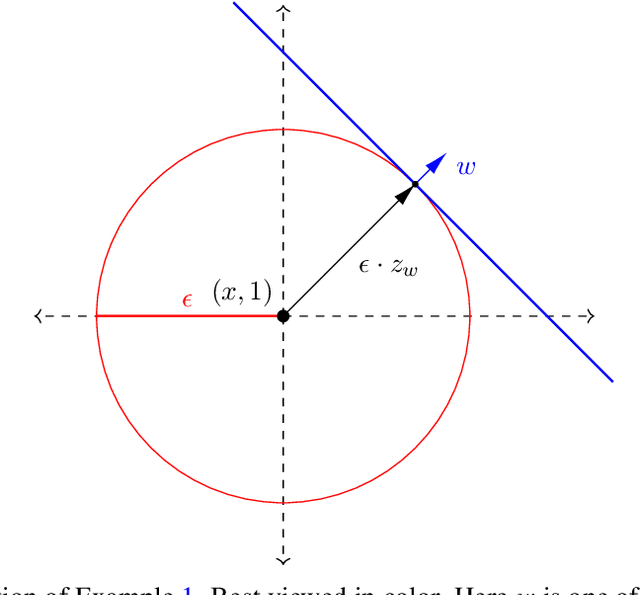
In this paper, we study the problem of consistency in the context of adversarial examples. Specifically, we tackle the following question: can surrogate losses still be used as a proxy for minimizing the $0/1$ loss in the presence of an adversary that alters the inputs at test-time? Different from the standard classification task, this question cannot be reduced to a point-wise minimization problem, and calibration needs not to be sufficient to ensure consistency. In this paper, we expose some pathological behaviors specific to the adversarial problem, and show that no convex surrogate loss can be consistent or calibrated in this context. It is therefore necessary to design another class of surrogate functions that can be used to solve the adversarial consistency issue. As a first step towards designing such a class, we identify sufficient and necessary conditions for a surrogate loss to be calibrated in both the adversarial and standard settings. Finally, we give some directions for building a class of losses that could be consistent in the adversarial framework.

An $\ell^p$-based Kernel Conditional Independence Test

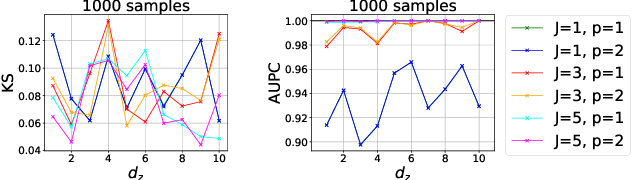
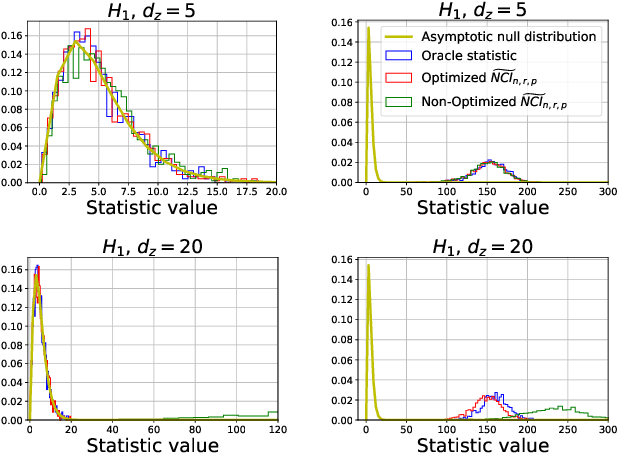
We propose a new computationally efficient test for conditional independence based on the $L^{p}$ distance between two kernel-based representatives of well suited distributions. By evaluating the difference of these two representatives at a finite set of locations, we derive a finite dimensional approximation of the $L^{p}$ metric, obtain its asymptotic distribution under the null hypothesis of conditional independence and design a simple statistical test from it. The test obtained is consistent and computationally efficient. We conduct a series of experiments showing that the performance of our new tests outperforms state-of-the-art methods both in term of statistical power and type-I error even in the high dimensional setting.

Scalable Lipschitz Residual Networks with Convex Potential Flows

The Lipschitz constant of neural networks has been established as a key property to enforce the robustness of neural networks to adversarial examples. However, recent attempts to build $1$-Lipschitz Neural Networks have all shown limitations and robustness have to be traded for accuracy and scalability or vice versa. In this work, we first show that using convex potentials in a residual network gradient flow provides a built-in $1$-Lipschitz transformation. From this insight, we leverage the work on Input Convex Neural Networks to parametrize efficient layers with this property. A comprehensive set of experiments on CIFAR-10 demonstrates the scalability of our architecture and the benefit of our approach for $\ell_2$ provable defenses. Indeed, we train very deep and wide neural networks (up to $1000$ layers) and reach state-of-the-art results in terms of standard and certified accuracy, along with empirical robustness, in comparison with other $1$-Lipschitz architectures.

Asymptotic convergence rates for averaging strategies

Parallel black box optimization consists in estimating the optimum of a function using $\lambda$ parallel evaluations of $f$. Averaging the $\mu$ best individuals among the $\lambda$ evaluations is known to provide better estimates of the optimum of a function than just picking up the best. In continuous domains, this averaging is typically just based on (possibly weighted) arithmetic means. Previous theoretical results were based on quadratic objective functions. In this paper, we extend the results to a wide class of functions, containing three times continuously differentiable functions with unique optimum. We prove formal rate of convergences and show they are indeed better than pure random search asymptotically in $\lambda$. We validate our theoretical findings with experiments on some standard black box functions.

On the robustness of randomized classifiers to adversarial examples

This paper investigates the theory of robustness against adversarial attacks. We focus on randomized classifiers (\emph{i.e.} classifiers that output random variables) and provide a thorough analysis of their behavior through the lens of statistical learning theory and information theory. To this aim, we introduce a new notion of robustness for randomized classifiers, enforcing local Lipschitzness using probability metrics. Equipped with this definition, we make two new contributions. The first one consists in devising a new upper bound on the adversarial generalization gap of randomized classifiers. More precisely, we devise bounds on the generalization gap and the adversarial gap (\emph{i.e.} the gap between the risk and the worst-case risk under attack) of randomized classifiers. The second contribution presents a yet simple but efficient noise injection method to design robust randomized classifiers. We show that our results are applicable to a wide range of machine learning models under mild hypotheses. We further corroborate our findings with experimental results using deep neural networks on standard image datasets, namely CIFAR-10 and CIFAR-100. All robust models we trained models can simultaneously achieve state-of-the-art accuracy (over $0.82$ clean accuracy on CIFAR-10) and enjoy \emph{guaranteed} robust accuracy bounds ($0.45$ against $\ell_2$ adversaries with magnitude $0.5$ on CIFAR-10).

Mixed Nash Equilibria in the Adversarial Examples Game

This paper tackles the problem of adversarial examples from a game theoretic point of view. We study the open question of the existence of mixed Nash equilibria in the zero-sum game formed by the attacker and the classifier. While previous works usually allow only one player to use randomized strategies, we show the necessity of considering randomization for both the classifier and the attacker. We demonstrate that this game has no duality gap, meaning that it always admits approximate Nash equilibria. We also provide the first optimization algorithms to learn a mixture of classifiers that approximately realizes the value of this game, \emph{i.e.} procedures to build an optimally robust randomized classifier.

Adversarial Robustness by Design through Analog Computing and Synthetic Gradients

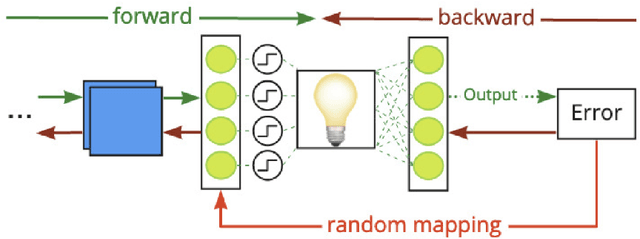
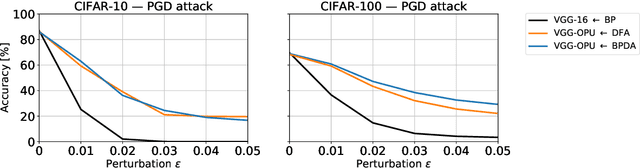
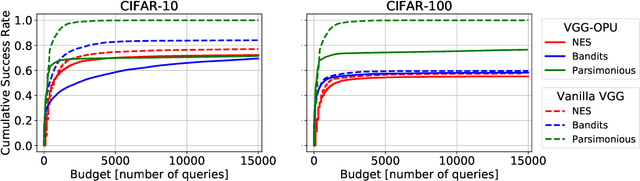
We propose a new defense mechanism against adversarial attacks inspired by an optical co-processor, providing robustness without compromising natural accuracy in both white-box and black-box settings. This hardware co-processor performs a nonlinear fixed random transformation, where the parameters are unknown and impossible to retrieve with sufficient precision for large enough dimensions. In the white-box setting, our defense works by obfuscating the parameters of the random projection. Unlike other defenses relying on obfuscated gradients, we find we are unable to build a reliable backward differentiable approximation for obfuscated parameters. Moreover, while our model reaches a good natural accuracy with a hybrid backpropagation - synthetic gradient method, the same approach is suboptimal if employed to generate adversarial examples. We find the combination of a random projection and binarization in the optical system also improves robustness against various types of black-box attacks. Finally, our hybrid training method builds robust features against transfer attacks. We demonstrate our approach on a VGG-like architecture, placing the defense on top of the convolutional features, on CIFAR-10 and CIFAR-100. Code is available at https://github.com/lightonai/adversarial-robustness-by-design.

Advocating for Multiple Defense Strategies against Adversarial Examples

It has been empirically observed that defense mechanisms designed to protect neural networks against $\ell_\infty$ adversarial examples offer poor performance against $\ell_2$ adversarial examples and vice versa. In this paper we conduct a geometrical analysis that validates this observation. Then, we provide a number of empirical insights to illustrate the effect of this phenomenon in practice. Then, we review some of the existing defense mechanism that attempts to defend against multiple attacks by mixing defense strategies. Thanks to our numerical experiments, we discuss the relevance of this method and state open questions for the adversarial examples community.

Black-Box Optimization Revisited: Improving Algorithm Selection Wizards through Massive Benchmarking

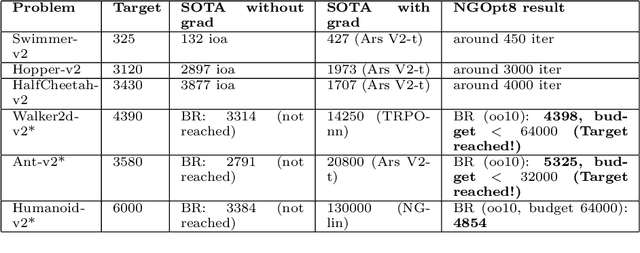
Existing studies in black-box optimization suffer from low generalizability, caused by a typically selective choice of problem instances used for training and testing different optimization algorithms. Among other issues, this practice promotes overfitting and poor-performing user guide-lines. To address this shortcoming, we propose in this work a benchmark suite which covers a broad range of black-box optimization problems, ranging from academic benchmarks to real-world optimization problems, from discrete over numerical to mixed-integer problems, from small to very large-scale problems, from noisy over dynamic to static problems, etc. We demonstrate the advantages of such a broad collection by deriving from it NGOpt8, a general-purpose algorithm selection wizard. Using three different types of algorithm selection techniques, NGOpt8 achieves competitive performance on all benchmark suites. It significantly outperforms previous state of the art on some of them, including the MuJoCo collection,YABBOB, and LSGO. A single algorithm therefore performed best on these three important benchmarks, without any task-specific parametrization. The benchmark collection, the wizard, its low-level solvers, as well as all experimental data are fully reproducible and open source. They are made available as a fork of Nevergrad, termed OptimSuite.