An $\ell^p$-based Kernel Conditional Independence Test
Paper and Code
Oct 28, 2021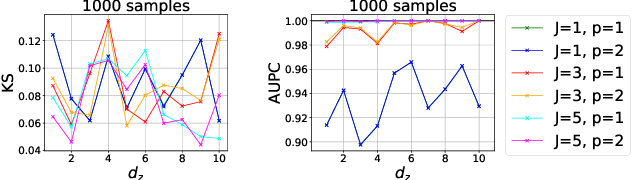
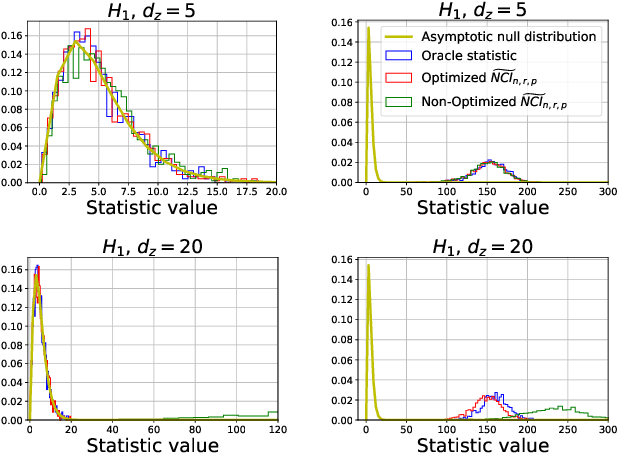


We propose a new computationally efficient test for conditional independence based on the $L^{p}$ distance between two kernel-based representatives of well suited distributions. By evaluating the difference of these two representatives at a finite set of locations, we derive a finite dimensional approximation of the $L^{p}$ metric, obtain its asymptotic distribution under the null hypothesis of conditional independence and design a simple statistical test from it. The test obtained is consistent and computationally efficient. We conduct a series of experiments showing that the performance of our new tests outperforms state-of-the-art methods both in term of statistical power and type-I error even in the high dimensional setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge