Black-Box Optimization Revisited: Improving Algorithm Selection Wizards through Massive Benchmarking

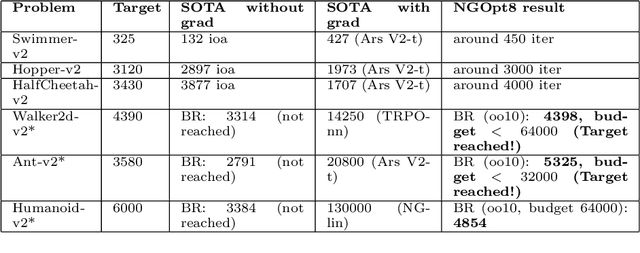
Existing studies in black-box optimization suffer from low generalizability, caused by a typically selective choice of problem instances used for training and testing different optimization algorithms. Among other issues, this practice promotes overfitting and poor-performing user guide-lines. To address this shortcoming, we propose in this work a benchmark suite which covers a broad range of black-box optimization problems, ranging from academic benchmarks to real-world optimization problems, from discrete over numerical to mixed-integer problems, from small to very large-scale problems, from noisy over dynamic to static problems, etc. We demonstrate the advantages of such a broad collection by deriving from it NGOpt8, a general-purpose algorithm selection wizard. Using three different types of algorithm selection techniques, NGOpt8 achieves competitive performance on all benchmark suites. It significantly outperforms previous state of the art on some of them, including the MuJoCo collection,YABBOB, and LSGO. A single algorithm therefore performed best on these three important benchmarks, without any task-specific parametrization. The benchmark collection, the wizard, its low-level solvers, as well as all experimental data are fully reproducible and open source. They are made available as a fork of Nevergrad, termed OptimSuite.

Versatile Black-Box Optimization

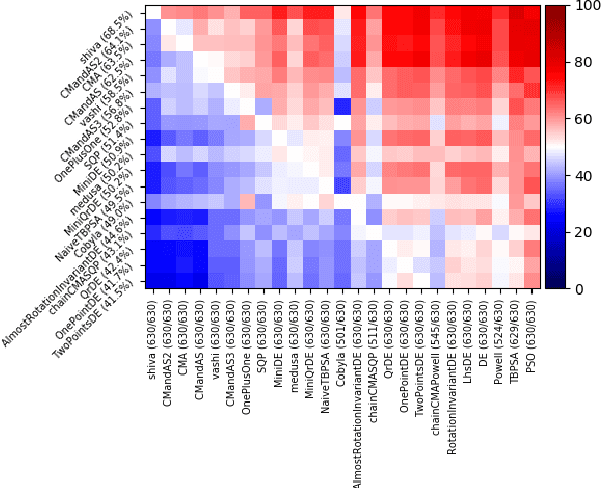
Choosing automatically the right algorithm using problem descriptors is a classical component of combinatorial optimization. It is also a good tool for making evolutionary algorithms fast, robust and versatile. We present Shiwa, an algorithm good at both discrete and continuous, noisy and noise-free, sequential and parallel, black-box optimization. Our algorithm is experimentally compared to competitors on YABBOB, a BBOB comparable testbed, and on some variants of it, and then validated on several real world testbeds.

Optimal estimation for Large-Eddy Simulation of turbulence and application to the analysis of subgrid models

The tools of optimal estimation are applied to the study of subgrid models for Large-Eddy Simulation of turbulence. The concept of optimal estimator is introduced and its properties are analyzed in the context of applications to a priori tests of subgrid models. Attention is focused on the Cook and Riley model in the case of a scalar field in isotropic turbulence. Using DNS data, the relevance of the beta assumption is estimated by computing (i) generalized optimal estimators and (ii) the error brought by this assumption alone. Optimal estimators are computed for the subgrid variance using various sets of variables and various techniques (histograms and neural networks). It is shown that optimal estimators allow a thorough exploration of models. Neural networks are proved to be relevant and very efficient in this framework, and further usages are suggested.