Warmstarting for Scaling Language Models

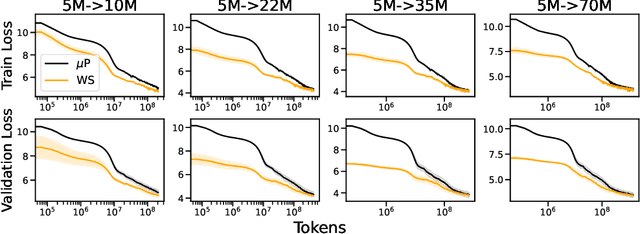
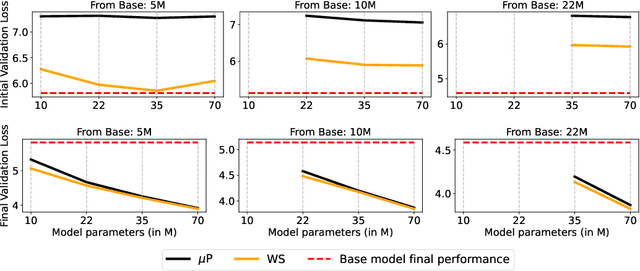
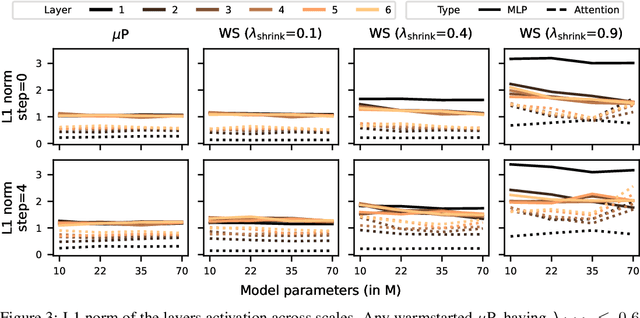
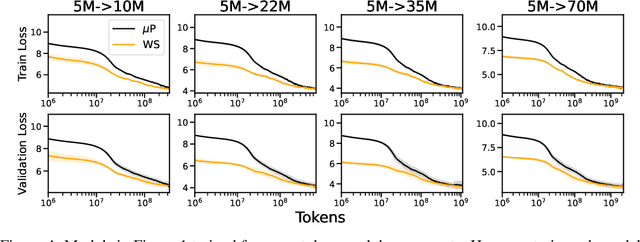
Scaling model sizes to scale performance has worked remarkably well for the current large language models paradigm. The research and empirical findings of various scaling studies led to novel scaling results and laws that guides subsequent research. High training costs for contemporary scales of data and models result in a lack of thorough understanding of how to tune and arrive at such training setups. One direction to ameliorate the cost of pretraining large models is to warmstart the large-scale training from smaller models that are cheaper to tune. In this work, we attempt to understand if the behavior of optimal hyperparameters can be retained under warmstarting for scaling. We explore simple operations that allow the application of theoretically motivated methods of zero-shot transfer of optimal hyperparameters using {\mu}Transfer. We investigate the aspects that contribute to the speedup in convergence and the preservation of stable training dynamics under warmstarting with {\mu}Transfer. We find that shrinking smaller model weights, zero-padding, and perturbing the resulting larger model with scaled initialization from {\mu}P enables effective warmstarting of $\mut{}$.

In-Context Freeze-Thaw Bayesian Optimization for Hyperparameter Optimization

With the increasing computational costs associated with deep learning, automated hyperparameter optimization methods, strongly relying on black-box Bayesian optimization (BO), face limitations. Freeze-thaw BO offers a promising grey-box alternative, strategically allocating scarce resources incrementally to different configurations. However, the frequent surrogate model updates inherent to this approach pose challenges for existing methods, requiring retraining or fine-tuning their neural network surrogates online, introducing overhead, instability, and hyper-hyperparameters. In this work, we propose FT-PFN, a novel surrogate for Freeze-thaw style BO. FT-PFN is a prior-data fitted network (PFN) that leverages the transformers' in-context learning ability to efficiently and reliably do Bayesian learning curve extrapolation in a single forward pass. Our empirical analysis across three benchmark suites shows that the predictions made by FT-PFN are more accurate and 10-100 times faster than those of the deep Gaussian process and deep ensemble surrogates used in previous work. Furthermore, we show that, when combined with our novel acquisition mechanism (MFPI-random), the resulting in-context freeze-thaw BO method (ifBO), yields new state-of-the-art performance in the same three families of deep learning HPO benchmarks considered in prior work.

Efficient Bayesian Learning Curve Extrapolation using Prior-Data Fitted Networks

Learning curve extrapolation aims to predict model performance in later epochs of training, based on the performance in earlier epochs. In this work, we argue that, while the inherent uncertainty in the extrapolation of learning curves warrants a Bayesian approach, existing methods are (i) overly restrictive, and/or (ii) computationally expensive. We describe the first application of prior-data fitted neural networks (PFNs) in this context. A PFN is a transformer, pre-trained on data generated from a prior, to perform approximate Bayesian inference in a single forward pass. We propose LC-PFN, a PFN trained to extrapolate 10 million artificial right-censored learning curves generated from a parametric prior proposed in prior art using MCMC. We demonstrate that LC-PFN can approximate the posterior predictive distribution more accurately than MCMC, while being over 10 000 times faster. We also show that the same LC-PFN achieves competitive performance extrapolating a total of 20 000 real learning curves from four learning curve benchmarks (LCBench, NAS-Bench-201, Taskset, and PD1) that stem from training a wide range of model architectures (MLPs, CNNs, RNNs, and Transformers) on 53 different datasets with varying input modalities (tabular, image, text, and protein data). Finally, we investigate its potential in the context of model selection and find that a simple LC-PFN based predictive early stopping criterion obtains 2 - 6x speed-ups on 45 of these datasets, at virtually no overhead.

Black-Box Optimization Revisited: Improving Algorithm Selection Wizards through Massive Benchmarking

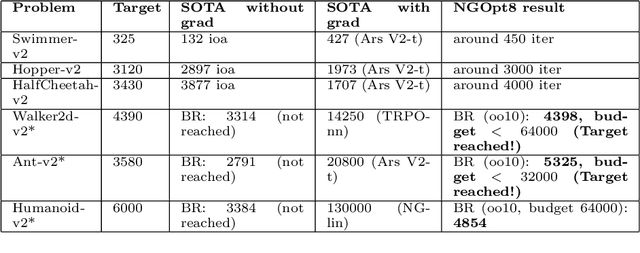
Existing studies in black-box optimization suffer from low generalizability, caused by a typically selective choice of problem instances used for training and testing different optimization algorithms. Among other issues, this practice promotes overfitting and poor-performing user guide-lines. To address this shortcoming, we propose in this work a benchmark suite which covers a broad range of black-box optimization problems, ranging from academic benchmarks to real-world optimization problems, from discrete over numerical to mixed-integer problems, from small to very large-scale problems, from noisy over dynamic to static problems, etc. We demonstrate the advantages of such a broad collection by deriving from it NGOpt8, a general-purpose algorithm selection wizard. Using three different types of algorithm selection techniques, NGOpt8 achieves competitive performance on all benchmark suites. It significantly outperforms previous state of the art on some of them, including the MuJoCo collection,YABBOB, and LSGO. A single algorithm therefore performed best on these three important benchmarks, without any task-specific parametrization. The benchmark collection, the wizard, its low-level solvers, as well as all experimental data are fully reproducible and open source. They are made available as a fork of Nevergrad, termed OptimSuite.

Distribution-Based Invariant Deep Networks for Learning Meta-Features

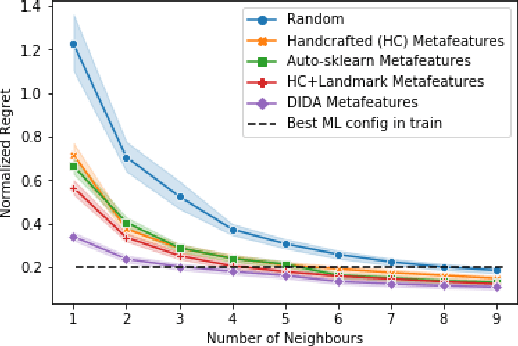
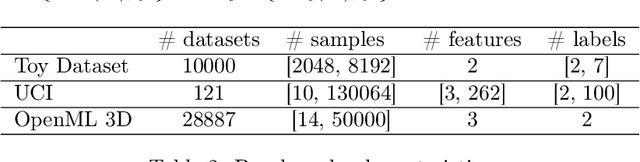
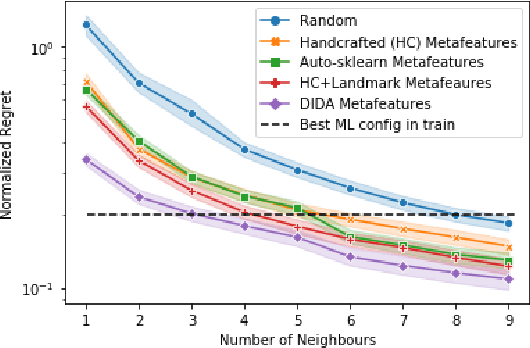
Recent advances in deep learning from probability distributions enable to achieve classification or regression from distribution samples, invariant under permutation of the samples. This paper extends the distribution-based deep neural architectures to achieve classification or regression from distribution samples, invariant under permutation of the descriptive features, too. The motivation for this extension is the Auto-ML problem, aimed to identify a priori the ML configuration best suited to a dataset. Formally, a distribution-based invariant deep learning architecture is presented, and leveraged to extract the meta-features characterizing a dataset. The contribution of the paper is twofold. On the theoretical side, the proposed architecture inherits the NN properties of universal approximation, and the robustness of the approach w.r.t. moderate perturbations is established. On the empirical side, a proof of concept of the approach is proposed, to identify the SVM hyper-parameters best suited to a large benchmark of diversified small size datasets.

Automated Machine Learning with Monte-Carlo Tree Search (Extended Version)

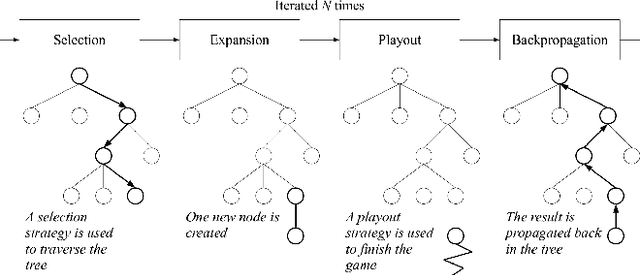
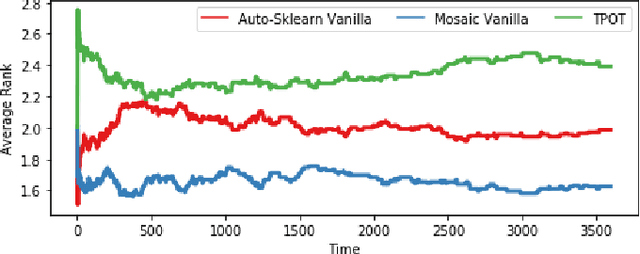
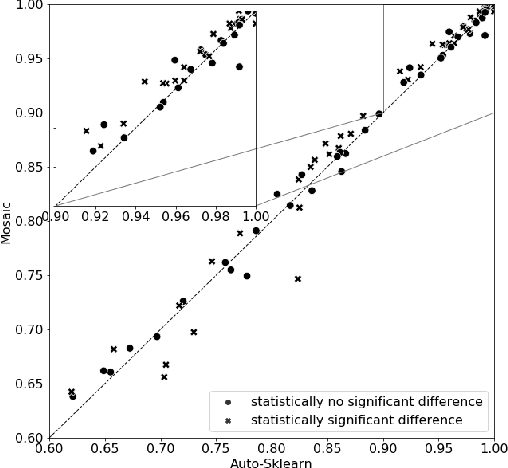
The AutoML task consists of selecting the proper algorithm in a machine learning portfolio, and its hyperparameter values, in order to deliver the best performance on the dataset at hand. Mosaic, a Monte-Carlo tree search (MCTS) based approach, is presented to handle the AutoML hybrid structural and parametric expensive black-box optimization problem. Extensive empirical studies are conducted to independently assess and compare: i) the optimization processes based on Bayesian optimization or MCTS; ii) its warm-start initialization; iii) the ensembling of the solutions gathered along the search. Mosaic is assessed on the OpenML 100 benchmark and the Scikit-learn portfolio, with statistically significant gains over Auto-Sklearn, winner of former international AutoML challenges.