Tune My Adam, Please!

The Adam optimizer remains one of the most widely used optimizers in deep learning, and effectively tuning its hyperparameters is key to optimizing performance. However, tuning can be tedious and costly. Freeze-thaw Bayesian Optimization (BO) is a recent promising approach for low-budget hyperparameter tuning, but is limited by generic surrogates without prior knowledge of how hyperparameters affect learning. We propose Adam-PFN, a new surrogate model for Freeze-thaw BO of Adam's hyperparameters, pre-trained on learning curves from TaskSet, together with a new learning curve augmentation method, CDF-augment, which artificially increases the number of available training examples. Our approach improves both learning curve extrapolation and accelerates hyperparameter optimization on TaskSet evaluation tasks, with strong performance on out-of-distribution (OOD) tasks.

FairPFN: A Tabular Foundation Model for Causal Fairness

Machine learning (ML) systems are utilized in critical sectors, such as healthcare, law enforcement, and finance. However, these systems are often trained on historical data that contains demographic biases, leading to ML decisions that perpetuate or exacerbate existing social inequalities. Causal fairness provides a transparent, human-in-the-loop framework to mitigate algorithmic discrimination, aligning closely with legal doctrines of direct and indirect discrimination. However, current causal fairness frameworks hold a key limitation in that they assume prior knowledge of the correct causal model, restricting their applicability in complex fairness scenarios where causal models are unknown or difficult to identify. To bridge this gap, we propose FairPFN, a tabular foundation model pre-trained on synthetic causal fairness data to identify and mitigate the causal effects of protected attributes in its predictions. FairPFN's key contribution is that it requires no knowledge of the causal model and still demonstrates strong performance in identifying and removing protected causal effects across a diverse set of hand-crafted and real-world scenarios relative to robust baseline methods. FairPFN paves the way for promising future research, making causal fairness more accessible to a wider variety of complex fairness problems.

Position: The Future of Bayesian Prediction Is Prior-Fitted

Training neural networks on randomly generated artificial datasets yields Bayesian models that capture the prior defined by the dataset-generating distribution. Prior-data Fitted Networks (PFNs) are a class of methods designed to leverage this insight. In an era of rapidly increasing computational resources for pre-training and a near stagnation in the generation of new real-world data in many applications, PFNs are poised to play a more important role across a wide range of applications. They enable the efficient allocation of pre-training compute to low-data scenarios. Originally applied to small Bayesian modeling tasks, the field of PFNs has significantly expanded to address more complex domains and larger datasets. This position paper argues that PFNs and other amortized inference approaches represent the future of Bayesian inference, leveraging amortized learning to tackle data-scarce problems. We thus believe they are a fruitful area of research. In this position paper, we explore their potential and directions to address their current limitations.

The Tabular Foundation Model TabPFN Outperforms Specialized Time Series Forecasting Models Based on Simple Features

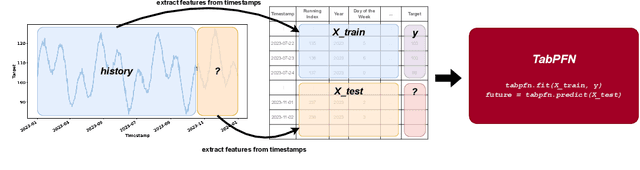
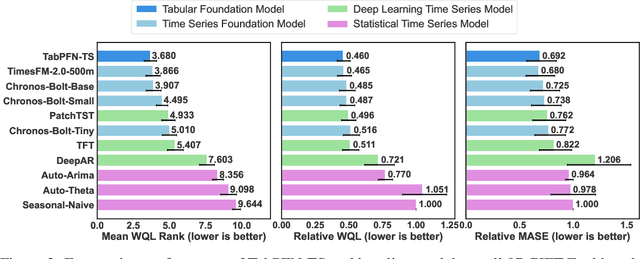
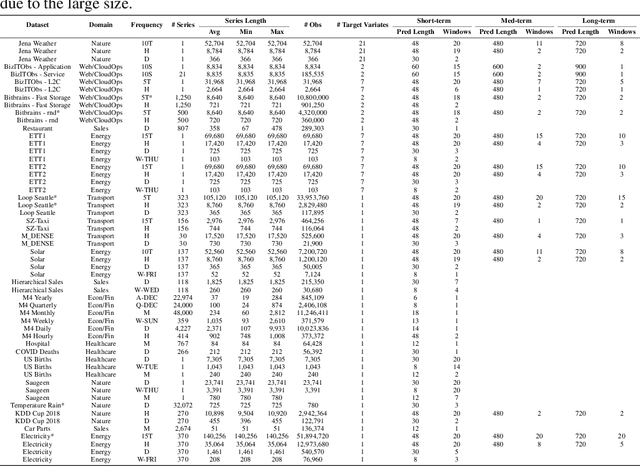
Foundation models have become popular in forecasting due to their ability to make accurate predictions, even with minimal fine-tuning on specific datasets. In this paper, we demonstrate how the newly released regression variant of TabPFN, a general tabular foundation model, can be applied to time series forecasting. We propose a straightforward approach, TabPFN-TS, which pairs TabPFN with simple feature engineering to achieve strong forecasting performance. Despite its simplicity and with only 11M parameters, TabPFN-TS outperforms Chronos-Mini, a model of similar size, and matches or even slightly outperforms Chronos-Large, which has 65-fold more parameters. A key strength of our method lies in its reliance solely on artificial data during pre-training, avoiding the need for large training datasets and eliminating the risk of benchmark contamination.

Drift-Resilient TabPFN: In-Context Learning Temporal Distribution Shifts on Tabular Data

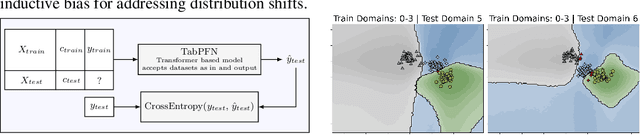
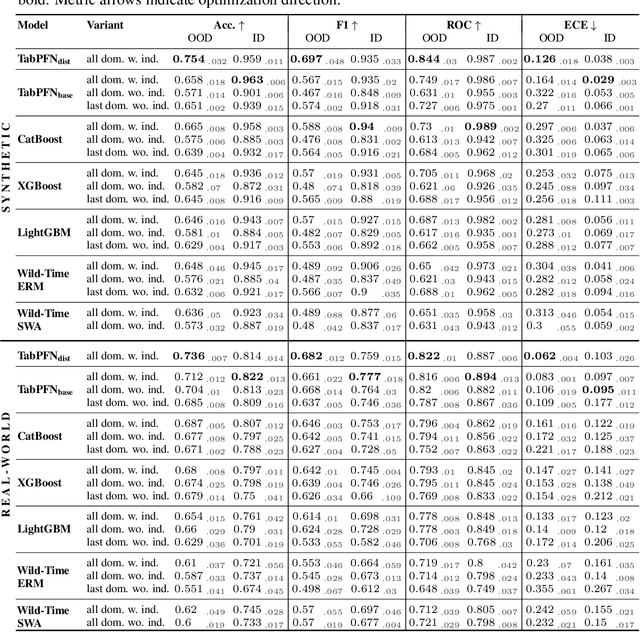
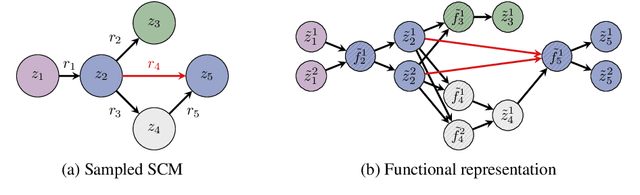
While most ML models expect independent and identically distributed data, this assumption is often violated in real-world scenarios due to distribution shifts, resulting in the degradation of machine learning model performance. Until now, no tabular method has consistently outperformed classical supervised learning, which ignores these shifts. To address temporal distribution shifts, we present Drift-Resilient TabPFN, a fresh approach based on In-Context Learning with a Prior-Data Fitted Network that learns the learning algorithm itself: it accepts the entire training dataset as input and makes predictions on the test set in a single forward pass. Specifically, it learns to approximate Bayesian inference on synthetic datasets drawn from a prior that specifies the model's inductive bias. This prior is based on structural causal models (SCM), which gradually shift over time. To model shifts of these causal models, we use a secondary SCM, that specifies changes in the primary model parameters. The resulting Drift-Resilient TabPFN can be applied to unseen data, runs in seconds on small to moderately sized datasets and needs no hyperparameter tuning. Comprehensive evaluations across 18 synthetic and real-world datasets demonstrate large performance improvements over a wide range of baselines, such as XGB, CatBoost, TabPFN, and applicable methods featured in the Wild-Time benchmark. Compared to the strongest baselines, it improves accuracy from 0.688 to 0.744 and ROC AUC from 0.786 to 0.832 while maintaining stronger calibration. This approach could serve as significant groundwork for further research on out-of-distribution prediction.

Bayes' Power for Explaining In-Context Learning Generalizations

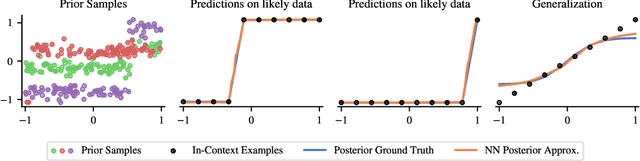
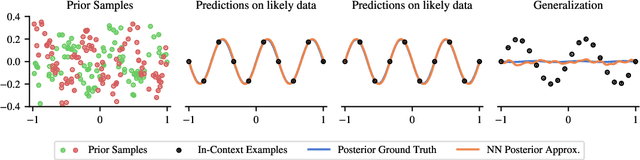
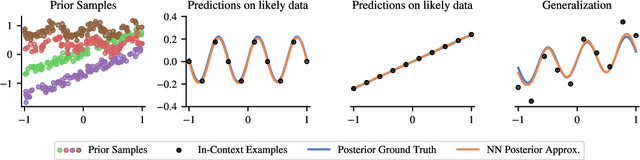
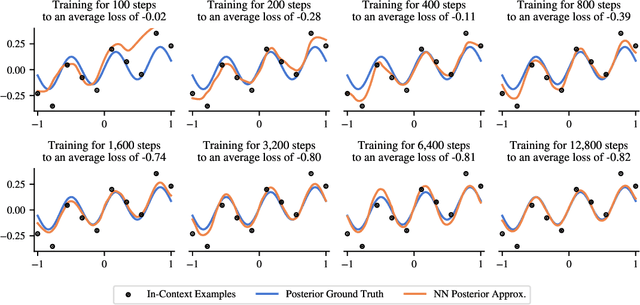
Traditionally, neural network training has been primarily viewed as an approximation of maximum likelihood estimation (MLE). This interpretation originated in a time when training for multiple epochs on small datasets was common and performance was data bound; but it falls short in the era of large-scale single-epoch trainings ushered in by large self-supervised setups, like language models. In this new setup, performance is compute-bound, but data is readily available. As models became more powerful, in-context learning (ICL), i.e., learning in a single forward-pass based on the context, emerged as one of the dominant paradigms. In this paper, we argue that a more useful interpretation of neural network behavior in this era is as an approximation of the true posterior, as defined by the data-generating process. We demonstrate this interpretations' power for ICL and its usefulness to predict generalizations to previously unseen tasks. We show how models become robust in-context learners by effectively composing knowledge from their training data. We illustrate this with experiments that reveal surprising generalizations, all explicable through the exact posterior. Finally, we show the inherent constraints of the generalization capabilities of posteriors and the limitations of neural networks in approximating these posteriors.

Efficient Bayesian Learning Curve Extrapolation using Prior-Data Fitted Networks

Learning curve extrapolation aims to predict model performance in later epochs of training, based on the performance in earlier epochs. In this work, we argue that, while the inherent uncertainty in the extrapolation of learning curves warrants a Bayesian approach, existing methods are (i) overly restrictive, and/or (ii) computationally expensive. We describe the first application of prior-data fitted neural networks (PFNs) in this context. A PFN is a transformer, pre-trained on data generated from a prior, to perform approximate Bayesian inference in a single forward pass. We propose LC-PFN, a PFN trained to extrapolate 10 million artificial right-censored learning curves generated from a parametric prior proposed in prior art using MCMC. We demonstrate that LC-PFN can approximate the posterior predictive distribution more accurately than MCMC, while being over 10 000 times faster. We also show that the same LC-PFN achieves competitive performance extrapolating a total of 20 000 real learning curves from four learning curve benchmarks (LCBench, NAS-Bench-201, Taskset, and PD1) that stem from training a wide range of model architectures (MLPs, CNNs, RNNs, and Transformers) on 53 different datasets with varying input modalities (tabular, image, text, and protein data). Finally, we investigate its potential in the context of model selection and find that a simple LC-PFN based predictive early stopping criterion obtains 2 - 6x speed-ups on 45 of these datasets, at virtually no overhead.

PFNs4BO: In-Context Learning for Bayesian Optimization

In this paper, we use Prior-data Fitted Networks (PFNs) as a flexible surrogate for Bayesian Optimization (BO). PFNs are neural processes that are trained to approximate the posterior predictive distribution (PPD) through in-context learning on any prior distribution that can be efficiently sampled from. We describe how this flexibility can be exploited for surrogate modeling in BO. We use PFNs to mimic a naive Gaussian process (GP), an advanced GP, and a Bayesian Neural Network (BNN). In addition, we show how to incorporate further information into the prior, such as allowing hints about the position of optima (user priors), ignoring irrelevant dimensions, and performing non-myopic BO by learning the acquisition function. The flexibility underlying these extensions opens up vast possibilities for using PFNs for BO. We demonstrate the usefulness of PFNs for BO in a large-scale evaluation on artificial GP samples and three different hyperparameter optimization testbeds: HPO-B, Bayesmark, and PD1. We publish code alongside trained models at https://github.com/automl/PFNs4BO.

GPT for Semi-Automated Data Science: Introducing CAAFE for Context-Aware Automated Feature Engineering

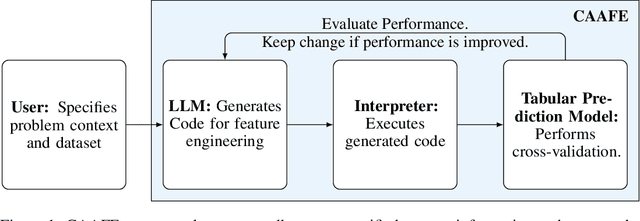
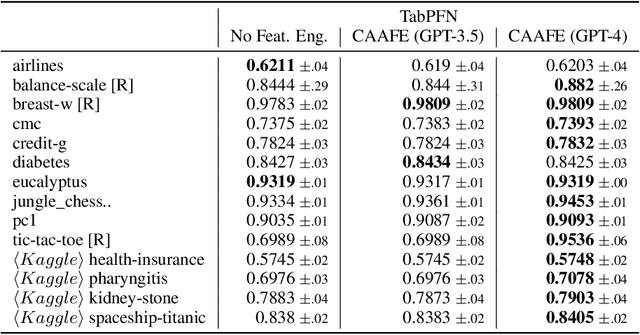
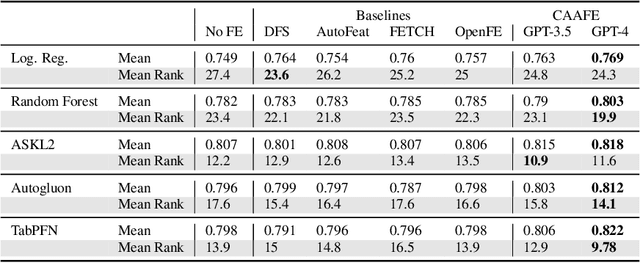
As the field of automated machine learning (AutoML) advances, it becomes increasingly important to include domain knowledge within these systems. We present an approach for doing so by harnessing the power of large language models (LLMs). Specifically, we introduce Context-Aware Automated Feature Engineering (CAAFE), a feature engineering method for tabular datasets that utilizes an LLM to generate additional semantically meaningful features for tabular datasets based on their descriptions. The method produces both Python code for creating new features and explanations for the utility of the generated features. Despite being methodologically simple, CAAFE enhances performance on 11 out of 14 datasets, ties on 2 and looses on 1 - boosting mean ROC AUC performance from 0.798 to 0.822 across all datasets. On the evaluated datasets, this improvement is similar to the average improvement achieved by using a random forest (AUC 0.782) instead of logistic regression (AUC 0.754). Furthermore, our method offers valuable insights into the rationale behind the generated features by providing a textual explanation for each generated feature. CAAFE paves the way for more extensive (semi-)automation in data science tasks and emphasizes the significance of context-aware solutions that can extend the scope of AutoML systems. For reproducability, we release our code and a simple demo.

On the Importance of Hyperparameters and Data Augmentation for Self-Supervised Learning

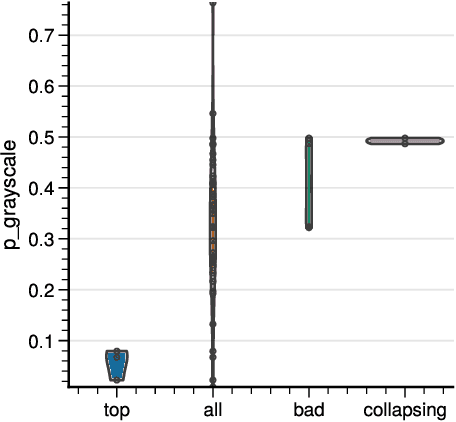
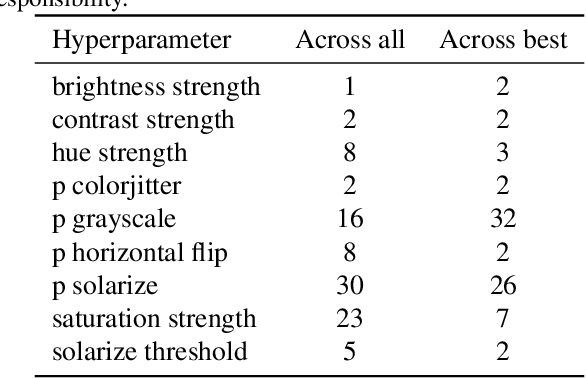
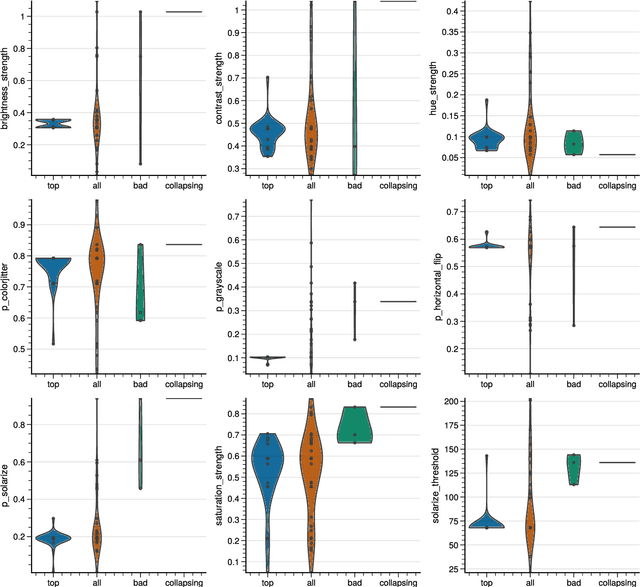
Self-Supervised Learning (SSL) has become a very active area of Deep Learning research where it is heavily used as a pre-training method for classification and other tasks. However, the rapid pace of advancements in this area comes at a price: training pipelines vary significantly across papers, which presents a potentially crucial confounding factor. Here, we show that, indeed, the choice of hyperparameters and data augmentation strategies can have a dramatic impact on performance. To shed light on these neglected factors and help maximize the power of SSL, we hyperparameterize these components and optimize them with Bayesian optimization, showing improvements across multiple datasets for the SimSiam SSL approach. Realizing the importance of data augmentations for SSL, we also introduce a new automated data augmentation algorithm, GroupAugment, which considers groups of augmentations and optimizes the sampling across groups. In contrast to algorithms designed for supervised learning, GroupAugment achieved consistently high linear evaluation accuracy across all datasets we considered. Overall, our results indicate the importance and likely underestimated role of data augmentation for SSL.