DCDILP: a distributed learning method for large-scale causal structure learning

This paper presents a novel approach to causal discovery through a divide-and-conquer framework. By decomposing the problem into smaller subproblems defined on Markov blankets, the proposed DCDILP method first explores in parallel the local causal graphs of these subproblems. However, this local discovery phase encounters systematic challenges due to the presence of hidden confounders (variables within each Markov blanket may be influenced by external variables). Moreover, aggregating these local causal graphs in a consistent global graph defines a large size combinatorial optimization problem. DCDILP addresses these challenges by: i) restricting the local subgraphs to causal links only related with the central variable of the Markov blanket; ii) formulating the reconciliation of local causal graphs as an integer linear programming method. The merits of the approach, in both terms of causal discovery accuracy and scalability in the size of the problem, are showcased by experiments and comparisons with the state of the art.

High-Dimensional Causal Discovery: Learning from Inverse Covariance via Independence-based Decomposition

Inferring causal relationships from observational data is a fundamental yet highly complex problem when the number of variables is large. Recent advances have made much progress in learning causal structure models (SEMs) but still face challenges in scalability. This paper aims to efficiently discover causal DAGs from high-dimensional data. We investigate a way of recovering causal DAGs from inverse covariance estimators of the observational data. The proposed algorithm, called ICID (inverse covariance estimation and {\it independence-based} decomposition), searches for a decomposition of the inverse covariance matrix that preserves its nonzero patterns. This algorithm benefits from properties of positive definite matrices supported on {\it chordal} graphs and the preservation of nonzero patterns in their Cholesky decomposition; we find exact mirroring between the support-preserving property and the independence-preserving property of our decomposition method, which explains its effectiveness in identifying causal structures from the data distribution. We show that the proposed algorithm recovers causal DAGs with a complexity of $O(d^2)$ in the context of sparse SEMs. The advantageously low complexity is reflected by good scalability of our algorithm in thorough experiments and comparisons with state-of-the-art algorithms.

From graphs to DAGs: a low-complexity model and a scalable algorithm

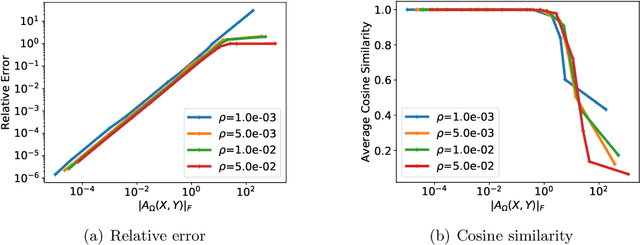
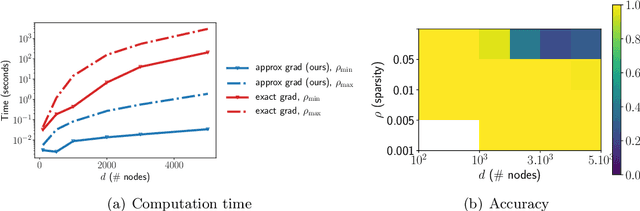
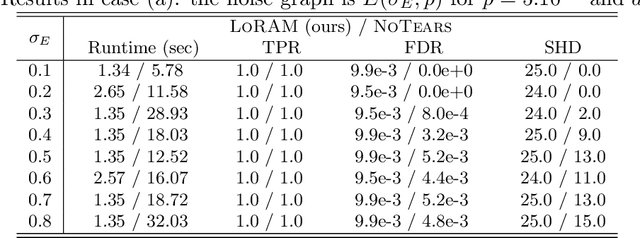
Learning directed acyclic graphs (DAGs) is long known a critical challenge at the core of probabilistic and causal modeling. The NoTears approach of (Zheng et al., 2018), through a differentiable function involving the matrix exponential trace $\mathrm{tr}(\exp(\cdot))$, opens up a way to learning DAGs via continuous optimization, though with a $O(d^3)$ complexity in the number $d$ of nodes. This paper presents a low-complexity model, called LoRAM for Low-Rank Additive Model, which combines low-rank matrix factorization with a sparsification mechanism for the continuous optimization of DAGs. The main contribution of the approach lies in an efficient gradient approximation method leveraging the low-rank property of the model, and its straightforward application to the computation of projections from graph matrices onto the DAG matrix space. The proposed method achieves a reduction from a cubic complexity to quadratic complexity while handling the same DAG characteristic function as NoTears, and scales easily up to thousands of nodes for the projection problem. The experiments show that the LoRAM achieves efficiency gains of orders of magnitude compared to the state-of-the-art at the expense of a very moderate accuracy loss in the considered range of sparse matrices, and with a low sensitivity to the rank choice of the model's low-rank component.

Frugal Machine Learning

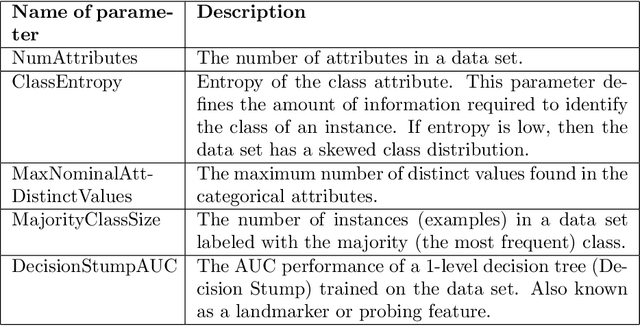
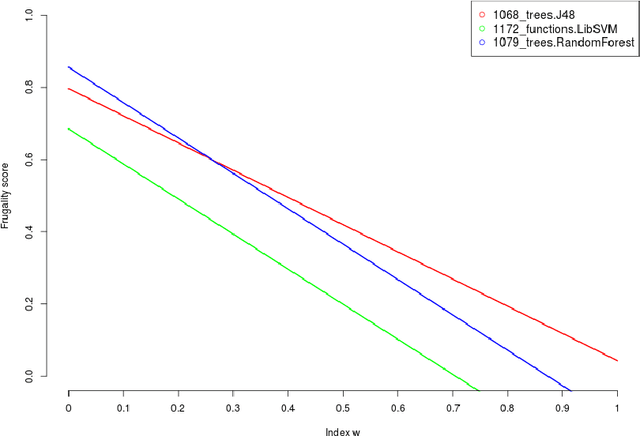
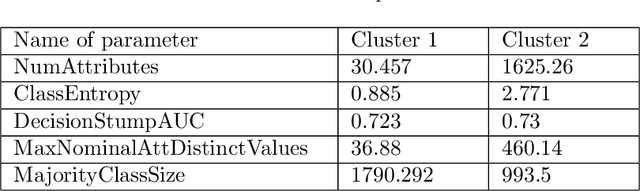
Machine learning, already at the core of increasingly many systems and applications, is set to become even more ubiquitous with the rapid rise of wearable devices and the Internet of Things. In most machine learning applications, the main focus is on the quality of the results achieved (e.g., prediction accuracy), and hence vast amounts of data are being collected, requiring significant computational resources to build models. In many scenarios, however, it is infeasible or impractical to set up large centralized data repositories. In personal health, for instance, privacy issues may inhibit the sharing of detailed personal data. In such cases, machine learning should ideally be performed on wearable devices themselves, which raises major computational limitations such as the battery capacity of smartwatches. This paper thus investigates frugal learning, aimed to build the most accurate possible models using the least amount of resources. A wide range of learning algorithms is examined through a frugal lens, analyzing their accuracy/runtime performance on a wide range of data sets. The most promising algorithms are thereafter assessed in a real-world scenario by implementing them in a smartwatch and letting them learn activity recognition models on the watch itself.

Distribution-Based Invariant Deep Networks for Learning Meta-Features

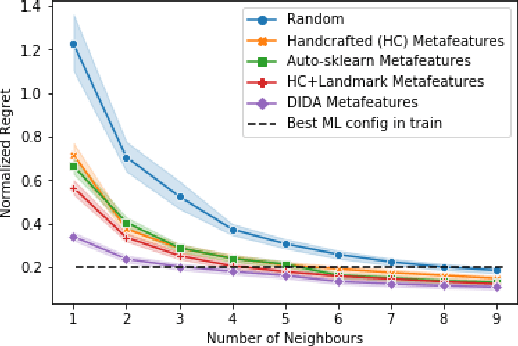
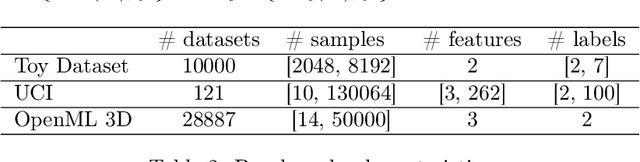
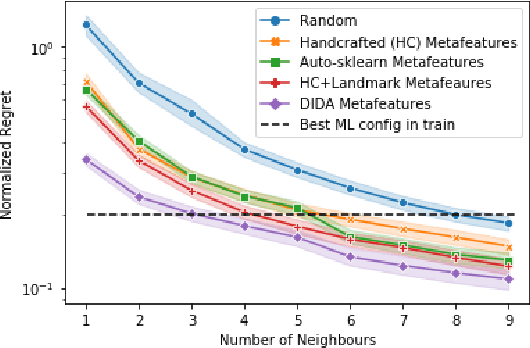
Recent advances in deep learning from probability distributions enable to achieve classification or regression from distribution samples, invariant under permutation of the samples. This paper extends the distribution-based deep neural architectures to achieve classification or regression from distribution samples, invariant under permutation of the descriptive features, too. The motivation for this extension is the Auto-ML problem, aimed to identify a priori the ML configuration best suited to a dataset. Formally, a distribution-based invariant deep learning architecture is presented, and leveraged to extract the meta-features characterizing a dataset. The contribution of the paper is twofold. On the theoretical side, the proposed architecture inherits the NN properties of universal approximation, and the robustness of the approach w.r.t. moderate perturbations is established. On the empirical side, a proof of concept of the approach is proposed, to identify the SVM hyper-parameters best suited to a large benchmark of diversified small size datasets.

Variational Auto-Encoder: not all failures are equal

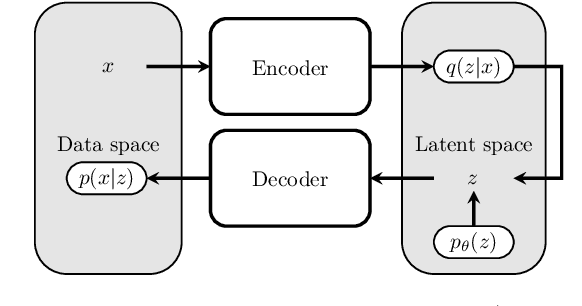
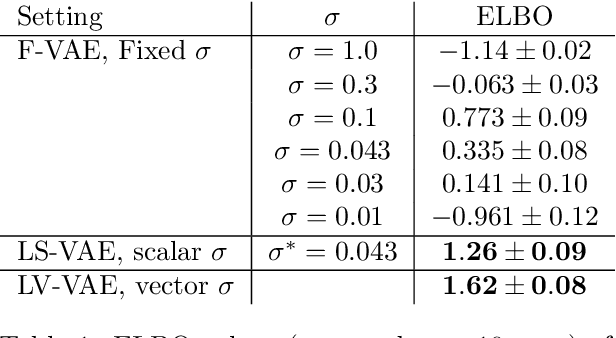
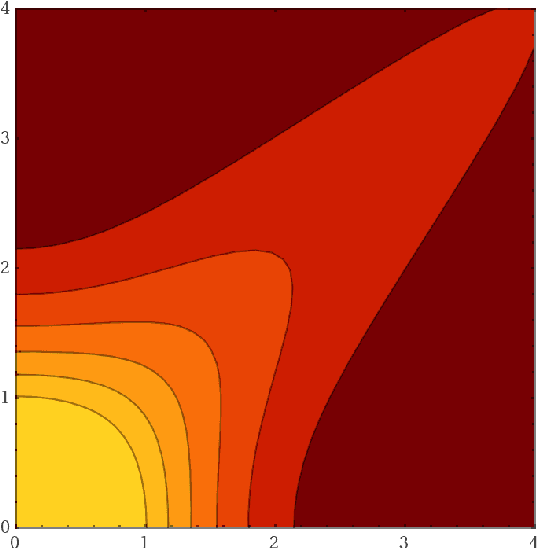
We claim that a source of severe failures for Variational Auto-Encoders is the choice of the distribution class used for the observation model.A first theoretical and experimental contribution of the paper is to establish that even in the large sample limit with arbitrarily powerful neural architectures and latent space, the VAE failsif the sharpness of the distribution class does not match the scale of the data.Our second claim is that the distribution sharpness must preferably be learned by the VAE (as opposed to, fixed and optimized offline): Autonomously adjusting this sharpness allows the VAE to dynamically control the trade-off between the optimization of the reconstruction loss and the latent compression. A second empirical contribution is to show how the control of this trade-off is instrumental in escaping poor local optima, akin a simulated annealing schedule.Both claims are backed upon experiments on artificial data, MNIST and CelebA, showing how sharpness learning addresses the notorious VAE blurriness issue.

From abstract items to latent spaces to observed data and back: Compositional Variational Auto-Encoder

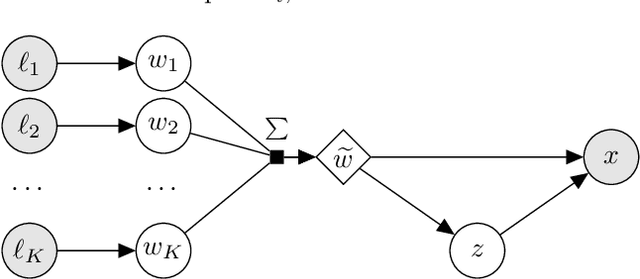
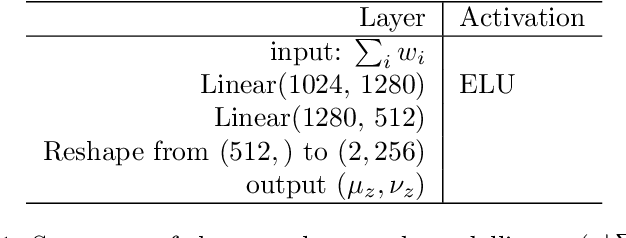
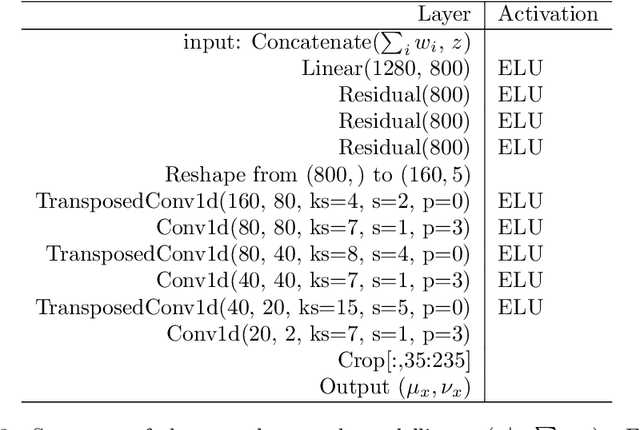
Conditional Generative Models are now acknowledged an essential tool in Machine Learning. This paper focuses on their control. While many approaches aim at disentangling the data through the coordinate-wise control of their latent representations, another direction is explored in this paper. The proposed CompVAE handles data with a natural multi-ensemblist structure (i.e. that can naturally be decomposed into elements). Derived from Bayesian variational principles, CompVAE learns a latent representation leveraging both observational and symbolic information. A first contribution of the approach is that this latent representation supports a compositional generative model, amenable to multi-ensemblist operations (addition or subtraction of elements in the composition). This compositional ability is enabled by the invariance and generality of the whole framework w.r.t. respectively, the order and number of the elements. The second contribution of the paper is a proof of concept on synthetic 1D and 2D problems, demonstrating the efficiency of the proposed approach.

Automated Machine Learning with Monte-Carlo Tree Search (Extended Version)

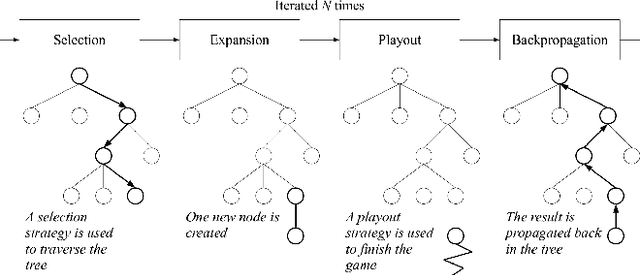
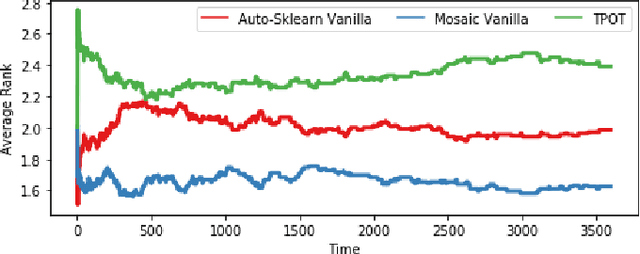
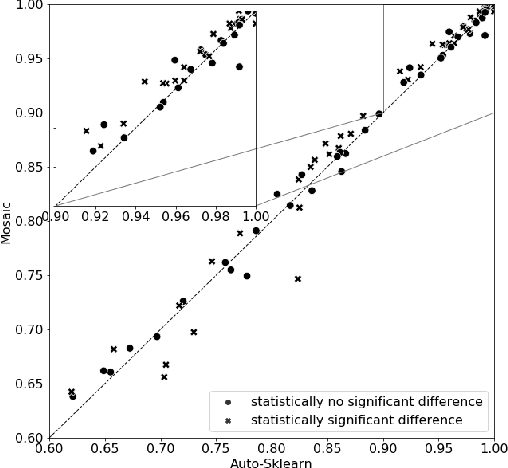
The AutoML task consists of selecting the proper algorithm in a machine learning portfolio, and its hyperparameter values, in order to deliver the best performance on the dataset at hand. Mosaic, a Monte-Carlo tree search (MCTS) based approach, is presented to handle the AutoML hybrid structural and parametric expensive black-box optimization problem. Extensive empirical studies are conducted to independently assess and compare: i) the optimization processes based on Bayesian optimization or MCTS; ii) its warm-start initialization; iii) the ensembling of the solutions gathered along the search. Mosaic is assessed on the OpenML 100 benchmark and the Scikit-learn portfolio, with statistically significant gains over Auto-Sklearn, winner of former international AutoML challenges.

New Losses for Generative Adversarial Learning

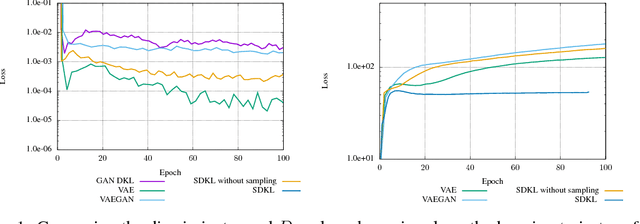
Generative Adversarial Networks (Goodfellow et al., 2014), a major breakthrough in the field of generative modeling, learn a discriminator to estimate some distance between the target and the candidate distributions. This paper examines mathematical issues regarding the way the gradients for the generative model are computed in this context, and notably how to take into account how the discriminator itself depends on the generator parameters. A unifying methodology is presented to define mathematically sound training objectives for generative models taking this dependency into account in a robust way, covering both GAN, VAE and some GAN variants as particular cases.

SAM: Structural Agnostic Model, Causal Discovery and Penalized Adversarial Learning

We present the Structural Agnostic Model (SAM), a framework to estimate end-to-end non-acyclic causal graphs from observational data. In a nutshell, SAM implements an adversarial game in which a separate model generates each variable, given real values from all others. In tandem, a discriminator attempts to distinguish between the joint distributions of real and generated samples. Finally, a sparsity penalty forces each generator to consider only a small subset of the variables, yielding a sparse causal graph. SAM scales easily to hundreds variables. Our experiments show the state-of-the-art performance of SAM on discovering causal structures and modeling interventions, in both acyclic and non-acyclic graphs.