Boltzmann Tuning of Generative Models

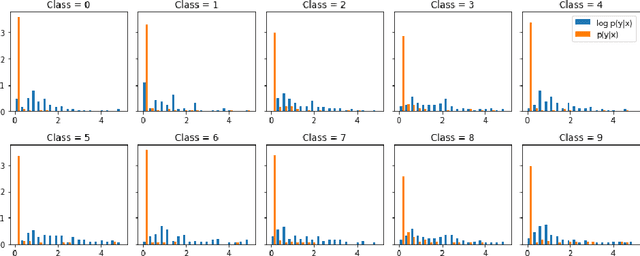
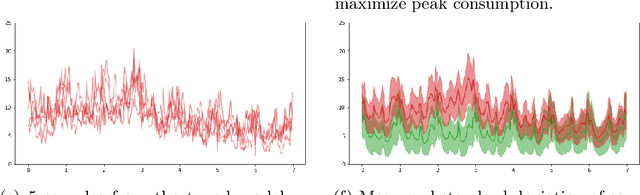
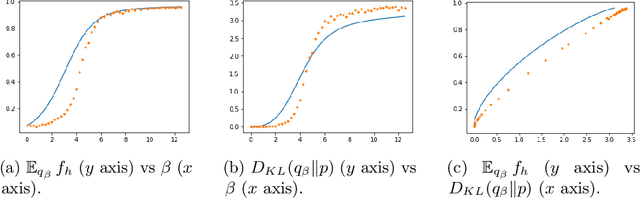
The paper focuses on the a posteriori tuning of a generative model in order to favor the generation of good instances in the sense of some external differentiable criterion. The proposed approach, called Boltzmann Tuning of Generative Models (BTGM), applies to a wide range of applications. It covers conditional generative modelling as a particular case, and offers an affordable alternative to rejection sampling. The contribution of the paper is twofold. Firstly, the objective is formalized and tackled as a well-posed optimization problem; a practical methodology is proposed to choose among the candidate criteria representing the same goal, the one best suited to efficiently learn a tuned generative model. Secondly, the merits of the approach are demonstrated on a real-world application, in the context of robust design for energy policies, showing the ability of BTGM to sample the extreme regions of the considered criteria.

Variational Auto-Encoder: not all failures are equal

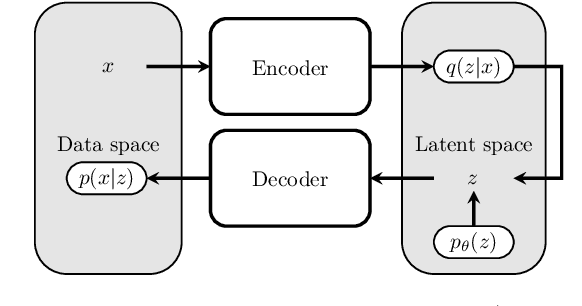
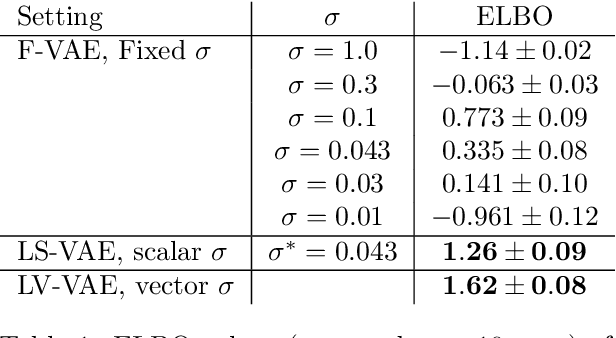
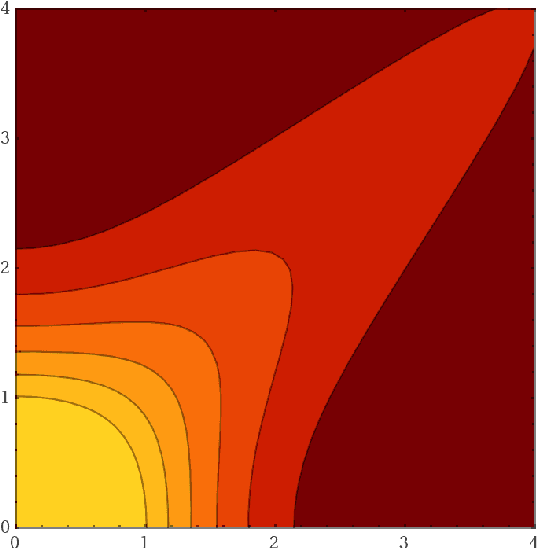
We claim that a source of severe failures for Variational Auto-Encoders is the choice of the distribution class used for the observation model.A first theoretical and experimental contribution of the paper is to establish that even in the large sample limit with arbitrarily powerful neural architectures and latent space, the VAE failsif the sharpness of the distribution class does not match the scale of the data.Our second claim is that the distribution sharpness must preferably be learned by the VAE (as opposed to, fixed and optimized offline): Autonomously adjusting this sharpness allows the VAE to dynamically control the trade-off between the optimization of the reconstruction loss and the latent compression. A second empirical contribution is to show how the control of this trade-off is instrumental in escaping poor local optima, akin a simulated annealing schedule.Both claims are backed upon experiments on artificial data, MNIST and CelebA, showing how sharpness learning addresses the notorious VAE blurriness issue.

Towards AutoML in the presence of Drift: first results

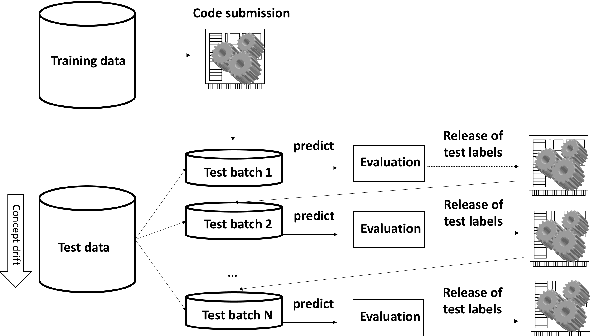
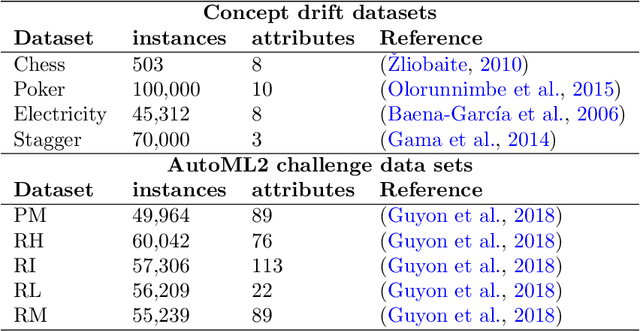
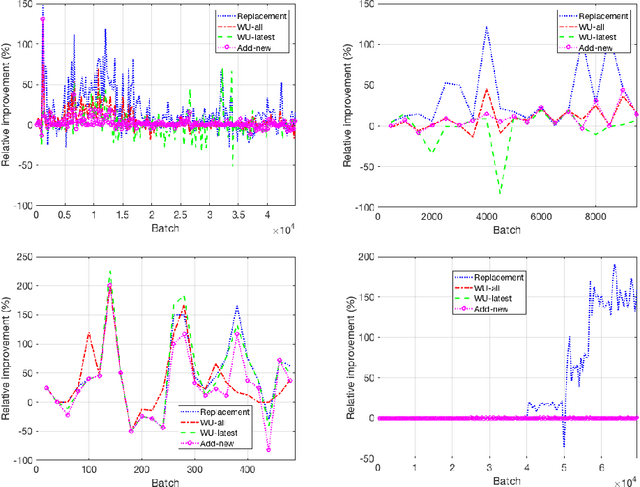
Research progress in AutoML has lead to state of the art solutions that can cope quite wellwith supervised learning task, e.g., classification with AutoSklearn. However, so far thesesystems do not take into account the changing nature of evolving data over time (i.e., theystill assume i.i.d. data); even when this sort of domains are increasingly available in realapplications (e.g., spam filtering, user preferences, etc.). We describe a first attempt to de-velop an AutoML solution for scenarios in which data distribution changes relatively slowlyover time and in which the problem is approached in a lifelong learning setting. We extendAuto-Sklearn with sound and intuitive mechanisms that allow it to cope with this sort ofproblems. The extended Auto-Sklearn is combined with concept drift detection techniquesthat allow it to automatically determine when the initial models have to be adapted. Wereport experimental results in benchmark data from AutoML competitions that adhere tothis scenario. Results demonstrate the effectiveness of the proposed methodology.

Multi-Domain Adversarial Learning

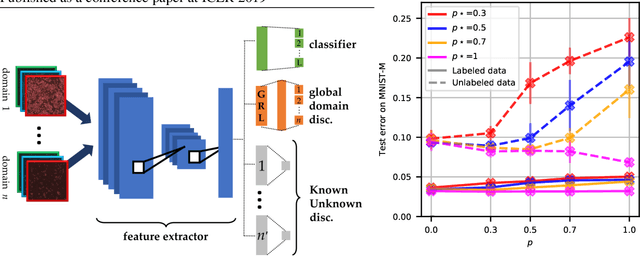
Multi-domain learning (MDL) aims at obtaining a model with minimal average risk across multiple domains. Our empirical motivation is automated microscopy data, where cultured cells are imaged after being exposed to known and unknown chemical perturbations, and each dataset displays significant experimental bias. This paper presents a multi-domain adversarial learning approach, MuLANN, to leverage multiple datasets with overlapping but distinct class sets, in a semi-supervised setting. Our contributions include: i) a bound on the average- and worst-domain risk in MDL, obtained using the H-divergence; ii) a new loss to accommodate semi-supervised multi-domain learning and domain adaptation; iii) the experimental validation of the approach, improving on the state of the art on two standard image benchmarks, and a novel bioimage dataset, Cell.

Toward Optimal Run Racing: Application to Deep Learning Calibration

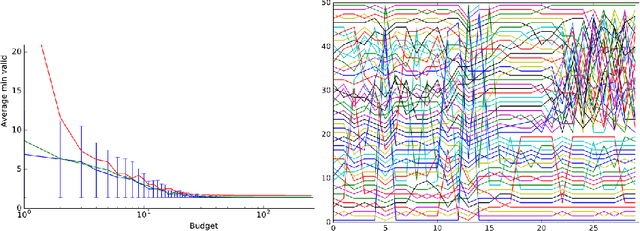
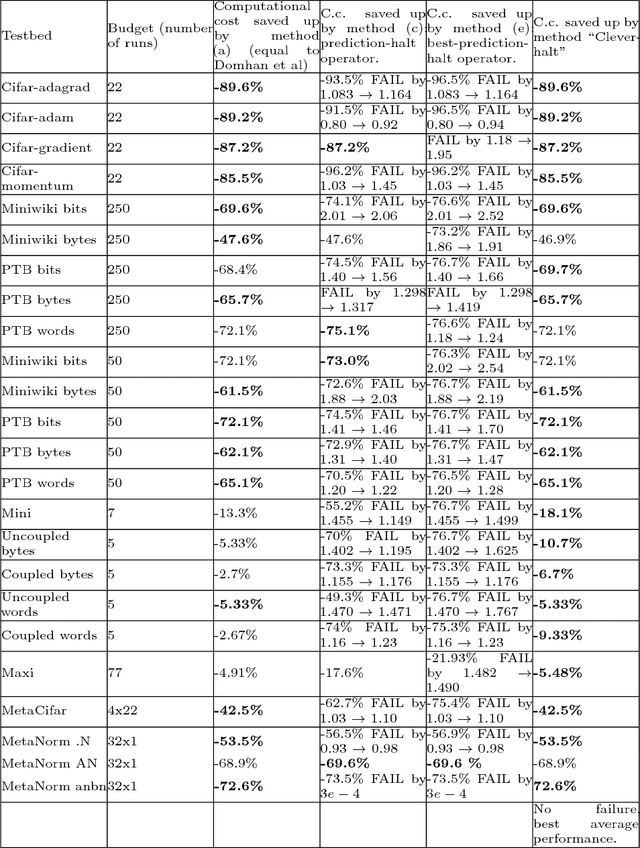
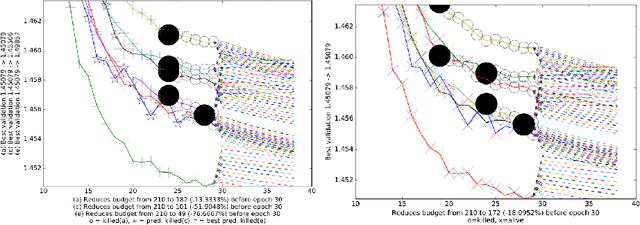
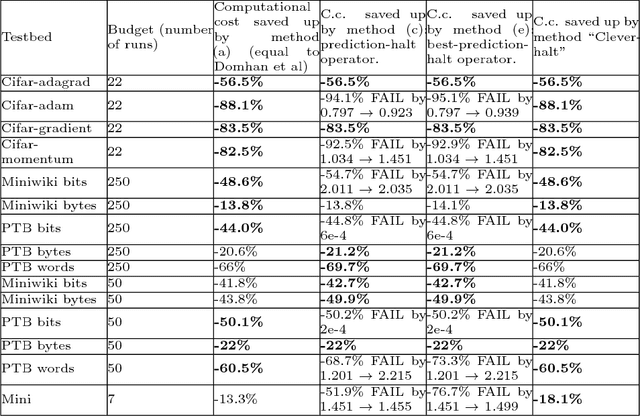
This paper aims at one-shot learning of deep neural nets, where a highly parallel setting is considered to address the algorithm calibration problem - selecting the best neural architecture and learning hyper-parameter values depending on the dataset at hand. The notoriously expensive calibration problem is optimally reduced by detecting and early stopping non-optimal runs. The theoretical contribution regards the optimality guarantees within the multiple hypothesis testing framework. Experimentations on the Cifar10, PTB and Wiki benchmarks demonstrate the relevance of the approach with a principled and consistent improvement on the state of the art with no extra hyper-parameter.

Scaling Analysis of Affinity Propagation

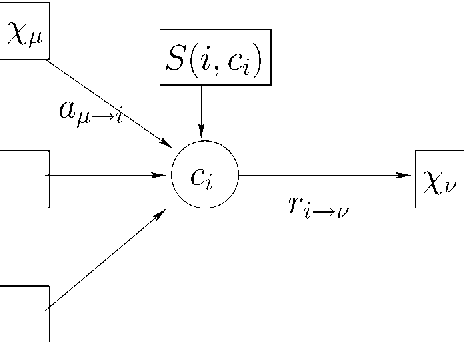
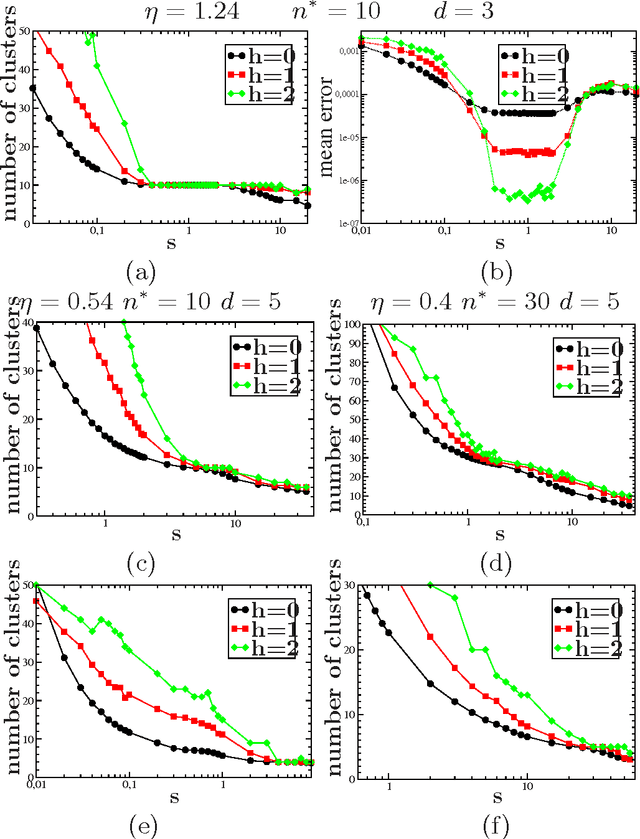
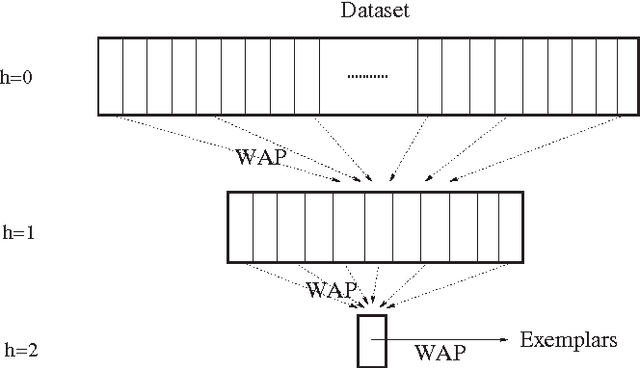
We analyze and exploit some scaling properties of the Affinity Propagation (AP) clustering algorithm proposed by Frey and Dueck (2007). First we observe that a divide and conquer strategy, used on a large data set hierarchically reduces the complexity ${\cal O}(N^2)$ to ${\cal O}(N^{(h+2)/(h+1)})$, for a data-set of size $N$ and a depth $h$ of the hierarchical strategy. For a data-set embedded in a $d$-dimensional space, we show that this is obtained without notably damaging the precision except in dimension $d=2$. In fact, for $d$ larger than 2 the relative loss in precision scales like $N^{(2-d)/(h+1)d}$. Finally, under some conditions we observe that there is a value $s^*$ of the penalty coefficient, a free parameter used to fix the number of clusters, which separates a fragmentation phase (for $s<s^*$) from a coalescent one (for $s>s^*$) of the underlying hidden cluster structure. At this precise point holds a self-similarity property which can be exploited by the hierarchical strategy to actually locate its position. From this observation, a strategy based on \AP can be defined to find out how many clusters are present in a given dataset.