Provably Safeguarding a Classifier from OOD and Adversarial Samples: an Extreme Value Theory Approach

This paper introduces a novel method, Sample-efficient Probabilistic Detection using Extreme Value Theory (SPADE), which transforms a classifier into an abstaining classifier, offering provable protection against out-of-distribution and adversarial samples. The approach is based on a Generalized Extreme Value (GEV) model of the training distribution in the classifier's latent space, enabling the formal characterization of OOD samples. Interestingly, under mild assumptions, the GEV model also allows for formally characterizing adversarial samples. The abstaining classifier, which rejects samples based on their assessment by the GEV model, provably avoids OOD and adversarial samples. The empirical validation of the approach, conducted on various neural architectures (ResNet, VGG, and Vision Transformer) and medium and large-sized datasets (CIFAR-10, CIFAR-100, and ImageNet), demonstrates its frugality, stability, and efficiency compared to the state of the art.

Exponentially fast convergence to (strict) equilibrium via hedging

Motivated by applications to data networks where fast convergence is essential, we analyze the problem of learning in generic N-person games that admit a Nash equilibrium in pure strategies. Specifically, we consider a scenario where players interact repeatedly and try to learn from past experience by small adjustments based on local - and possibly imperfect - payoff information. For concreteness, we focus on the so-called "hedge" variant of the exponential weights algorithm where players select an action with probability proportional to the exponential of the action's cumulative payoff over time. When players have perfect information on their mixed payoffs, the algorithm converges locally to a strict equilibrium and the rate of convergence is exponentially fast - of the order of $\mathcal{O}(\exp(-a\sum_{j=1}^{t}\gamma_{j}))$ where $a>0$ is a constant and $\gamma_{j}$ is the algorithm's step-size. In the presence of uncertainty, convergence requires a more conservative step-size policy, but with high probability, the algorithm remains locally convergent and achieves an exponential convergence rate.

File Transfer Application For Sharing Femto Access

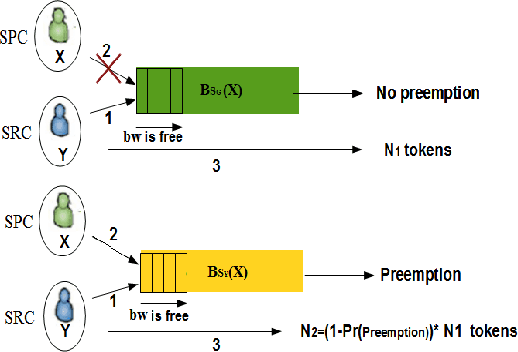
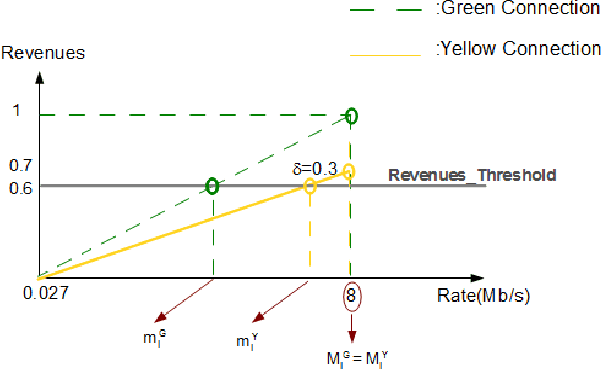
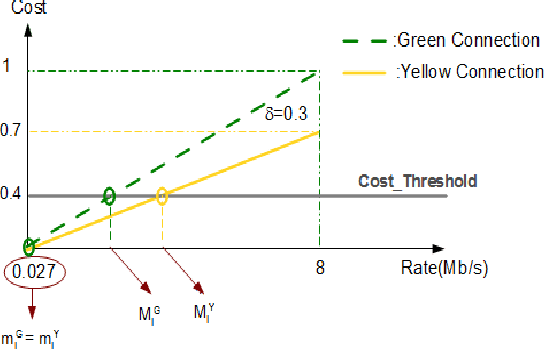
In wireless access network optimization, today's main challenges reside in traffic offload and in the improvement of both capacity and coverage networks. The operators are interested in solving their localized coverage and capacity problems in areas where the macro network signal is not able to serve the demand for mobile data. Thus, the major issue for operators is to find the best solution at reasonable expanses. The femto cell seems to be the answer to this problematic. In this work (This work is supported by the COMET project AWARE. http://www.ftw.at/news/project-start-for-aware-ftw), we focus on the problem of sharing femto access between a same mobile operator's customers. This problem can be modeled as a game where service requesters customers (SRCs) and service providers customers (SPCs) are the players. This work addresses the sharing femto access problem considering only one SPC using game theory tools. We consider that SRCs are static and have some similar and regular connection behavior. We also note that the SPC and each SRC have a software embedded respectively on its femto access, user equipment (UE). After each connection requested by a SRC, its software will learn the strategy increasing its gain knowing that no information about the other SRCs strategies is given. The following article presents a distributed learning algorithm with incomplete information running in SRCs software. We will then answer the following questions for a game with $N$ SRCs and one SPC: how many connections are necessary for each SRC in order to learn the strategy maximizing its gain? Does this algorithm converge to a stable state? If yes, does this state a Nash Equilibrium and is there any way to optimize the learning process duration time triggered by SRCs software?

Learning Equilibria in Games by Stochastic Distributed Algorithms

We consider a class of fully stochastic and fully distributed algorithms, that we prove to learn equilibria in games. Indeed, we consider a family of stochastic distributed dynamics that we prove to converge weakly (in the sense of weak convergence for probabilistic processes) towards their mean-field limit, i.e an ordinary differential equation (ODE) in the general case. We focus then on a class of stochastic dynamics where this ODE turns out to be related to multipopulation replicator dynamics. Using facts known about convergence of this ODE, we discuss the convergence of the initial stochastic dynamics: For general games, there might be non-convergence, but when convergence of the ODE holds, considered stochastic algorithms converge towards Nash equilibria. For games admitting Lyapunov functions, that we call Lyapunov games, the stochastic dynamics converge. We prove that any ordinal potential game, and hence any potential game is a Lyapunov game, with a multiaffine Lyapunov function. For Lyapunov games with a multiaffine Lyapunov function, we prove that this Lyapunov function is a super-martingale over the stochastic dynamics. This leads a way to provide bounds on their time of convergence by martingale arguments. This applies in particular for many classes of games that have been considered in literature, including several load balancing game scenarios and congestion games.