Ministral 3

We introduce the Ministral 3 series, a family of parameter-efficient dense language models designed for compute and memory constrained applications, available in three model sizes: 3B, 8B, and 14B parameters. For each model size, we release three variants: a pretrained base model for general-purpose use, an instruction finetuned, and a reasoning model for complex problem-solving. In addition, we present our recipe to derive the Ministral 3 models through Cascade Distillation, an iterative pruning and continued training with distillation technique. Each model comes with image understanding capabilities, all under the Apache 2.0 license.

Evaluation of retrieval-based QA on QUEST-LOFT

Despite the popularity of retrieval-augmented generation (RAG) as a solution for grounded QA in both academia and industry, current RAG methods struggle with questions where the necessary information is distributed across many documents or where retrieval needs to be combined with complex reasoning. Recently, the LOFT study has shown that this limitation also applies to approaches based on long-context language models, with the QUEST benchmark exhibiting particularly large headroom. In this paper, we provide an in-depth analysis of the factors contributing to the poor performance on QUEST-LOFT, publish updated numbers based on a thorough human evaluation, and demonstrate that RAG can be optimized to significantly outperform long-context approaches when combined with a structured output format containing reasoning and evidence, optionally followed by answer re-verification.

Differentially-Private Bayes Consistency

We construct a universally Bayes consistent learning rule that satisfies differential privacy (DP). We first handle the setting of binary classification and then extend our rule to the more general setting of density estimation (with respect to the total variation metric). The existence of a universally consistent DP learner reveals a stark difference with the distribution-free PAC model. Indeed, in the latter DP learning is extremely limited: even one-dimensional linear classifiers are not privately learnable in this stringent model. Our result thus demonstrates that by allowing the learning rate to depend on the target distribution, one can circumvent the above-mentioned impossibility result and in fact, learn \emph{arbitrary} distributions by a single DP algorithm. As an application, we prove that any VC class can be privately learned in a semi-supervised setting with a near-optimal \emph{labeled} sample complexity of $\tilde{O}(d/\varepsilon)$ labeled examples (and with an unlabeled sample complexity that can depend on the target distribution).

The Dynamics of Sharpness-Aware Minimization: Bouncing Across Ravines and Drifting Towards Wide Minima

We consider Sharpness-Aware Minimization (SAM), a gradient-based optimization method for deep networks that has exhibited performance improvements on image and language prediction problems. We show that when SAM is applied with a convex quadratic objective, for most random initializations it converges to a cycle that oscillates between either side of the minimum in the direction with the largest curvature, and we provide bounds on the rate of convergence. In the non-quadratic case, we show that such oscillations effectively perform gradient descent, with a smaller step-size, on the spectral norm of the Hessian. In such cases, SAM's update may be regarded as a third derivative -- the derivative of the Hessian in the leading eigenvector direction -- that encourages drift toward wider minima.

Compositional Semantic Parsing with Large Language Models

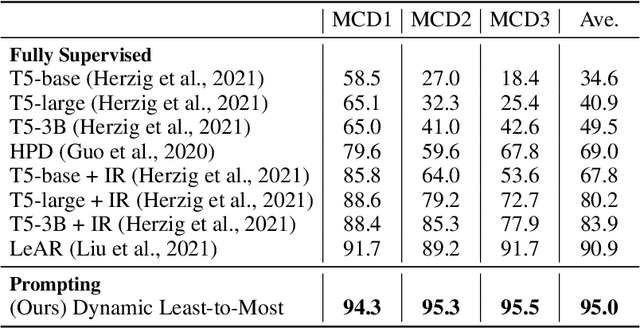
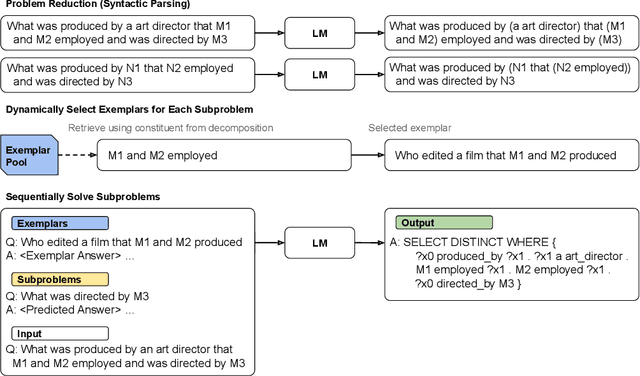
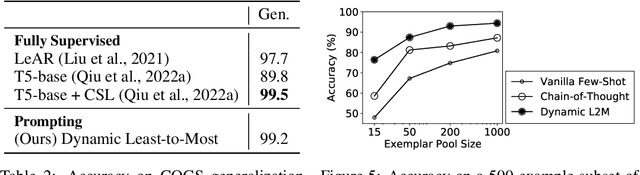
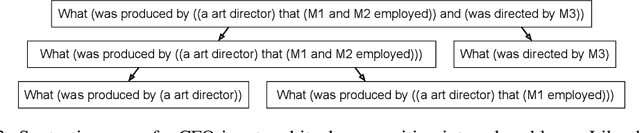
Humans can reason compositionally when presented with new tasks. Previous research shows that appropriate prompting techniques enable large language models (LLMs) to solve artificial compositional generalization tasks such as SCAN. In this work, we identify additional challenges in more realistic semantic parsing tasks with larger vocabulary and refine these prompting techniques to address them. Our best method is based on least-to-most prompting: it decomposes the problem using prompting-based syntactic parsing, then uses this decomposition to select appropriate exemplars and to sequentially generate the semantic parse. This method allows us to set a new state of the art for CFQ while requiring only 1% of the training data used by traditional approaches. Due to the general nature of our approach, we expect similar efforts will lead to new results in other tasks and domains, especially for knowledge-intensive applications.

Fine-Grained Distribution-Dependent Learning Curves

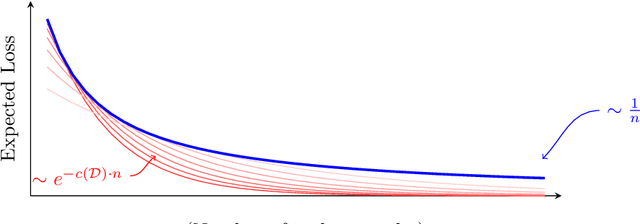
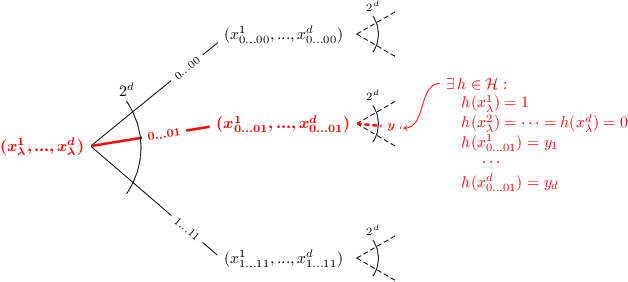
Learning curves plot the expected error of a learning algorithm as a function of the number of labeled input samples. They are widely used by machine learning practitioners as a measure of an algorithm's performance, but classic PAC learning theory cannot explain their behavior. In this paper we introduce a new combinatorial characterization called the VCL dimension that improves and refines the recent results of Bousquet et al. (2021). Our characterization sheds new light on the structure of learning curves by providing fine-grained bounds, and showing that for classes with finite VCL, the rate of decay can be decomposed into a linear component that depends only on the hypothesis class and an exponential component that depends also on the target distribution. In particular, the finer nuance of the VCL dimension implies lower bounds that are quantitatively stronger than the bounds of Bousquet et al. (2021) and qualitatively stronger than classic 'no free lunch' lower bounds. The VCL characterization solves an open problem studied by Antos and Lugosi (1998), who asked in what cases such lower bounds exist. As a corollary, we recover their lower bound for half-spaces in $\mathbb{R}^d$, and we do so in a principled way that should be applicable to other cases as well. Finally, to provide another viewpoint on our work and how it compares to traditional PAC learning bounds, we also present an alternative formulation of our results in a language that is closer to the PAC setting.

Least-to-Most Prompting Enables Complex Reasoning in Large Language Models

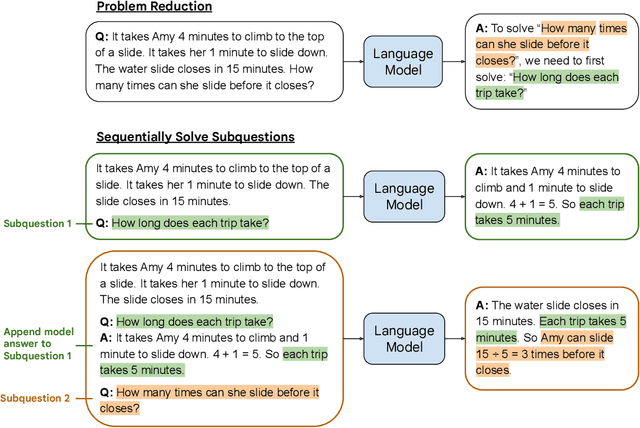
We propose a novel prompting strategy, least-to-most prompting, that enables large language models to better perform multi-step reasoning tasks. Least-to-most prompting first reduces a complex problem into a list of subproblems, and then sequentially solves the subproblems, whereby solving a given subproblem is facilitated by the model's answers to previously solved subproblems. Experiments on symbolic manipulation, compositional generalization and numerical reasoning demonstrate that least-to-most prompting can generalize to examples that are harder than those seen in the prompt context, outperforming other prompting-based approaches by a large margin. A notable empirical result is that the GPT-3 code-davinci-002 model with least-to-most-prompting can solve the SCAN benchmark with an accuracy of 99.7% using 14 examples. As a comparison, the neural-symbolic models in the literature specialized for solving SCAN are trained with the full training set of more than 15,000 examples.

Monotone Learning

The amount of training-data is one of the key factors which determines the generalization capacity of learning algorithms. Intuitively, one expects the error rate to decrease as the amount of training-data increases. Perhaps surprisingly, natural attempts to formalize this intuition give rise to interesting and challenging mathematical questions. For example, in their classical book on pattern recognition, Devroye, Gyorfi, and Lugosi (1996) ask whether there exists a {monotone} Bayes-consistent algorithm. This question remained open for over 25 years, until recently Pestov (2021) resolved it for binary classification, using an intricate construction of a monotone Bayes-consistent algorithm. We derive a general result in multiclass classification, showing that every learning algorithm A can be transformed to a monotone one with similar performance. Further, the transformation is efficient and only uses a black-box oracle access to A. This demonstrates that one can provably avoid non-monotonic behaviour without compromising performance, thus answering questions asked by Devroye et al (1996), Viering, Mey, and Loog (2019), Viering and Loog (2021), and by Mhammedi (2021). Our transformation readily implies monotone learners in a variety of contexts: for example it extends Pestov's result to classification tasks with an arbitrary number of labels. This is in contrast with Pestov's work which is tailored to binary classification. In addition, we provide uniform bounds on the error of the monotone algorithm. This makes our transformation applicable in distribution-free settings. For example, in PAC learning it implies that every learnable class admits a monotone PAC learner. This resolves questions by Viering, Mey, and Loog (2019); Viering and Loog (2021); Mhammedi (2021).

Statistically Near-Optimal Hypothesis Selection

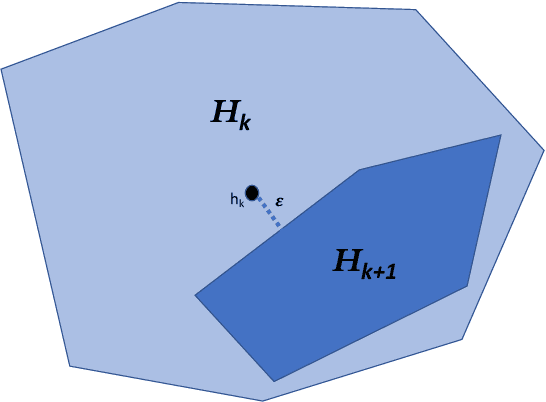
Hypothesis Selection is a fundamental distribution learning problem where given a comparator-class $Q=\{q_1,\ldots, q_n\}$ of distributions, and a sampling access to an unknown target distribution $p$, the goal is to output a distribution $q$ such that $\mathsf{TV}(p,q)$ is close to $opt$, where $opt = \min_i\{\mathsf{TV}(p,q_i)\}$ and $\mathsf{TV}(\cdot, \cdot)$ denotes the total-variation distance. Despite the fact that this problem has been studied since the 19th century, its complexity in terms of basic resources, such as number of samples and approximation guarantees, remains unsettled (this is discussed, e.g., in the charming book by Devroye and Lugosi `00). This is in stark contrast with other (younger) learning settings, such as PAC learning, for which these complexities are well understood. We derive an optimal $2$-approximation learning strategy for the Hypothesis Selection problem, outputting $q$ such that $\mathsf{TV}(p,q) \leq2 \cdot opt + \eps$, with a (nearly) optimal sample complexity of~$\tilde O(\log n/\epsilon^2)$. This is the first algorithm that simultaneously achieves the best approximation factor and sample complexity: previously, Bousquet, Kane, and Moran (COLT `19) gave a learner achieving the optimal $2$-approximation, but with an exponentially worse sample complexity of $\tilde O(\sqrt{n}/\epsilon^{2.5})$, and Yatracos~(Annals of Statistics `85) gave a learner with optimal sample complexity of $O(\log n /\epsilon^2)$ but with a sub-optimal approximation factor of $3$.

A Theory of Universal Learning

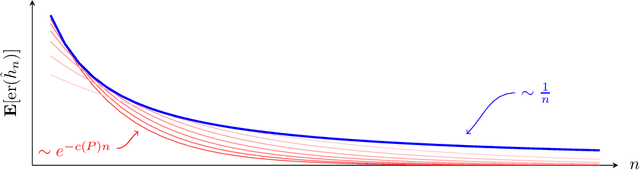
How quickly can a given class of concepts be learned from examples? It is common to measure the performance of a supervised machine learning algorithm by plotting its "learning curve", that is, the decay of the error rate as a function of the number of training examples. However, the classical theoretical framework for understanding learnability, the PAC model of Vapnik-Chervonenkis and Valiant, does not explain the behavior of learning curves: the distribution-free PAC model of learning can only bound the upper envelope of the learning curves over all possible data distributions. This does not match the practice of machine learning, where the data source is typically fixed in any given scenario, while the learner may choose the number of training examples on the basis of factors such as computational resources and desired accuracy. In this paper, we study an alternative learning model that better captures such practical aspects of machine learning, but still gives rise to a complete theory of the learnable in the spirit of the PAC model. More precisely, we consider the problem of universal learning, which aims to understand the performance of learning algorithms on every data distribution, but without requiring uniformity over the distribution. The main result of this paper is a remarkable trichotomy: there are only three possible rates of universal learning. More precisely, we show that the learning curves of any given concept class decay either at an exponential, linear, or arbitrarily slow rates. Moreover, each of these cases is completely characterized by appropriate combinatorial parameters, and we exhibit optimal learning algorithms that achieve the best possible rate in each case. For concreteness, we consider in this paper only the realizable case, though analogous results are expected to extend to more general learning scenarios.