Deep Learning Through the Lens of Example Difficulty

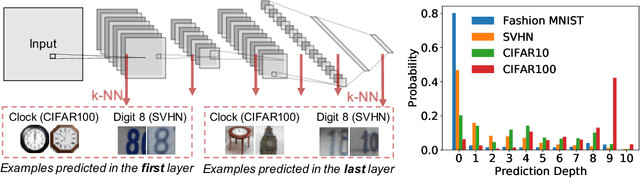
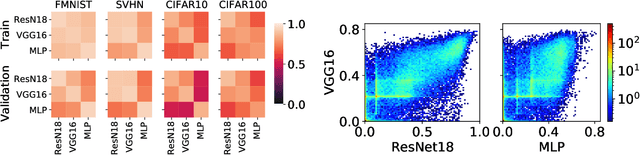
Existing work on understanding deep learning often employs measures that compress all data-dependent information into a few numbers. In this work, we adopt a perspective based on the role of individual examples. We introduce a measure of the computational difficulty of making a prediction for a given input: the (effective) prediction depth. Our extensive investigation reveals surprising yet simple relationships between the prediction depth of a given input and the model's uncertainty, confidence, accuracy and speed of learning for that data point. We further categorize difficult examples into three interpretable groups, demonstrate how these groups are processed differently inside deep models and showcase how this understanding allows us to improve prediction accuracy. Insights from our study lead to a coherent view of a number of separately reported phenomena in the literature: early layers generalize while later layers memorize; early layers converge faster and networks learn easy data and simple functions first.

What Do Neural Networks Learn When Trained With Random Labels?

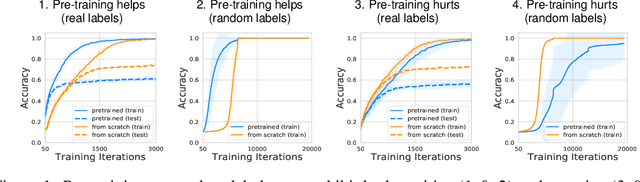
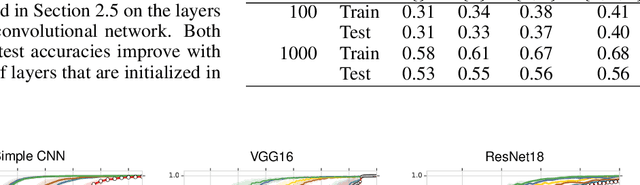
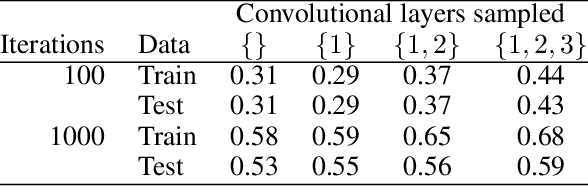
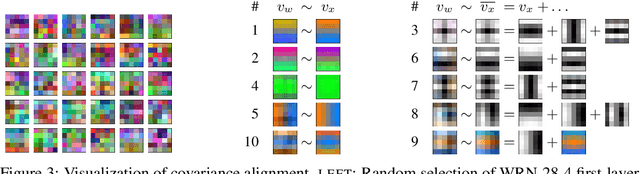
We study deep neural networks (DNNs) trained on natural image data with entirely random labels. Despite its popularity in the literature, where it is often used to study memorization, generalization, and other phenomena, little is known about what DNNs learn in this setting. In this paper, we show analytically for convolutional and fully connected networks that an alignment between the principal components of network parameters and data takes place when training with random labels. We study this alignment effect by investigating neural networks pre-trained on randomly labelled image data and subsequently fine-tuned on disjoint datasets with random or real labels. We show how this alignment produces a positive transfer: networks pre-trained with random labels train faster downstream compared to training from scratch even after accounting for simple effects, such as weight scaling. We analyze how competing effects, such as specialization at later layers, may hide the positive transfer. These effects are studied in several network architectures, including VGG16 and ResNet18, on CIFAR10 and ImageNet.

Bayesian Neural Networks at Finite Temperature

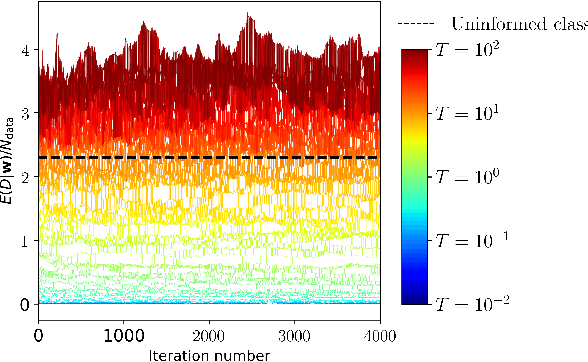
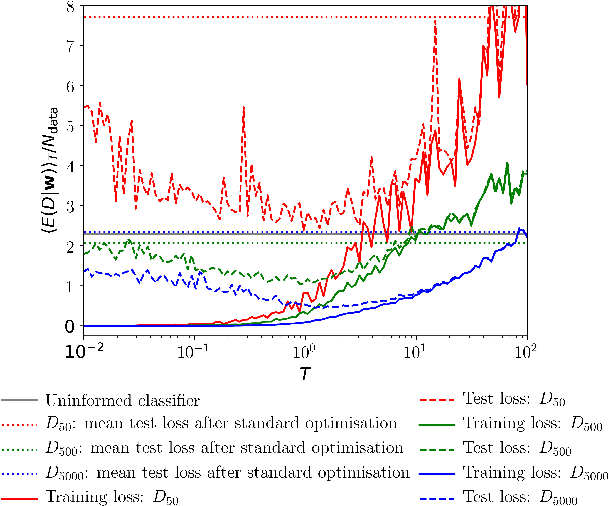
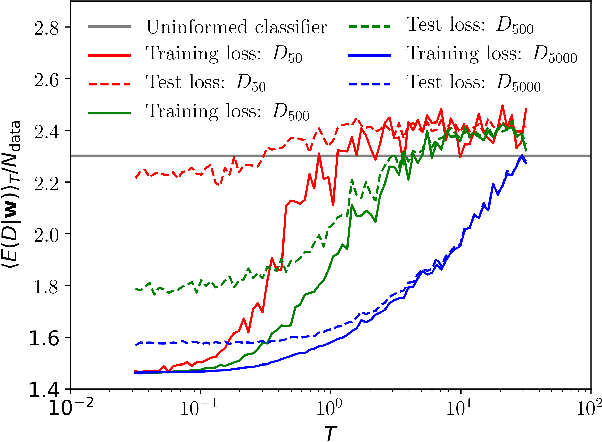
We recapitulate the Bayesian formulation of neural network based classifiers and show that, while sampling from the posterior does indeed lead to better generalisation than is obtained by standard optimisation of the cost function, even better performance can in general be achieved by sampling finite temperature ($T$) distributions derived from the posterior. Taking the example of two different deep (3 hidden layers) classifiers for MNIST data, we find quite different $T$ values to be appropriate in each case. In particular, for a typical neural network classifier a clear minimum of the test error is observed at $T>0$. This suggests an early stopping criterion for full batch simulated annealing: cool until the average validation error starts to increase, then revert to the parameters with the lowest validation error. As $T$ is increased classifiers transition from accurate classifiers to classifiers that have higher training error than assigning equal probability to each class. Efficient studies of these temperature-induced effects are enabled using a replica-exchange Hamiltonian Monte Carlo simulation technique. Finally, we show how thermodynamic integration can be used to perform model selection for deep neural networks. Similar to the Laplace approximation, this approach assumes that the posterior is dominated by a single mode. Crucially, however, no assumption is made about the shape of that mode and it is not required to precisely compute and invert the Hessian.