Machine learning Hubbard parameters with equivariant neural networks

Density-functional theory with extended Hubbard functionals (DFT+$U$+$V$) provides a robust framework to accurately describe complex materials containing transition-metal or rare-earth elements. It does so by mitigating self-interaction errors inherent to semi-local functionals which are particularly pronounced in systems with partially-filled $d$ and $f$ electronic states. However, achieving accuracy in this approach hinges upon the accurate determination of the on-site $U$ and inter-site $V$ Hubbard parameters. In practice, these are obtained either by semi-empirical tuning, requiring prior knowledge, or, more correctly, by using predictive but expensive first-principles calculations. Here, we present a machine learning model based on equivariant neural networks which uses atomic occupation matrices as descriptors, directly capturing the electronic structure, local chemical environment, and oxidation states of the system at hand. We target here the prediction of Hubbard parameters computed self-consistently with iterative linear-response calculations, as implemented in density-functional perturbation theory (DFPT), and structural relaxations. Remarkably, when trained on data from 11 materials spanning various crystal structures and compositions, our model achieves mean absolute relative errors of 3% and 5% for Hubbard $U$ and $V$ parameters, respectively. By circumventing computationally expensive DFT or DFPT self-consistent protocols, our model significantly expedites the prediction of Hubbard parameters with negligible computational overhead, while approaching the accuracy of DFPT. Moreover, owing to its robust transferability, the model facilitates accelerated materials discovery and design via high-throughput calculations, with relevance for various technological applications.

Bayesian Neural Networks at Finite Temperature

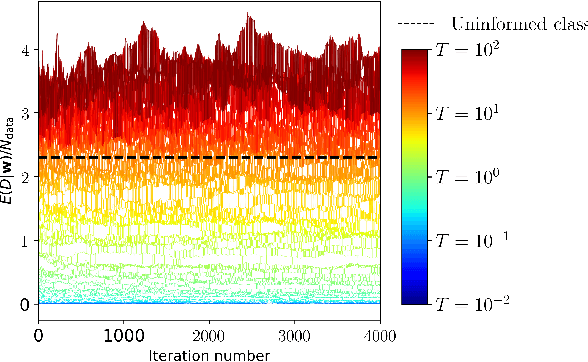
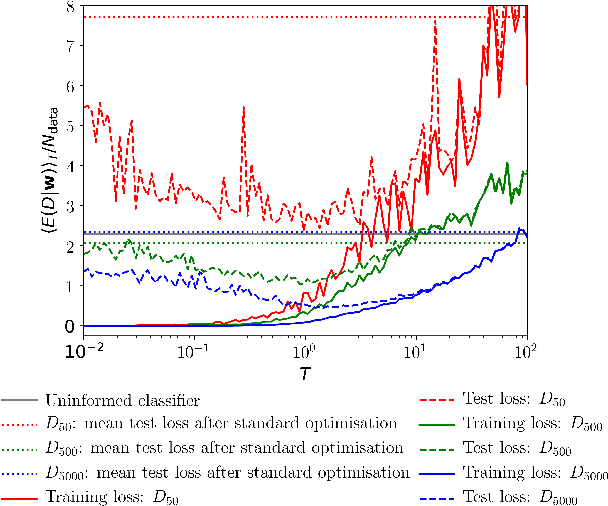
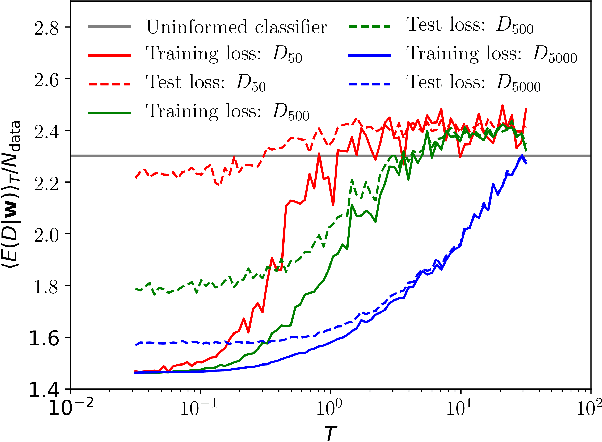
We recapitulate the Bayesian formulation of neural network based classifiers and show that, while sampling from the posterior does indeed lead to better generalisation than is obtained by standard optimisation of the cost function, even better performance can in general be achieved by sampling finite temperature ($T$) distributions derived from the posterior. Taking the example of two different deep (3 hidden layers) classifiers for MNIST data, we find quite different $T$ values to be appropriate in each case. In particular, for a typical neural network classifier a clear minimum of the test error is observed at $T>0$. This suggests an early stopping criterion for full batch simulated annealing: cool until the average validation error starts to increase, then revert to the parameters with the lowest validation error. As $T$ is increased classifiers transition from accurate classifiers to classifiers that have higher training error than assigning equal probability to each class. Efficient studies of these temperature-induced effects are enabled using a replica-exchange Hamiltonian Monte Carlo simulation technique. Finally, we show how thermodynamic integration can be used to perform model selection for deep neural networks. Similar to the Laplace approximation, this approach assumes that the posterior is dominated by a single mode. Crucially, however, no assumption is made about the shape of that mode and it is not required to precisely compute and invert the Hessian.