Statistically Near-Optimal Hypothesis Selection

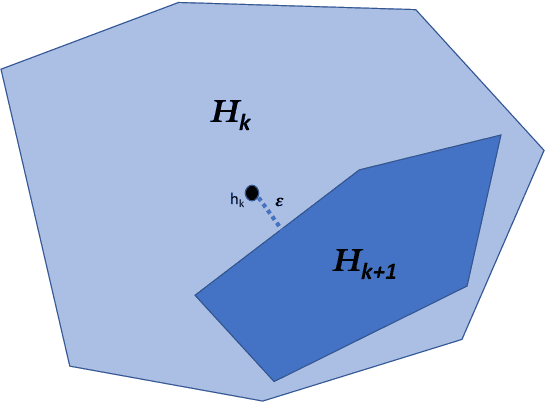
Hypothesis Selection is a fundamental distribution learning problem where given a comparator-class $Q=\{q_1,\ldots, q_n\}$ of distributions, and a sampling access to an unknown target distribution $p$, the goal is to output a distribution $q$ such that $\mathsf{TV}(p,q)$ is close to $opt$, where $opt = \min_i\{\mathsf{TV}(p,q_i)\}$ and $\mathsf{TV}(\cdot, \cdot)$ denotes the total-variation distance. Despite the fact that this problem has been studied since the 19th century, its complexity in terms of basic resources, such as number of samples and approximation guarantees, remains unsettled (this is discussed, e.g., in the charming book by Devroye and Lugosi `00). This is in stark contrast with other (younger) learning settings, such as PAC learning, for which these complexities are well understood. We derive an optimal $2$-approximation learning strategy for the Hypothesis Selection problem, outputting $q$ such that $\mathsf{TV}(p,q) \leq2 \cdot opt + \eps$, with a (nearly) optimal sample complexity of~$\tilde O(\log n/\epsilon^2)$. This is the first algorithm that simultaneously achieves the best approximation factor and sample complexity: previously, Bousquet, Kane, and Moran (COLT `19) gave a learner achieving the optimal $2$-approximation, but with an exponentially worse sample complexity of $\tilde O(\sqrt{n}/\epsilon^{2.5})$, and Yatracos~(Annals of Statistics `85) gave a learner with optimal sample complexity of $O(\log n /\epsilon^2)$ but with a sub-optimal approximation factor of $3$.

Non-parametric Binary regression in metric spaces with KL loss

We propose a non-parametric variant of binary regression, where the hypothesis is regularized to be a Lipschitz function taking a metric space to [0,1] and the loss is logarithmic. This setting presents novel computational and statistical challenges. On the computational front, we derive a novel efficient optimization algorithm based on interior point methods; an attractive feature is that it is parameter-free (i.e., does not require tuning an update step size). On the statistical front, the unbounded loss function presents a problem for classic generalization bounds, based on covering-number and Rademacher techniques. We get around this challenge via an adaptive truncation approach, and also present a lower bound indicating that the truncation is, in some sense, necessary.

Fast and Bayes-consistent nearest neighbors

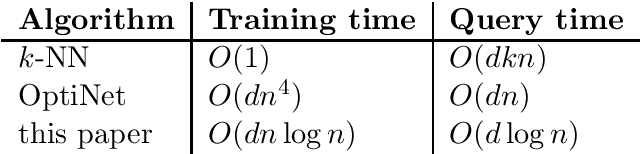
Research on nearest-neighbor methods tends to focus somewhat dichotomously either on the statistical or the computational aspects -- either on, say, Bayes consistency and rates of convergence or on techniques for speeding up the proximity search. This paper aims at bridging these realms: to reap the advantages of fast evaluation time while maintaining Bayes consistency, and further without sacrificing too much in the risk decay rate. We combine the locality-sensitive hashing (LSH) technique with a novel missing-mass argument to obtain a fast and Bayes-consistent classifier. Our algorithm's prediction runtime compares favorably against state of the art approximate NN methods, while maintaining Bayes-consistency and attaining rates comparable to minimax. On samples of size $n$ in $\R^d$, our pre-processing phase has runtime $O(d n \log n)$, while the evaluation phase has runtime $O(d\log n)$ per query point.