Scaling Analysis of Affinity Propagation
Paper and Code
Oct 09, 2009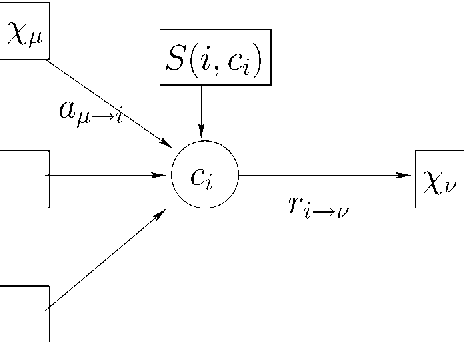

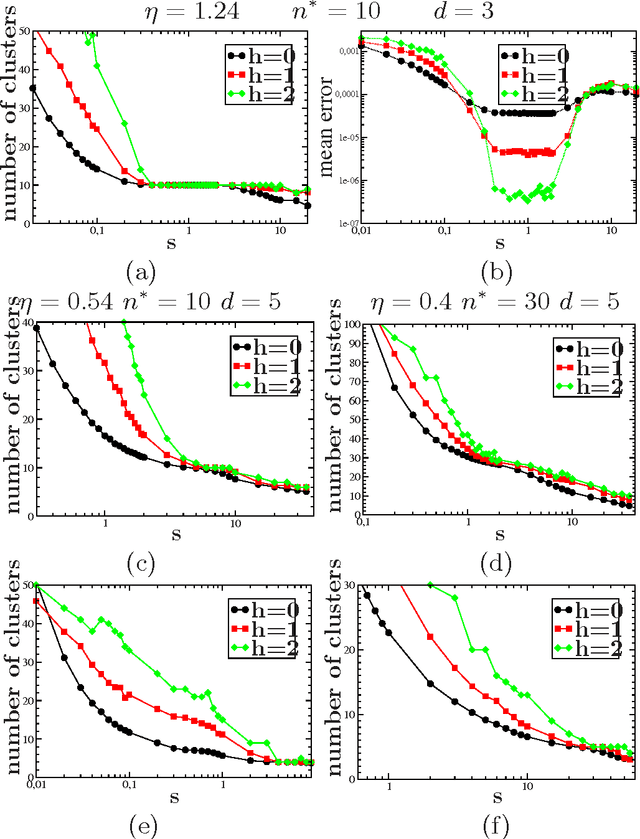
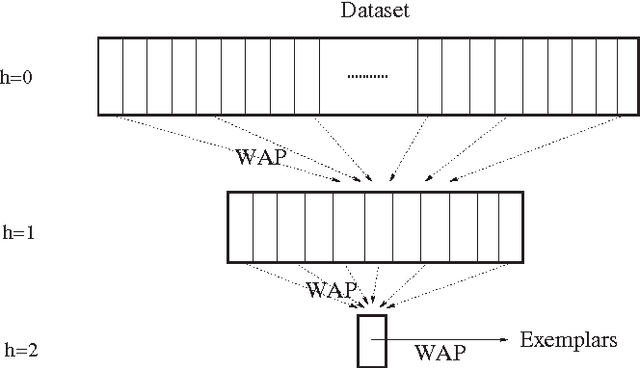
We analyze and exploit some scaling properties of the Affinity Propagation (AP) clustering algorithm proposed by Frey and Dueck (2007). First we observe that a divide and conquer strategy, used on a large data set hierarchically reduces the complexity ${\cal O}(N^2)$ to ${\cal O}(N^{(h+2)/(h+1)})$, for a data-set of size $N$ and a depth $h$ of the hierarchical strategy. For a data-set embedded in a $d$-dimensional space, we show that this is obtained without notably damaging the precision except in dimension $d=2$. In fact, for $d$ larger than 2 the relative loss in precision scales like $N^{(2-d)/(h+1)d}$. Finally, under some conditions we observe that there is a value $s^*$ of the penalty coefficient, a free parameter used to fix the number of clusters, which separates a fragmentation phase (for $s<s^*$) from a coalescent one (for $s>s^*$) of the underlying hidden cluster structure. At this precise point holds a self-similarity property which can be exploited by the hierarchical strategy to actually locate its position. From this observation, a strategy based on \AP can be defined to find out how many clusters are present in a given dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge