ANaGRAM: A Natural Gradient Relative to Adapted Model for efficient PINNs learning

In the recent years, Physics Informed Neural Networks (PINNs) have received strong interest as a method to solve PDE driven systems, in particular for data assimilation purpose. This method is still in its infancy, with many shortcomings and failures that remain not properly understood. In this paper we propose a natural gradient approach to PINNs which contributes to speed-up and improve the accuracy of the training. Based on an in depth analysis of the differential geometric structures of the problem, we come up with two distinct contributions: (i) a new natural gradient algorithm that scales as $\min(P^2S, S^2P)$, where $P$ is the number of parameters, and $S$ the batch size; (ii) a mathematically principled reformulation of the PINNs problem that allows the extension of natural gradient to it, with proved connections to Green's function theory.

Fast, accurate training and sampling of Restricted Boltzmann Machines

Thanks to their simple architecture, Restricted Boltzmann Machines (RBMs) are powerful tools for modeling complex systems and extracting interpretable insights from data. However, training RBMs, as other energy-based models, on highly structured data poses a major challenge, as effective training relies on mixing the Markov chain Monte Carlo simulations used to estimate the gradient. This process is often hindered by multiple second-order phase transitions and the associated critical slowdown. In this paper, we present an innovative method in which the principal directions of the dataset are integrated into a low-rank RBM through a convex optimization procedure. This approach enables efficient sampling of the equilibrium measure via a static Monte Carlo process. By starting the standard training process with a model that already accurately represents the main modes of the data, we bypass the initial phase transitions. Our results show that this strategy successfully trains RBMs to capture the full diversity of data in datasets where previous methods fail. Furthermore, we use the training trajectories to propose a new sampling method, {\em parallel trajectory tempering}, which allows us to sample the equilibrium measure of the trained model much faster than previous optimized MCMC approaches and a better estimation of the log-likelihood. We illustrate the success of the training method on several highly structured datasets.

Inferring effective couplings with Restricted Boltzmann Machines

Generative models offer a direct way to model complex data. Among them, energy-based models provide us with a neural network model that aims to accurately reproduce all statistical correlations observed in the data at the level of the Boltzmann weight of the model. However, one challenge is to understand the physical interpretation of such models. In this study, we propose a simple solution by implementing a direct mapping between the energy function of the Restricted Boltzmann Machine and an effective Ising spin Hamiltonian that includes high-order interactions between spins. This mapping includes interactions of all possible orders, going beyond the conventional pairwise interactions typically considered in the inverse Ising approach, and allowing the description of complex datasets. Earlier works attempted to achieve this goal, but the proposed mappings did not do properly treat the complexity of the problem or did not contain direct prescriptions for practical application. To validate our method, we performed several controlled numerical experiments where we trained the RBMs using equilibrium samples of predefined models containing local external fields, two-body and three-body interactions in various low-dimensional topologies. The results demonstrate the effectiveness of our proposed approach in learning the correct interaction network and pave the way for its application in modeling interesting datasets. We also evaluate the quality of the inferred model based on different training methods.

Learning a Restricted Boltzmann Machine using biased Monte Carlo sampling

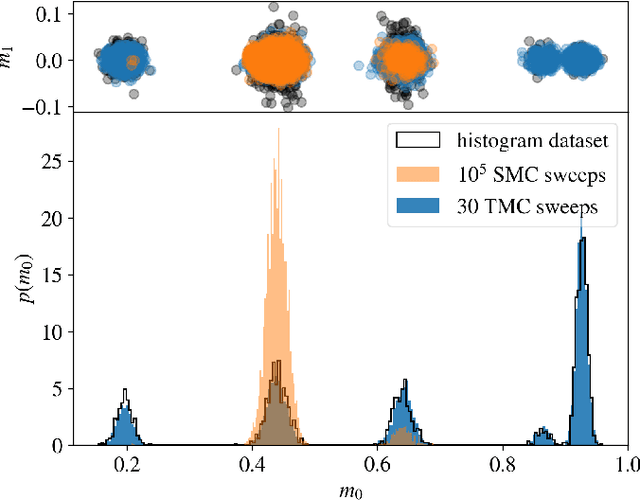
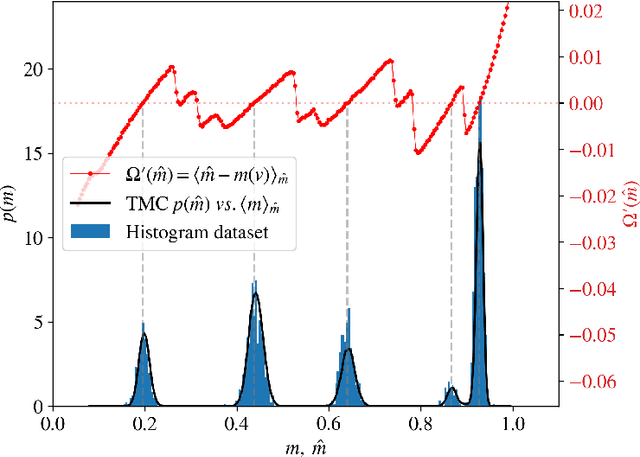
Restricted Boltzmann Machines are simple and powerful generative models capable of encoding any complex dataset. Despite all their advantages, in practice, trainings are often unstable, and it is hard to assess their quality because dynamics are hampered by extremely slow time-dependencies. This situation becomes critical when dealing with low-dimensional clustered datasets, where the time needed to sample ergodically the trained models becomes computationally prohibitive. In this work, we show that this divergence of Monte Carlo mixing times is related to a phase coexistence phenomenon, similar to that encountered in Physics in the vicinity of a first order phase transition. We show that sampling the equilibrium distribution via Markov Chain Monte Carlo can be dramatically accelerated using biased sampling techniques, in particular, the Tethered Monte Carlo method (TMC). This sampling technique solves efficiently the problem of evaluating the quality of a given trained model and the generation of new samples in reasonable times. In addition, we show that this sampling technique can be exploited to improve the computation of the log-likelihood gradient during the training too, which produces dramatic improvements when training RBMs with artificial clustered datasets. When dealing with real low-dimensional datasets, this new training procedure fits RBM models with significantly faster relaxational dynamics than those obtained with standard PCD recipes. We also show that TMC sampling can be used to recover free-energy profile of the RBM, which turns out to be extremely useful to compute the probability distribution of a given model and to improve the generation of new decorrelated samples on slow PCD trained models.

Equilibrium and non-Equilibrium regimes in the learning of Restricted Boltzmann Machines

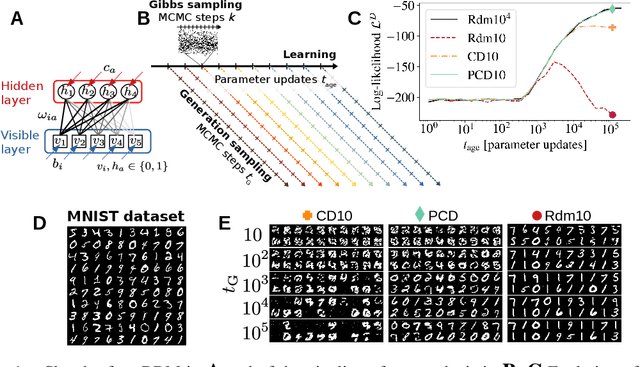
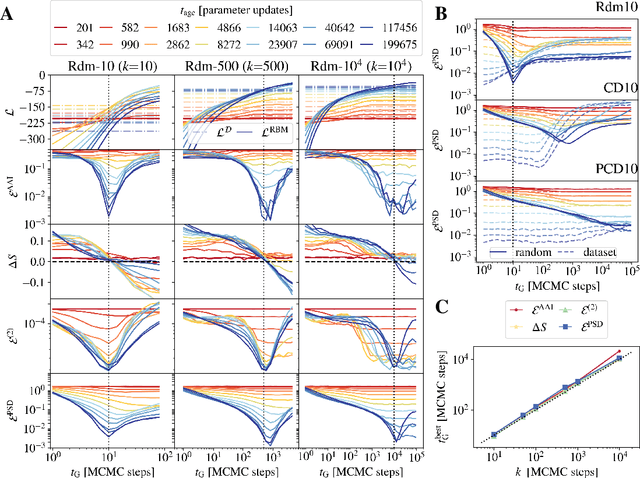
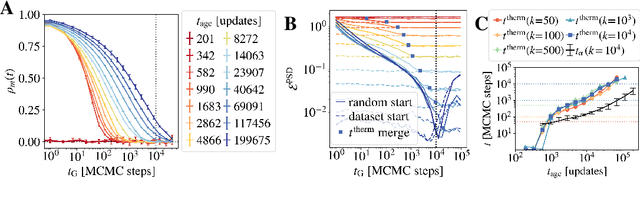
Training Restricted Boltzmann Machines (RBMs) has been challenging for a long time due to the difficulty of computing precisely the log-likelihood gradient. Over the past decades, many works have proposed more or less successful training recipes but without studying the crucial quantity of the problem: the mixing time i.e. the number of Monte Carlo iterations needed to sample new configurations from a model. In this work, we show that this mixing time plays a crucial role in the dynamics and stability of the trained model, and that RBMs operate in two well-defined regimes, namely equilibrium and out-of-equilibrium, depending on the interplay between this mixing time of the model and the number of steps, $k$, used to approximate the gradient. We further show empirically that this mixing time increases with the learning, which often implies a transition from one regime to another as soon as $k$ becomes smaller than this time. In particular, we show that using the popular $k$ (persistent) contrastive divergence approaches, with $k$ small, the dynamics of the learned model are extremely slow and often dominated by strong out-of-equilibrium effects. On the contrary, RBMs trained in equilibrium display faster dynamics, and a smooth convergence to dataset-like configurations during the sampling. Finally we discuss how to exploit in practice both regimes depending on the task one aims to fulfill: (i) short $k$s can be used to generate convincing samples in short times, (ii) large $k$ (or increasingly large) must be used to learn the correct equilibrium distribution of the RBM.

Restricted Boltzmann Machine, recent advances and mean-field theory

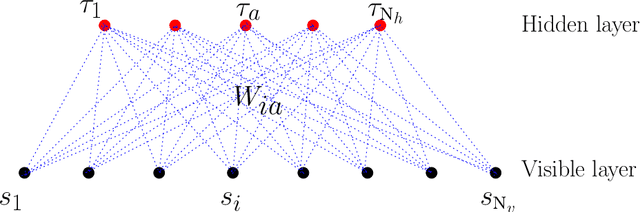
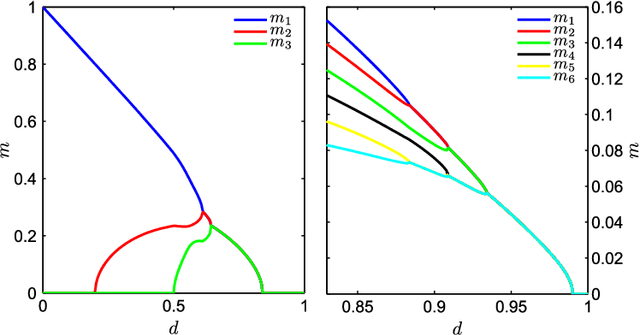
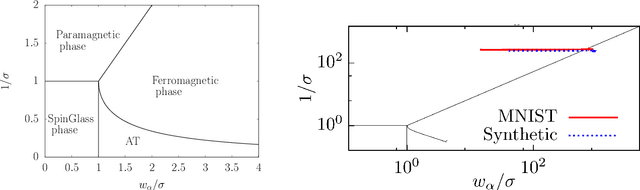
This review deals with Restricted Boltzmann Machine (RBM) under the light of statistical physics. The RBM is a classical family of Machine learning (ML) models which played a central role in the development of deep learning. Viewing it as a Spin Glass model and exhibiting various links with other models of statistical physics, we gather recent results dealing with mean-field theory in this context. First the functioning of the RBM can be analyzed via the phase diagrams obtained for various statistical ensembles of RBM leading in particular to identify a {\it compositional phase} where a small number of features or modes are combined to form complex patterns. Then we discuss recent works either able to devise mean-field based learning algorithms; either able to reproduce generic aspects of the learning process from some {\it ensemble dynamics equations} or/and from linear stability arguments.

Robust Multi-Output Learning with Highly Incomplete Data via Restricted Boltzmann Machines

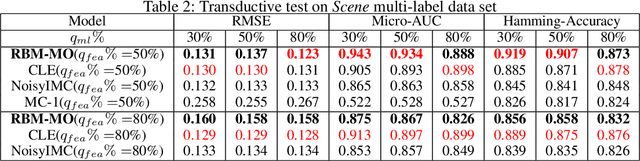
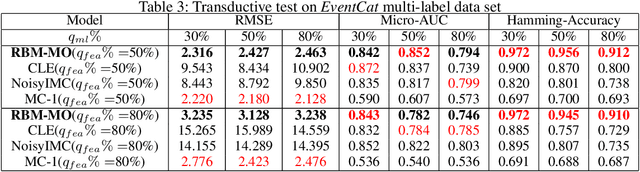
In a standard multi-output classification scenario, both features and labels of training data are partially observed. This challenging issue is widely witnessed due to sensor or database failures, crowd-sourcing and noisy communication channels in industrial data analytic services. Classic methods for handling multi-output classification with incomplete supervision information usually decompose the problem into an imputation stage that reconstructs the missing training information, and a learning stage that builds a classifier based on the imputed training set. These methods fail to fully leverage the dependencies between features and labels. In order to take full advantage of these dependencies we consider a purely probabilistic setting in which the features imputation and multi-label classification problems are jointly solved. Indeed, we show that a simple Restricted Boltzmann Machine can be trained with an adapted algorithm based on mean-field equations to efficiently solve problems of inductive and transductive learning in which both features and labels are missing at random. The effectiveness of the approach is demonstrated empirically on various datasets, with particular focus on a real-world Internet-of-Things security dataset.

Gaussian-Spherical Restricted Boltzmann Machines

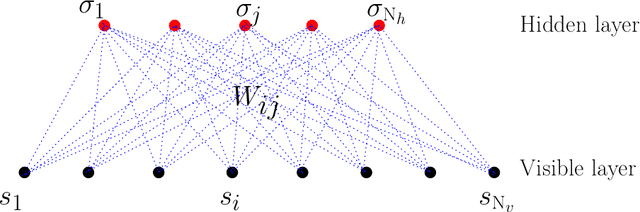
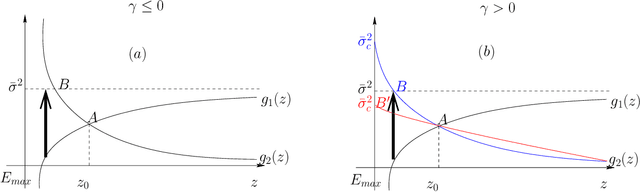
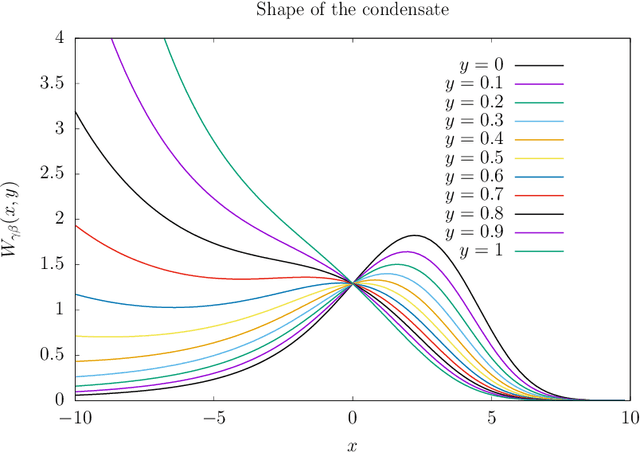
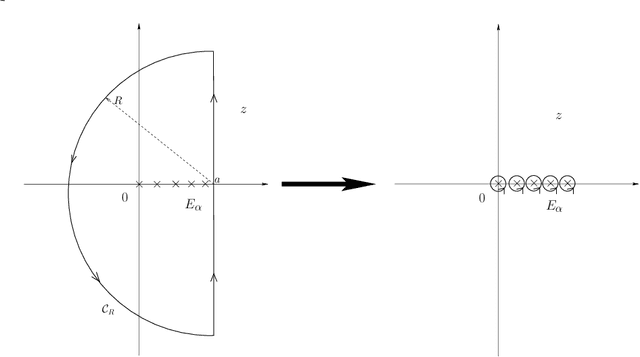
We consider a special type of Restricted Boltzmann machine (RBM), namely a Gaussian-spherical RBM where the visible units have Gaussian priors while the vector of hidden variables is constrained to stay on an ${\mathbbm L}_2$ sphere. The spherical constraint having the advantage to admit exact asymptotic treatments, various scaling regimes are explicitly identified based solely on the spectral properties of the coupling matrix (also called weight matrix of the RBM). Incidentally these happen to be formally related to similar scaling behaviours obtained in a different context dealing with spatial condensation of zero range processes. More specifically, when the spectrum of the coupling matrix is doubly degenerated an exact treatment can be proposed to deal with finite size effects. Interestingly the known parallel between the ferromagnetic transition of the spherical model and the Bose-Einstein condensation can be made explicit in that case. More importantly this gives us the ability to extract all needed response functions with arbitrary precision for the training algorithm of the RBM. This allows us then to numerically integrate the dynamics of the spectrum of the weight matrix during learning in a precise way. This dynamics reveals in particular a sequential emergence of modes from the Marchenko-Pastur bulk of singular vectors of the coupling matrix.

Thermodynamics of Restricted Boltzmann Machines and related learning dynamics

We investigate the thermodynamic properties of a Restricted Boltzmann Machine (RBM), a simple energy-based generative model used in the context of unsupervised learning. Assuming the information content of this model to be mainly reflected by the spectral properties of its weight matrix $W$, we try to make a realistic analysis by averaging over an appropriate statistical ensemble of RBMs. First, a phase diagram is derived. Otherwise similar to that of the Sherrington- Kirkpatrick (SK) model with ferromagnetic couplings, the RBM's phase diagram presents a ferromagnetic phase which may or may not be of compositional type depending on the kurtosis of the distribution of the components of the singular vectors of $W$. Subsequently, the learning dynamics of the RBM is studied in the thermodynamic limit. A "typical" learning trajectory is shown to solve an effective dynamical equation, based on the aforementioned ensemble average and explicitly involving order parameters obtained from the thermodynamic analysis. In particular, this let us show how the evolution of the dominant singular values of $W$, and thus of the unstable modes, is driven by the input data. At the beginning of the training, in which the RBM is found to operate in the linear regime, the unstable modes reflect the dominant covariance modes of the data. In the non-linear regime, instead, the selected modes interact and eventually impose a matching of the order parameters to their empirical counterparts estimated from the data. Finally, we illustrate our considerations by performing experiments on both artificial and real data, showing in particular how the RBM operates in the ferromagnetic compositional phase.

Spectral Dynamics of Learning Restricted Boltzmann Machines

The Restricted Boltzmann Machine (RBM), an important tool used in machine learning in particular for unsupervized learning tasks, is investigated from the perspective of its spectral properties. Starting from empirical observations, we propose a generic statistical ensemble for the weight matrix of the RBM and characterize its mean evolution. This let us show how in the linear regime, in which the RBM is found to operate at the beginning of the training, the statistical properties of the data drive the selection of the unstable modes of the weight matrix. A set of equations characterizing the non-linear regime is then derived, unveiling in some way how the selected modes interact in later stages of the learning procedure and defining a deterministic learning curve for the RBM.