Relative gradient optimization of the Jacobian term in unsupervised deep learning

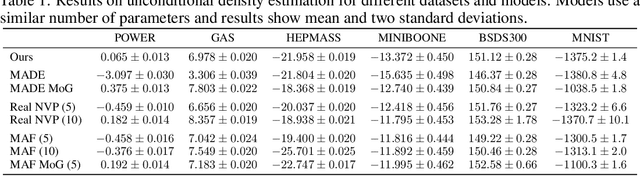
Learning expressive probabilistic models correctly describing the data is a ubiquitous problem in machine learning. A popular approach for solving it is mapping the observations into a representation space with a simple joint distribution, which can typically be written as a product of its marginals -- thus drawing a connection with the field of nonlinear independent component analysis. Deep density models have been widely used for this task, but their likelihood-based training requires estimating the log-determinant of the Jacobian and is computationally expensive, thus imposing a trade-off between computation and expressive power. In this work, we propose a new approach for exact likelihood-based training of such neural networks. Based on relative gradients, we exploit the matrix structure of neural network parameters to compute updates efficiently even in high-dimensional spaces; the computational cost of the training is quadratic in the input size, in contrast with the cubic scaling of the naive approaches. This allows fast training with objective functions involving the log-determinant of the Jacobian without imposing constraints on its structure, in stark contrast to normalizing flows. An implementation of our method can be found at https://github.com/fissoreg/relative-gradient-jacobian

Robust Multi-Output Learning with Highly Incomplete Data via Restricted Boltzmann Machines

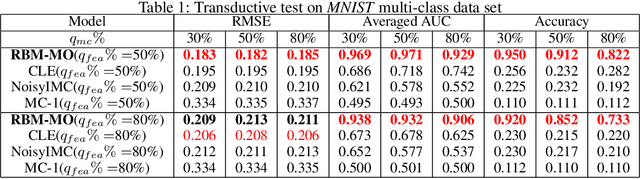
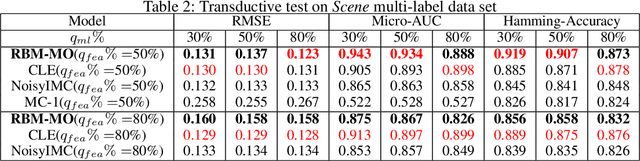
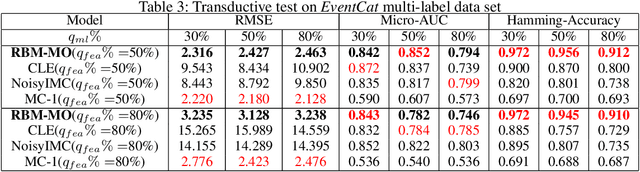
In a standard multi-output classification scenario, both features and labels of training data are partially observed. This challenging issue is widely witnessed due to sensor or database failures, crowd-sourcing and noisy communication channels in industrial data analytic services. Classic methods for handling multi-output classification with incomplete supervision information usually decompose the problem into an imputation stage that reconstructs the missing training information, and a learning stage that builds a classifier based on the imputed training set. These methods fail to fully leverage the dependencies between features and labels. In order to take full advantage of these dependencies we consider a purely probabilistic setting in which the features imputation and multi-label classification problems are jointly solved. Indeed, we show that a simple Restricted Boltzmann Machine can be trained with an adapted algorithm based on mean-field equations to efficiently solve problems of inductive and transductive learning in which both features and labels are missing at random. The effectiveness of the approach is demonstrated empirically on various datasets, with particular focus on a real-world Internet-of-Things security dataset.

Thermodynamics of Restricted Boltzmann Machines and related learning dynamics

We investigate the thermodynamic properties of a Restricted Boltzmann Machine (RBM), a simple energy-based generative model used in the context of unsupervised learning. Assuming the information content of this model to be mainly reflected by the spectral properties of its weight matrix $W$, we try to make a realistic analysis by averaging over an appropriate statistical ensemble of RBMs. First, a phase diagram is derived. Otherwise similar to that of the Sherrington- Kirkpatrick (SK) model with ferromagnetic couplings, the RBM's phase diagram presents a ferromagnetic phase which may or may not be of compositional type depending on the kurtosis of the distribution of the components of the singular vectors of $W$. Subsequently, the learning dynamics of the RBM is studied in the thermodynamic limit. A "typical" learning trajectory is shown to solve an effective dynamical equation, based on the aforementioned ensemble average and explicitly involving order parameters obtained from the thermodynamic analysis. In particular, this let us show how the evolution of the dominant singular values of $W$, and thus of the unstable modes, is driven by the input data. At the beginning of the training, in which the RBM is found to operate in the linear regime, the unstable modes reflect the dominant covariance modes of the data. In the non-linear regime, instead, the selected modes interact and eventually impose a matching of the order parameters to their empirical counterparts estimated from the data. Finally, we illustrate our considerations by performing experiments on both artificial and real data, showing in particular how the RBM operates in the ferromagnetic compositional phase.

Spectral Dynamics of Learning Restricted Boltzmann Machines

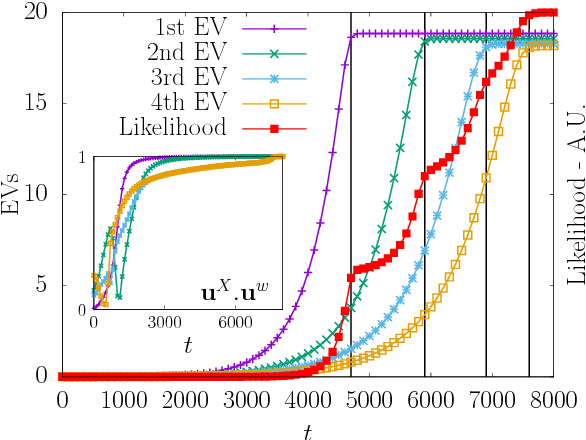
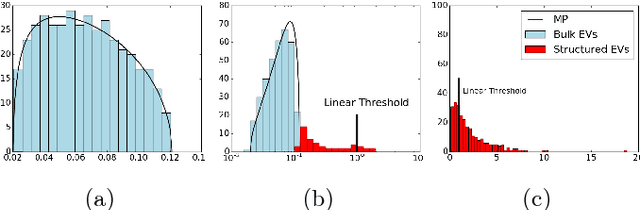
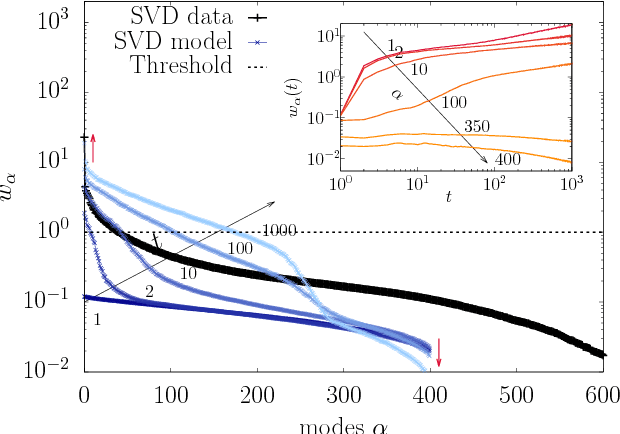
The Restricted Boltzmann Machine (RBM), an important tool used in machine learning in particular for unsupervized learning tasks, is investigated from the perspective of its spectral properties. Starting from empirical observations, we propose a generic statistical ensemble for the weight matrix of the RBM and characterize its mean evolution. This let us show how in the linear regime, in which the RBM is found to operate at the beginning of the training, the statistical properties of the data drive the selection of the unstable modes of the weight matrix. A set of equations characterizing the non-linear regime is then derived, unveiling in some way how the selected modes interact in later stages of the learning procedure and defining a deterministic learning curve for the RBM.