Fast, accurate training and sampling of Restricted Boltzmann Machines

Thanks to their simple architecture, Restricted Boltzmann Machines (RBMs) are powerful tools for modeling complex systems and extracting interpretable insights from data. However, training RBMs, as other energy-based models, on highly structured data poses a major challenge, as effective training relies on mixing the Markov chain Monte Carlo simulations used to estimate the gradient. This process is often hindered by multiple second-order phase transitions and the associated critical slowdown. In this paper, we present an innovative method in which the principal directions of the dataset are integrated into a low-rank RBM through a convex optimization procedure. This approach enables efficient sampling of the equilibrium measure via a static Monte Carlo process. By starting the standard training process with a model that already accurately represents the main modes of the data, we bypass the initial phase transitions. Our results show that this strategy successfully trains RBMs to capture the full diversity of data in datasets where previous methods fail. Furthermore, we use the training trajectories to propose a new sampling method, {\em parallel trajectory tempering}, which allows us to sample the equilibrium measure of the trained model much faster than previous optimized MCMC approaches and a better estimation of the log-likelihood. We illustrate the success of the training method on several highly structured datasets.

Learning a Restricted Boltzmann Machine using biased Monte Carlo sampling

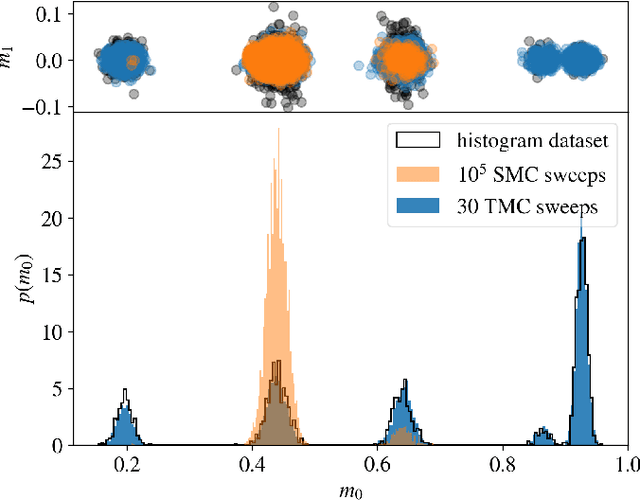
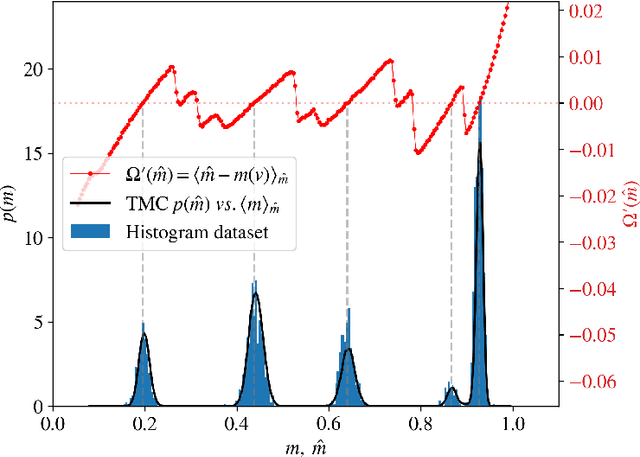
Restricted Boltzmann Machines are simple and powerful generative models capable of encoding any complex dataset. Despite all their advantages, in practice, trainings are often unstable, and it is hard to assess their quality because dynamics are hampered by extremely slow time-dependencies. This situation becomes critical when dealing with low-dimensional clustered datasets, where the time needed to sample ergodically the trained models becomes computationally prohibitive. In this work, we show that this divergence of Monte Carlo mixing times is related to a phase coexistence phenomenon, similar to that encountered in Physics in the vicinity of a first order phase transition. We show that sampling the equilibrium distribution via Markov Chain Monte Carlo can be dramatically accelerated using biased sampling techniques, in particular, the Tethered Monte Carlo method (TMC). This sampling technique solves efficiently the problem of evaluating the quality of a given trained model and the generation of new samples in reasonable times. In addition, we show that this sampling technique can be exploited to improve the computation of the log-likelihood gradient during the training too, which produces dramatic improvements when training RBMs with artificial clustered datasets. When dealing with real low-dimensional datasets, this new training procedure fits RBM models with significantly faster relaxational dynamics than those obtained with standard PCD recipes. We also show that TMC sampling can be used to recover free-energy profile of the RBM, which turns out to be extremely useful to compute the probability distribution of a given model and to improve the generation of new decorrelated samples on slow PCD trained models.