DCDILP: a distributed learning method for large-scale causal structure learning

This paper presents a novel approach to causal discovery through a divide-and-conquer framework. By decomposing the problem into smaller subproblems defined on Markov blankets, the proposed DCDILP method first explores in parallel the local causal graphs of these subproblems. However, this local discovery phase encounters systematic challenges due to the presence of hidden confounders (variables within each Markov blanket may be influenced by external variables). Moreover, aggregating these local causal graphs in a consistent global graph defines a large size combinatorial optimization problem. DCDILP addresses these challenges by: i) restricting the local subgraphs to causal links only related with the central variable of the Markov blanket; ii) formulating the reconciliation of local causal graphs as an integer linear programming method. The merits of the approach, in both terms of causal discovery accuracy and scalability in the size of the problem, are showcased by experiments and comparisons with the state of the art.

A Latent Diffusion Model for Protein Structure Generation

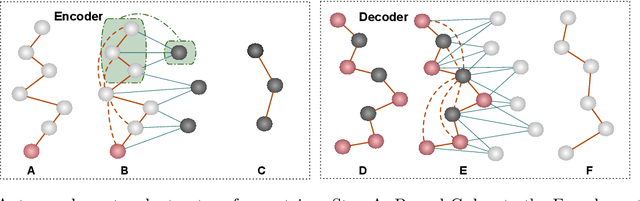
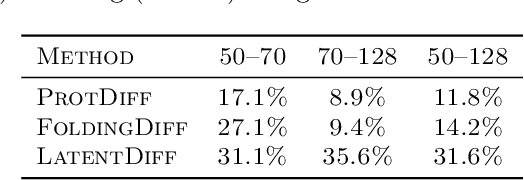
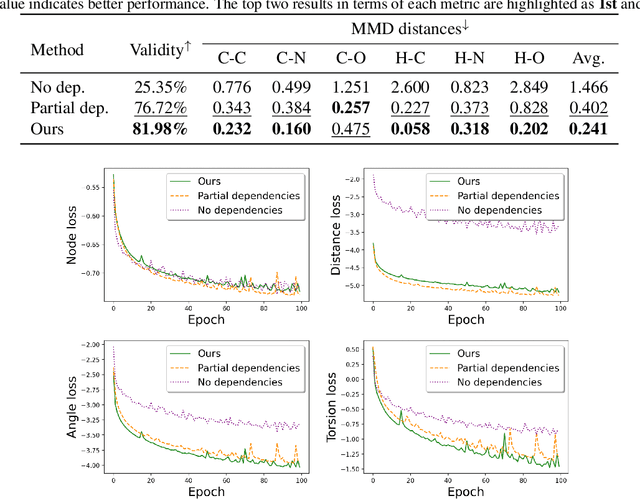
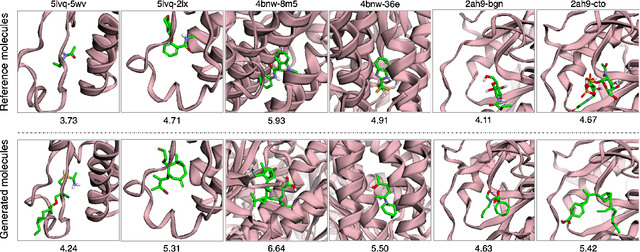
Proteins are complex biomolecules that perform a variety of crucial functions within living organisms. Designing and generating novel proteins can pave the way for many future synthetic biology applications, including drug discovery. However, it remains a challenging computational task due to the large modeling space of protein structures. In this study, we propose a latent diffusion model that can reduce the complexity of protein modeling while flexibly capturing the distribution of natural protein structures in a condensed latent space. Specifically, we propose an equivariant protein autoencoder that embeds proteins into a latent space and then uses an equivariant diffusion model to learn the distribution of the latent protein representations. Experimental results demonstrate that our method can effectively generate novel protein backbone structures with high designability and efficiency.

High-Dimensional Causal Discovery: Learning from Inverse Covariance via Independence-based Decomposition

Inferring causal relationships from observational data is a fundamental yet highly complex problem when the number of variables is large. Recent advances have made much progress in learning causal structure models (SEMs) but still face challenges in scalability. This paper aims to efficiently discover causal DAGs from high-dimensional data. We investigate a way of recovering causal DAGs from inverse covariance estimators of the observational data. The proposed algorithm, called ICID (inverse covariance estimation and {\it independence-based} decomposition), searches for a decomposition of the inverse covariance matrix that preserves its nonzero patterns. This algorithm benefits from properties of positive definite matrices supported on {\it chordal} graphs and the preservation of nonzero patterns in their Cholesky decomposition; we find exact mirroring between the support-preserving property and the independence-preserving property of our decomposition method, which explains its effectiveness in identifying causal structures from the data distribution. We show that the proposed algorithm recovers causal DAGs with a complexity of $O(d^2)$ in the context of sparse SEMs. The advantageously low complexity is reflected by good scalability of our algorithm in thorough experiments and comparisons with state-of-the-art algorithms.

Generating 3D Molecules for Target Protein Binding

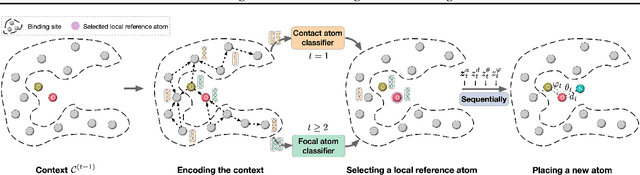
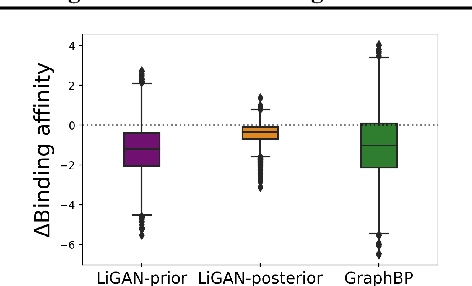
A fundamental problem in drug discovery is to design molecules that bind to specific proteins. To tackle this problem using machine learning methods, here we propose a novel and effective framework, known as GraphBP, to generate 3D molecules that bind to given proteins by placing atoms of specific types and locations to the given binding site one by one. In particular, at each step, we first employ a 3D graph neural network to obtain geometry-aware and chemically informative representations from the intermediate contextual information. Such context includes the given binding site and atoms placed in the previous steps. Second, to preserve the desirable equivariance property, we select a local reference atom according to the designed auxiliary classifiers and then construct a local spherical coordinate system. Finally, to place a new atom, we generate its atom type and relative location w.r.t. the constructed local coordinate system via a flow model. We also consider generating the variables of interest sequentially to capture the underlying dependencies among them. Experiments demonstrate that our GraphBP is effective to generate 3D molecules with binding ability to target protein binding sites. Our implementation is available at https://github.com/divelab/GraphBP.

Inter-domain Multi-relational Link Prediction

Multi-relational graph is a ubiquitous and important data structure, allowing flexible representation of multiple types of interactions and relations between entities. Similar to other graph-structured data, link prediction is one of the most important tasks on multi-relational graphs and is often used for knowledge completion. When related graphs coexist, it is of great benefit to build a larger graph via integrating the smaller ones. The integration requires predicting hidden relational connections between entities belonged to different graphs (inter-domain link prediction). However, this poses a real challenge to existing methods that are exclusively designed for link prediction between entities of the same graph only (intra-domain link prediction). In this study, we propose a new approach to tackle the inter-domain link prediction problem by softly aligning the entity distributions between different domains with optimal transport and maximum mean discrepancy regularizers. Experiments on real-world datasets show that optimal transport regularizer is beneficial and considerably improves the performance of baseline methods.

Crowdsourcing Evaluation of Saliency-based XAI Methods

Understanding the reasons behind the predictions made by deep neural networks is critical for gaining human trust in many important applications, which is reflected in the increasing demand for explainability in AI (XAI) in recent years. Saliency-based feature attribution methods, which highlight important parts of images that contribute to decisions by classifiers, are often used as XAI methods, especially in the field of computer vision. In order to compare various saliency-based XAI methods quantitatively, several approaches for automated evaluation schemes have been proposed; however, there is no guarantee that such automated evaluation metrics correctly evaluate explainability, and a high rating by an automated evaluation scheme does not necessarily mean a high explainability for humans. In this study, instead of the automated evaluation, we propose a new human-based evaluation scheme using crowdsourcing to evaluate XAI methods. Our method is inspired by a human computation game, "Peek-a-boom", and can efficiently compare different XAI methods by exploiting the power of crowds. We evaluate the saliency maps of various XAI methods on two datasets with automated and crowd-based evaluation schemes. Our experiments show that the result of our crowd-based evaluation scheme is different from those of automated evaluation schemes. In addition, we regard the crowd-based evaluation results as ground truths and provide a quantitative performance measure to compare different automated evaluation schemes. We also discuss the impact of crowd workers on the results and show that the varying ability of crowd workers does not significantly impact the results.

Bermuda Triangles: GNNs Fail to Detect Simple Topological Structures

Most graph neural network architectures work by message-passing node vector embeddings over the adjacency matrix, and it is assumed that they capture graph topology by doing that. We design two synthetic tasks, focusing purely on topological problems -- triangle detection and clique distance -- on which graph neural networks perform surprisingly badly, failing to detect those "bermuda" triangles. Datasets and their generation scripts are publicly available on github.com/FujitsuLaboratories/bermudatriangles and dataset.labs.fujitsu.com.

Linear Tensor Projection Revealing Nonlinearity

Dimensionality reduction is an effective method for learning high-dimensional data, which can provide better understanding of decision boundaries in human-readable low-dimensional subspace. Linear methods, such as principal component analysis and linear discriminant analysis, make it possible to capture the correlation between many variables; however, there is no guarantee that the correlations that are important in predicting data can be captured. Moreover, if the decision boundary has strong nonlinearity, the guarantee becomes increasingly difficult. This problem is exacerbated when the data are matrices or tensors that represent relationships between variables. We propose a learning method that searches for a subspace that maximizes the prediction accuracy while retaining as much of the original data information as possible, even if the prediction model in the subspace has strong nonlinearity. This makes it easier to interpret the mechanism of the group of variables behind the prediction problem that the user wants to know. We show the effectiveness of our method by applying it to various types of data including matrices and tensors.