DCDILP: a distributed learning method for large-scale causal structure learning

This paper presents a novel approach to causal discovery through a divide-and-conquer framework. By decomposing the problem into smaller subproblems defined on Markov blankets, the proposed DCDILP method first explores in parallel the local causal graphs of these subproblems. However, this local discovery phase encounters systematic challenges due to the presence of hidden confounders (variables within each Markov blanket may be influenced by external variables). Moreover, aggregating these local causal graphs in a consistent global graph defines a large size combinatorial optimization problem. DCDILP addresses these challenges by: i) restricting the local subgraphs to causal links only related with the central variable of the Markov blanket; ii) formulating the reconciliation of local causal graphs as an integer linear programming method. The merits of the approach, in both terms of causal discovery accuracy and scalability in the size of the problem, are showcased by experiments and comparisons with the state of the art.

High-Dimensional Causal Discovery: Learning from Inverse Covariance via Independence-based Decomposition

Inferring causal relationships from observational data is a fundamental yet highly complex problem when the number of variables is large. Recent advances have made much progress in learning causal structure models (SEMs) but still face challenges in scalability. This paper aims to efficiently discover causal DAGs from high-dimensional data. We investigate a way of recovering causal DAGs from inverse covariance estimators of the observational data. The proposed algorithm, called ICID (inverse covariance estimation and {\it independence-based} decomposition), searches for a decomposition of the inverse covariance matrix that preserves its nonzero patterns. This algorithm benefits from properties of positive definite matrices supported on {\it chordal} graphs and the preservation of nonzero patterns in their Cholesky decomposition; we find exact mirroring between the support-preserving property and the independence-preserving property of our decomposition method, which explains its effectiveness in identifying causal structures from the data distribution. We show that the proposed algorithm recovers causal DAGs with a complexity of $O(d^2)$ in the context of sparse SEMs. The advantageously low complexity is reflected by good scalability of our algorithm in thorough experiments and comparisons with state-of-the-art algorithms.

Ordered Counterfactual Explanation by Mixed-Integer Linear Optimization

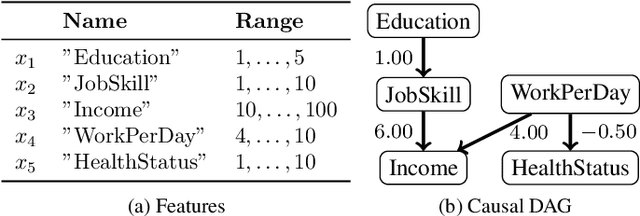
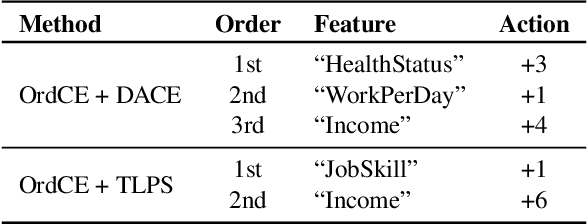
Post-hoc explanation methods for machine learning models have been widely used to support decision-making. One of the popular methods is Counterfactual Explanation (CE), which provides a user with a perturbation vector of features that alters the prediction result. Given a perturbation vector, a user can interpret it as an "action" for obtaining one's desired decision result. In practice, however, showing only a perturbation vector is often insufficient for users to execute the action. The reason is that if there is an asymmetric interaction among features, such as causality, the total cost of the action is expected to depend on the order of changing features. Therefore, practical CE methods are required to provide an appropriate order of changing features in addition to a perturbation vector. For this purpose, we propose a new framework called Ordered Counterfactual Explanation (OrdCE). We introduce a new objective function that evaluates a pair of an action and an order based on feature interaction. To extract an optimal pair, we propose a mixed-integer linear optimization approach with our objective function. Numerical experiments on real datasets demonstrated the effectiveness of our OrdCE in comparison with unordered CE methods.