Learning Decision Trees and Forests with Algorithmic Recourse

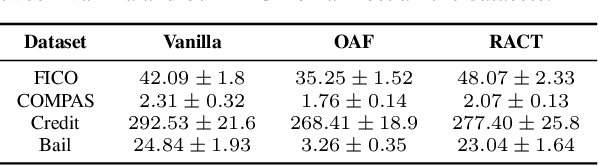
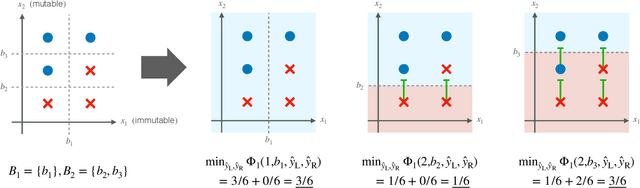
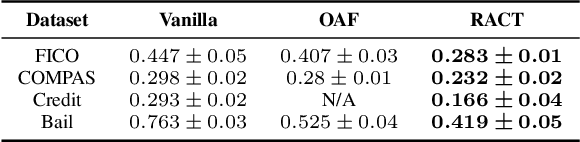
This paper proposes a new algorithm for learning accurate tree-based models while ensuring the existence of recourse actions. Algorithmic Recourse (AR) aims to provide a recourse action for altering the undesired prediction result given by a model. Typical AR methods provide a reasonable action by solving an optimization task of minimizing the required effort among executable actions. In practice, however, such actions do not always exist for models optimized only for predictive performance. To alleviate this issue, we formulate the task of learning an accurate classification tree under the constraint of ensuring the existence of reasonable actions for as many instances as possible. Then, we propose an efficient top-down greedy algorithm by leveraging the adversarial training techniques. We also show that our proposed algorithm can be applied to the random forest, which is known as a popular framework for learning tree ensembles. Experimental results demonstrated that our method successfully provided reasonable actions to more instances than the baselines without significantly degrading accuracy and computational efficiency.

Learning Locally Interpretable Rule Ensemble

This paper proposes a new framework for learning a rule ensemble model that is both accurate and interpretable. A rule ensemble is an interpretable model based on the linear combination of weighted rules. In practice, we often face the trade-off between the accuracy and interpretability of rule ensembles. That is, a rule ensemble needs to include a sufficiently large number of weighted rules to maintain its accuracy, which harms its interpretability for human users. To avoid this trade-off and learn an interpretable rule ensemble without degrading accuracy, we introduce a new concept of interpretability, named local interpretability, which is evaluated by the total number of rules necessary to express individual predictions made by the model, rather than to express the model itself. Then, we propose a regularizer that promotes local interpretability and develop an efficient algorithm for learning a rule ensemble with the proposed regularizer by coordinate descent with local search. Experimental results demonstrated that our method learns rule ensembles that can explain individual predictions with fewer rules than the existing methods, including RuleFit, while maintaining comparable accuracy.

Counterfactual Explanation with Missing Values

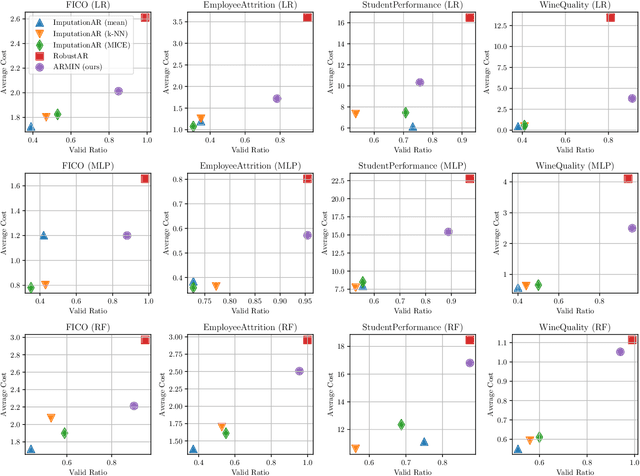
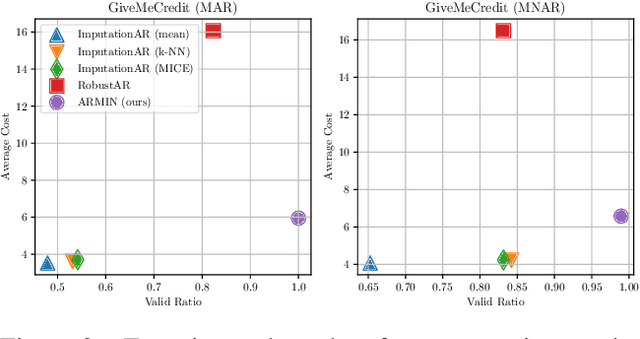
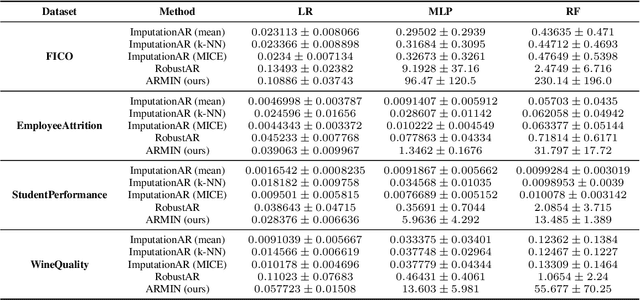
Counterfactual Explanation (CE) is a post-hoc explanation method that provides a perturbation for altering the prediction result of a classifier. Users can interpret the perturbation as an "action" to obtain their desired decision results. Existing CE methods require complete information on the features of an input instance. However, we often encounter missing values in a given instance, and the previous methods do not work in such a practical situation. In this paper, we first empirically and theoretically show the risk that missing value imputation methods affect the validity of an action, as well as the features that the action suggests changing. Then, we propose a new framework of CE, named Counterfactual Explanation by Pairs of Imputation and Action (CEPIA), that enables users to obtain valid actions even with missing values and clarifies how actions are affected by imputation of the missing values. Specifically, our CEPIA provides a representative set of pairs of an imputation candidate for a given incomplete instance and its optimal action. We formulate the problem of finding such a set as a submodular maximization problem, which can be solved by a simple greedy algorithm with an approximation guarantee. Experimental results demonstrated the efficacy of our CEPIA in comparison with the baselines in the presence of missing values.

Computing the Collection of Good Models for Rule Lists

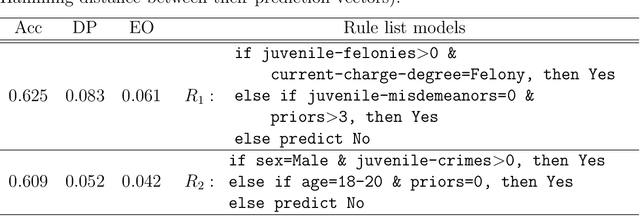
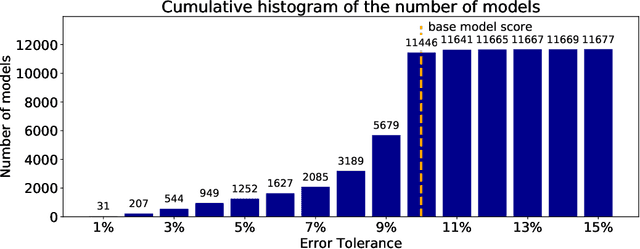
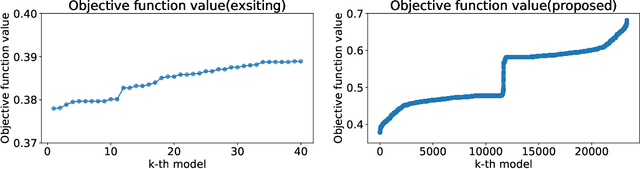
Since the seminal paper by Breiman in 2001, who pointed out a potential harm of prediction multiplicities from the view of explainable AI, global analysis of a collection of all good models, also known as a `Rashomon set,' has been attracted much attention for the last years. Since finding such a set of good models is a hard computational problem, there have been only a few algorithms for the problem so far, most of which are either approximate or incomplete. To overcome this difficulty, we study efficient enumeration of all good models for a subclass of interpretable models, called rule lists. Based on a state-of-the-art optimal rule list learner, CORELS, proposed by Angelino et al. in 2017, we present an efficient enumeration algorithm CorelsEnum for exactly computing a set of all good models using polynomial space in input size, given a dataset and a error tolerance from an optimal model. By experiments with the COMPAS dataset on recidivism prediction, our algorithm CorelsEnum successfully enumerated all of several tens of thousands of good rule lists of length at most $\ell = 3$ in around 1,000 seconds, while a state-of-the-art top-$K$ rule list learner based on Lawler's method combined with CORELS, proposed by Hara and Ishihata in 2018, found only 40 models until the timeout of 6,000 seconds. For global analysis, we conducted experiments for characterizing the Rashomon set, and observed large diversity of models in predictive multiplicity and fairness of models.

Ordered Counterfactual Explanation by Mixed-Integer Linear Optimization

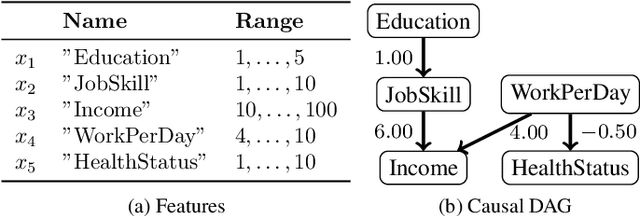
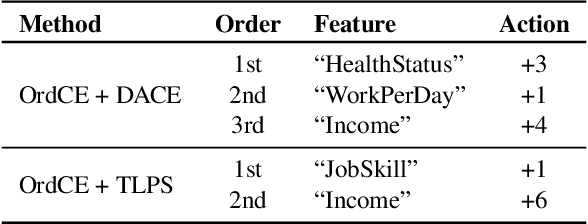
Post-hoc explanation methods for machine learning models have been widely used to support decision-making. One of the popular methods is Counterfactual Explanation (CE), which provides a user with a perturbation vector of features that alters the prediction result. Given a perturbation vector, a user can interpret it as an "action" for obtaining one's desired decision result. In practice, however, showing only a perturbation vector is often insufficient for users to execute the action. The reason is that if there is an asymmetric interaction among features, such as causality, the total cost of the action is expected to depend on the order of changing features. Therefore, practical CE methods are required to provide an appropriate order of changing features in addition to a perturbation vector. For this purpose, we propose a new framework called Ordered Counterfactual Explanation (OrdCE). We introduce a new objective function that evaluates a pair of an action and an order based on feature interaction. To extract an optimal pair, we propose a mixed-integer linear optimization approach with our objective function. Numerical experiments on real datasets demonstrated the effectiveness of our OrdCE in comparison with unordered CE methods.

Enumeration of Distinct Support Vectors for Interactive Decision Making

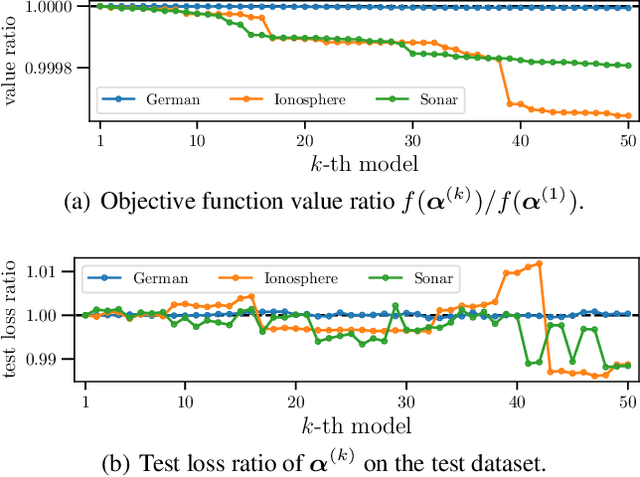
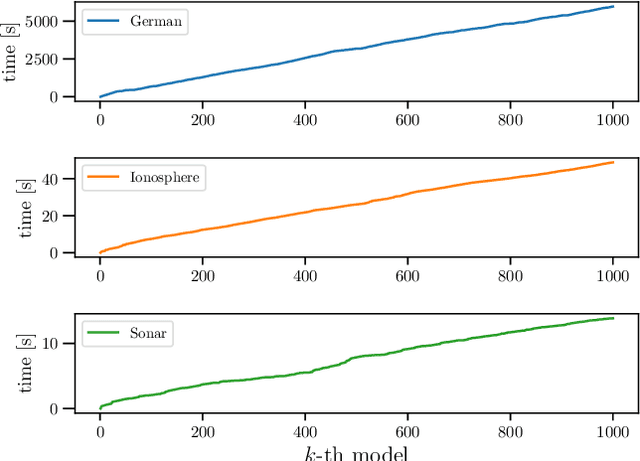
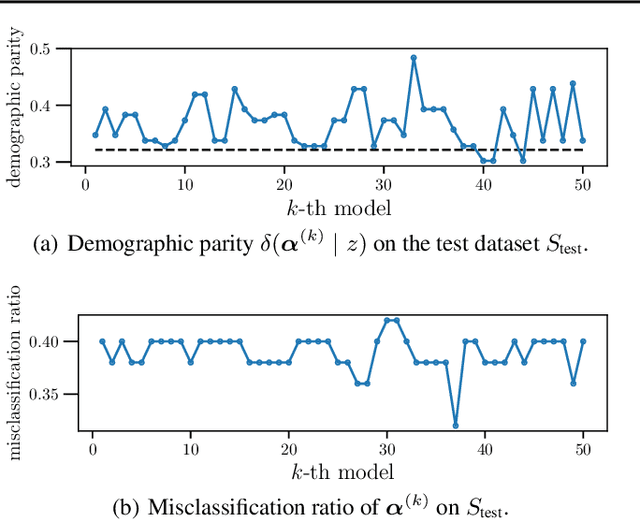
In conventional prediction tasks, a machine learning algorithm outputs a single best model that globally optimizes its objective function, which typically is accuracy. Therefore, users cannot access the other models explicitly. In contrast to this, multiple model enumeration attracts increasing interests in non-standard machine learning applications where other criteria, e.g., interpretability or fairness, than accuracy are main concern and a user may want to access more than one non-optimal, but suitable models. In this paper, we propose a K-best model enumeration algorithm for Support Vector Machines (SVM) that given a dataset S and an integer K>0, enumerates the K-best models on S with distinct support vectors in the descending order of the objective function values in the dual SVM problem. Based on analysis of the lattice structure of support vectors, our algorithm efficiently finds the next best model with small latency. This is useful in supporting users's interactive examination of their requirements on enumerated models. By experiments on real datasets, we evaluated the efficiency and usefulness of our algorithm.