A Constraint Programming Approach to Fair High School Course Scheduling

Issues of inequity in U.S. high schools' course scheduling did not previously exist. However, in recent years, with the increase in student population and course variety, students perceive that the course scheduling method is unfair. Current integer programming (IP) methods to the high school scheduling problem (HSSP) fall short in addressing these fairness concerns. The purpose of this research is to develop a solution methodology that generates feasible and fair course schedules using student preferences. Utilizing principles of fairness, which have been well studied in market design, we define the fair high school scheduling problem (FHSSP), a novel extension to the HSSP, and devise a corresponding algorithm based on integer programming to solve the FHSSP. We test our approach on a real course request dataset from a high school in California, USA. Results show that our algorithm can generate schedules that are both feasible and fair. In this paper, we demonstrate that our IP algorithm not only solves the HSSP and FHSSP in the United States but has the potential to be applied to various real-world scheduling problems. Additionally, we show the feasibility of integrating human emotions into mathematical modeling.

Enumeration of Distinct Support Vectors for Interactive Decision Making

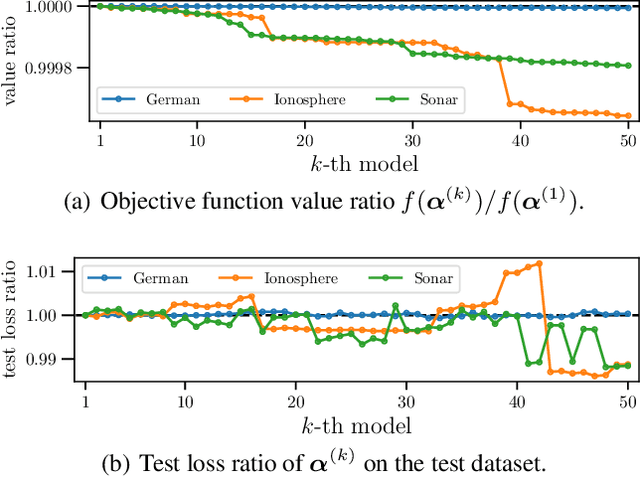
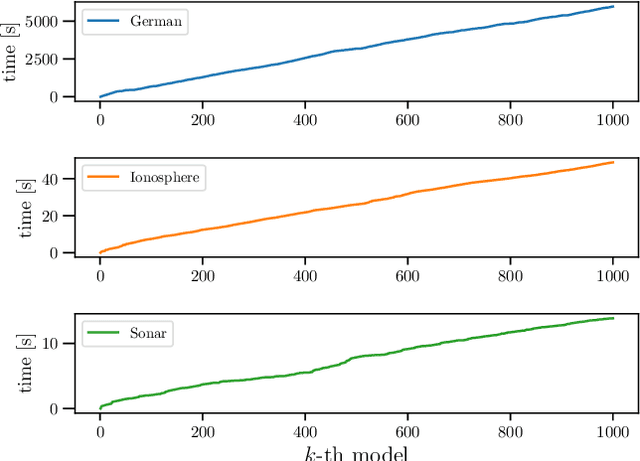
In conventional prediction tasks, a machine learning algorithm outputs a single best model that globally optimizes its objective function, which typically is accuracy. Therefore, users cannot access the other models explicitly. In contrast to this, multiple model enumeration attracts increasing interests in non-standard machine learning applications where other criteria, e.g., interpretability or fairness, than accuracy are main concern and a user may want to access more than one non-optimal, but suitable models. In this paper, we propose a K-best model enumeration algorithm for Support Vector Machines (SVM) that given a dataset S and an integer K>0, enumerates the K-best models on S with distinct support vectors in the descending order of the objective function values in the dual SVM problem. Based on analysis of the lattice structure of support vectors, our algorithm efficiently finds the next best model with small latency. This is useful in supporting users's interactive examination of their requirements on enumerated models. By experiments on real datasets, we evaluated the efficiency and usefulness of our algorithm.

Higher-Order Factorization Machines

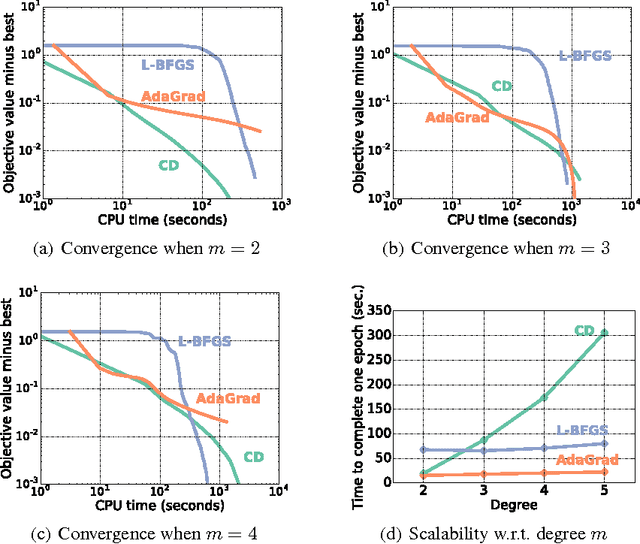
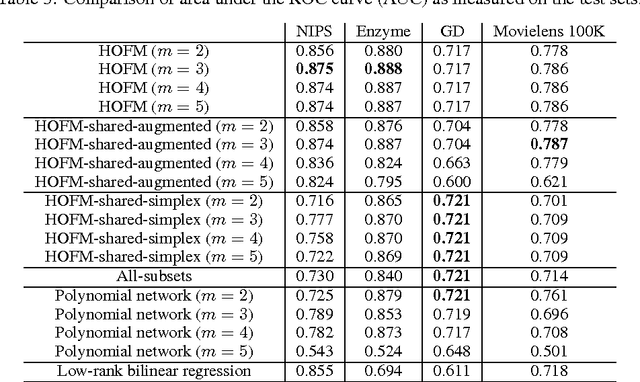
Factorization machines (FMs) are a supervised learning approach that can use second-order feature combinations even when the data is very high-dimensional. Unfortunately, despite increasing interest in FMs, there exists to date no efficient training algorithm for higher-order FMs (HOFMs). In this paper, we present the first generic yet efficient algorithms for training arbitrary-order HOFMs. We also present new variants of HOFMs with shared parameters, which greatly reduce model size and prediction times while maintaining similar accuracy. We demonstrate the proposed approaches on four different link prediction tasks.

Polynomial Networks and Factorization Machines: New Insights and Efficient Training Algorithms

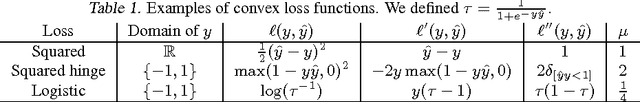
Polynomial networks and factorization machines are two recently-proposed models that can efficiently use feature interactions in classification and regression tasks. In this paper, we revisit both models from a unified perspective. Based on this new view, we study the properties of both models and propose new efficient training algorithms. Key to our approach is to cast parameter learning as a low-rank symmetric tensor estimation problem, which we solve by multi-convex optimization. We demonstrate our approach on regression and recommender system tasks.