Optimally Computing Compressed Indexing Arrays Based on the Compact Directed Acyclic Word Graph

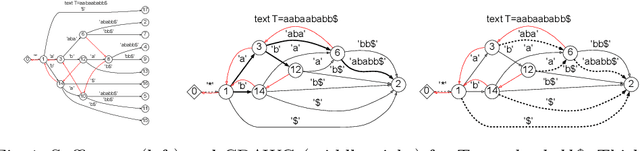
In this paper, we present the first study of the computational complexity of converting an automata-based text index structure, called the Compact Directed Acyclic Word Graph (CDAWG), of size $e$ for a text $T$ of length $n$ into other text indexing structures for the same text, suitable for highly repetitive texts: the run-length BWT of size $r$, the irreducible PLCP array of size $r$, and the quasi-irreducible LPF array of size $e$, as well as the lex-parse of size $O(r)$ and the LZ77-parse of size $z$, where $r, z \le e$. As main results, we showed that the above structures can be optimally computed from either the CDAWG for $T$ stored in read-only memory or its self-index version of size $e$ without a text in $O(e)$ worst-case time and words of working space. To obtain the above results, we devised techniques for enumerating a particular subset of suffixes in the lexicographic and text orders using the forward and backward search on the CDAWG by extending the results by Belazzougui et al. in 2015.

Computing the Collection of Good Models for Rule Lists

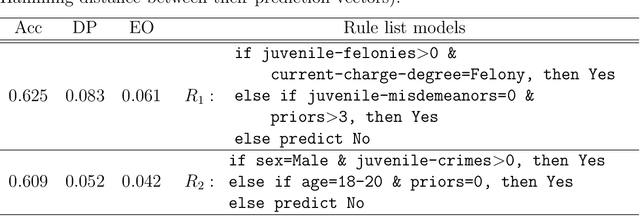
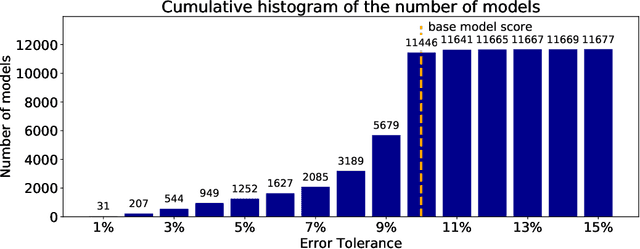
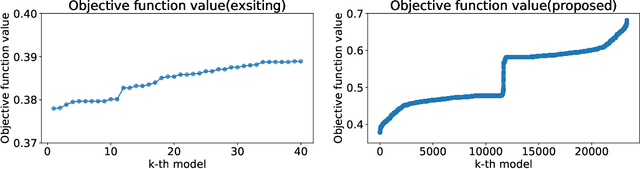
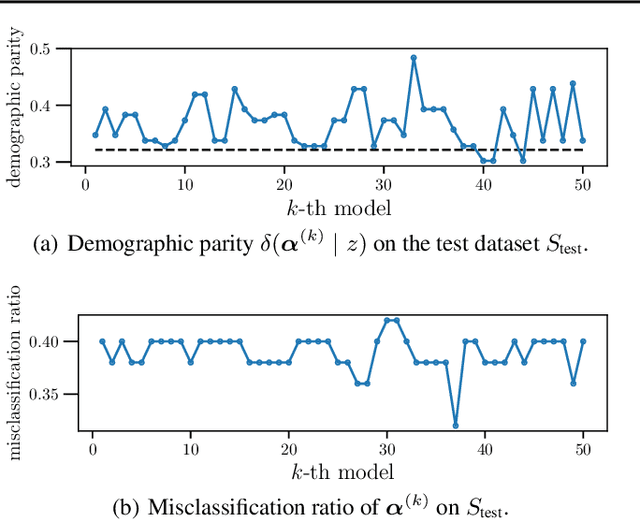
Since the seminal paper by Breiman in 2001, who pointed out a potential harm of prediction multiplicities from the view of explainable AI, global analysis of a collection of all good models, also known as a `Rashomon set,' has been attracted much attention for the last years. Since finding such a set of good models is a hard computational problem, there have been only a few algorithms for the problem so far, most of which are either approximate or incomplete. To overcome this difficulty, we study efficient enumeration of all good models for a subclass of interpretable models, called rule lists. Based on a state-of-the-art optimal rule list learner, CORELS, proposed by Angelino et al. in 2017, we present an efficient enumeration algorithm CorelsEnum for exactly computing a set of all good models using polynomial space in input size, given a dataset and a error tolerance from an optimal model. By experiments with the COMPAS dataset on recidivism prediction, our algorithm CorelsEnum successfully enumerated all of several tens of thousands of good rule lists of length at most $\ell = 3$ in around 1,000 seconds, while a state-of-the-art top-$K$ rule list learner based on Lawler's method combined with CORELS, proposed by Hara and Ishihata in 2018, found only 40 models until the timeout of 6,000 seconds. For global analysis, we conducted experiments for characterizing the Rashomon set, and observed large diversity of models in predictive multiplicity and fairness of models.

Ordered Counterfactual Explanation by Mixed-Integer Linear Optimization

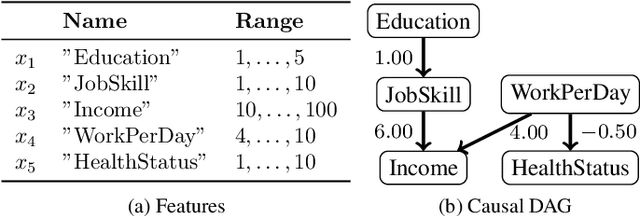
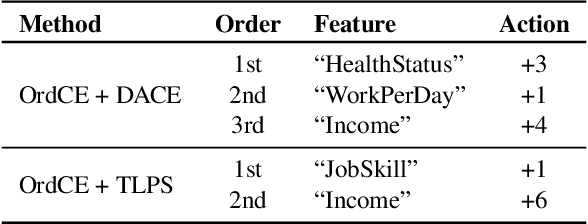
Post-hoc explanation methods for machine learning models have been widely used to support decision-making. One of the popular methods is Counterfactual Explanation (CE), which provides a user with a perturbation vector of features that alters the prediction result. Given a perturbation vector, a user can interpret it as an "action" for obtaining one's desired decision result. In practice, however, showing only a perturbation vector is often insufficient for users to execute the action. The reason is that if there is an asymmetric interaction among features, such as causality, the total cost of the action is expected to depend on the order of changing features. Therefore, practical CE methods are required to provide an appropriate order of changing features in addition to a perturbation vector. For this purpose, we propose a new framework called Ordered Counterfactual Explanation (OrdCE). We introduce a new objective function that evaluates a pair of an action and an order based on feature interaction. To extract an optimal pair, we propose a mixed-integer linear optimization approach with our objective function. Numerical experiments on real datasets demonstrated the effectiveness of our OrdCE in comparison with unordered CE methods.

Enumeration of Distinct Support Vectors for Interactive Decision Making

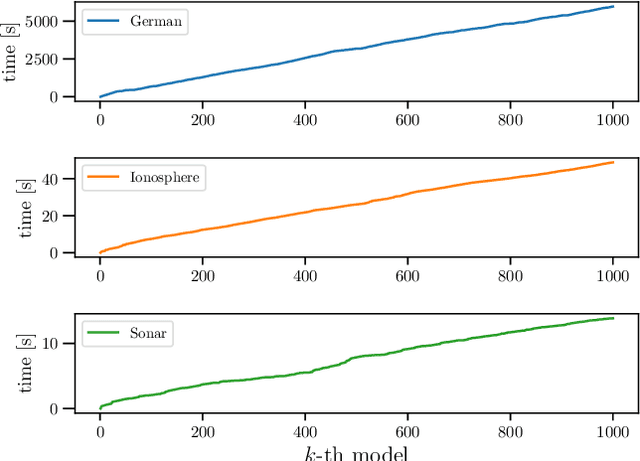
In conventional prediction tasks, a machine learning algorithm outputs a single best model that globally optimizes its objective function, which typically is accuracy. Therefore, users cannot access the other models explicitly. In contrast to this, multiple model enumeration attracts increasing interests in non-standard machine learning applications where other criteria, e.g., interpretability or fairness, than accuracy are main concern and a user may want to access more than one non-optimal, but suitable models. In this paper, we propose a K-best model enumeration algorithm for Support Vector Machines (SVM) that given a dataset S and an integer K>0, enumerates the K-best models on S with distinct support vectors in the descending order of the objective function values in the dual SVM problem. Based on analysis of the lattice structure of support vectors, our algorithm efficiently finds the next best model with small latency. This is useful in supporting users's interactive examination of their requirements on enumerated models. By experiments on real datasets, we evaluated the efficiency and usefulness of our algorithm.

On the Model Shrinkage Effect of Gamma Process Edge Partition Models

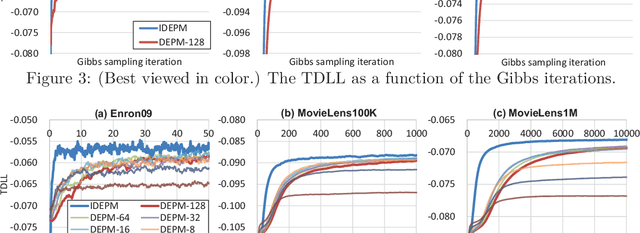
The edge partition model (EPM) is a fundamental Bayesian nonparametric model for extracting an overlapping structure from binary matrix. The EPM adopts a gamma process ($\Gamma$P) prior to automatically shrink the number of active atoms. However, we empirically found that the model shrinkage of the EPM does not typically work appropriately and leads to an overfitted solution. An analysis of the expectation of the EPM's intensity function suggested that the gamma priors for the EPM hyperparameters disturb the model shrinkage effect of the internal $\Gamma$P. In order to ensure that the model shrinkage effect of the EPM works in an appropriate manner, we proposed two novel generative constructions of the EPM: CEPM incorporating constrained gamma priors, and DEPM incorporating Dirichlet priors instead of the gamma priors. Furthermore, all DEPM's model parameters including the infinite atoms of the $\Gamma$P prior could be marginalized out, and thus it was possible to derive a truly infinite DEPM (IDEPM) that can be efficiently inferred using a collapsed Gibbs sampler. We experimentally confirmed that the model shrinkage of the proposed models works well and that the IDEPM indicated state-of-the-art performance in generalization ability, link prediction accuracy, mixing efficiency, and convergence speed.