Latent Conservative Objective Models for Data-Driven Crystal Structure Prediction

In computational chemistry, crystal structure prediction (CSP) is an optimization problem that involves discovering the lowest energy stable crystal structure for a given chemical formula. This problem is challenging as it requires discovering globally optimal designs with the lowest energies on complex manifolds. One approach to tackle this problem involves building simulators based on density functional theory (DFT) followed by running search in simulation, but these simulators are painfully slow. In this paper, we study present and study an alternate, data-driven approach to crystal structure prediction: instead of directly searching for the most stable structures in simulation, we train a surrogate model of the crystal formation energy from a database of existing crystal structures, and then optimize this model with respect to the parameters of the crystal structure. This surrogate model is trained to be conservative so as to prevent exploitation of its errors by the optimizer. To handle optimization in the non-Euclidean space of crystal structures, we first utilize a state-of-the-art graph diffusion auto-encoder (CD-VAE) to convert a crystal structure into a vector-based search space and then optimize a conservative surrogate model of the crystal energy, trained on top of this vector representation. We show that our approach, dubbed LCOMs (latent conservative objective models), performs comparably to the best current approaches in terms of success rate of structure prediction, while also drastically reducing computational cost.

On the Model Shrinkage Effect of Gamma Process Edge Partition Models

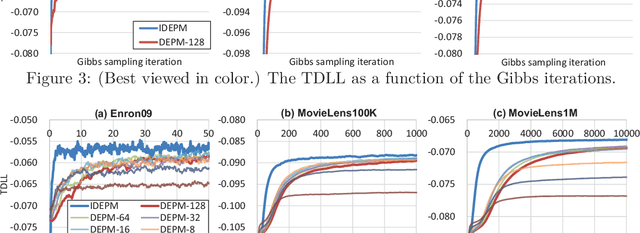
The edge partition model (EPM) is a fundamental Bayesian nonparametric model for extracting an overlapping structure from binary matrix. The EPM adopts a gamma process ($\Gamma$P) prior to automatically shrink the number of active atoms. However, we empirically found that the model shrinkage of the EPM does not typically work appropriately and leads to an overfitted solution. An analysis of the expectation of the EPM's intensity function suggested that the gamma priors for the EPM hyperparameters disturb the model shrinkage effect of the internal $\Gamma$P. In order to ensure that the model shrinkage effect of the EPM works in an appropriate manner, we proposed two novel generative constructions of the EPM: CEPM incorporating constrained gamma priors, and DEPM incorporating Dirichlet priors instead of the gamma priors. Furthermore, all DEPM's model parameters including the infinite atoms of the $\Gamma$P prior could be marginalized out, and thus it was possible to derive a truly infinite DEPM (IDEPM) that can be efficiently inferred using a collapsed Gibbs sampler. We experimentally confirmed that the model shrinkage of the proposed models works well and that the IDEPM indicated state-of-the-art performance in generalization ability, link prediction accuracy, mixing efficiency, and convergence speed.