Shunsuke Inenaga
Optimally Computing Compressed Indexing Arrays Based on the Compact Directed Acyclic Word Graph
Aug 04, 2023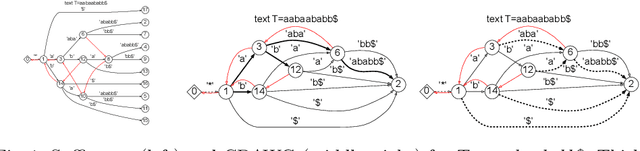

Abstract:In this paper, we present the first study of the computational complexity of converting an automata-based text index structure, called the Compact Directed Acyclic Word Graph (CDAWG), of size $e$ for a text $T$ of length $n$ into other text indexing structures for the same text, suitable for highly repetitive texts: the run-length BWT of size $r$, the irreducible PLCP array of size $r$, and the quasi-irreducible LPF array of size $e$, as well as the lex-parse of size $O(r)$ and the LZ77-parse of size $z$, where $r, z \le e$. As main results, we showed that the above structures can be optimally computed from either the CDAWG for $T$ stored in read-only memory or its self-index version of size $e$ without a text in $O(e)$ worst-case time and words of working space. To obtain the above results, we devised techniques for enumerating a particular subset of suffixes in the lexicographic and text orders using the forward and backward search on the CDAWG by extending the results by Belazzougui et al. in 2015.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge