Optimally Computing Compressed Indexing Arrays Based on the Compact Directed Acyclic Word Graph

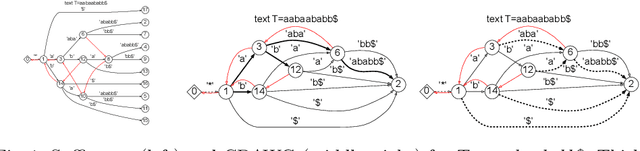
In this paper, we present the first study of the computational complexity of converting an automata-based text index structure, called the Compact Directed Acyclic Word Graph (CDAWG), of size $e$ for a text $T$ of length $n$ into other text indexing structures for the same text, suitable for highly repetitive texts: the run-length BWT of size $r$, the irreducible PLCP array of size $r$, and the quasi-irreducible LPF array of size $e$, as well as the lex-parse of size $O(r)$ and the LZ77-parse of size $z$, where $r, z \le e$. As main results, we showed that the above structures can be optimally computed from either the CDAWG for $T$ stored in read-only memory or its self-index version of size $e$ without a text in $O(e)$ worst-case time and words of working space. To obtain the above results, we devised techniques for enumerating a particular subset of suffixes in the lexicographic and text orders using the forward and backward search on the CDAWG by extending the results by Belazzougui et al. in 2015.

Computing Diverse Shortest Paths Efficiently: A Theoretical and Experimental Study

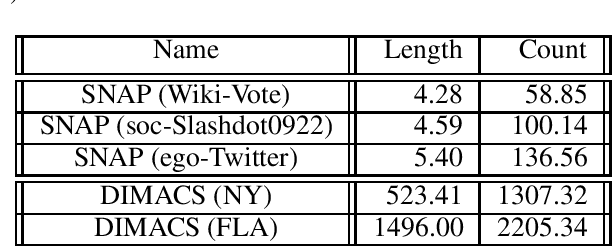
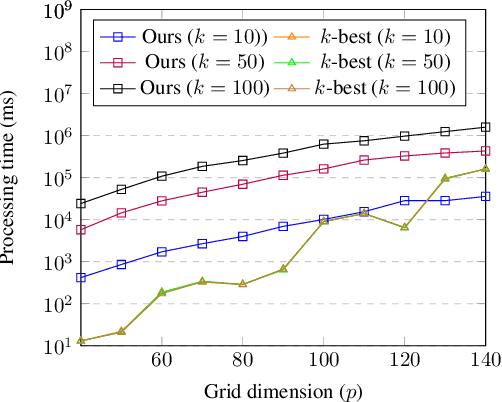
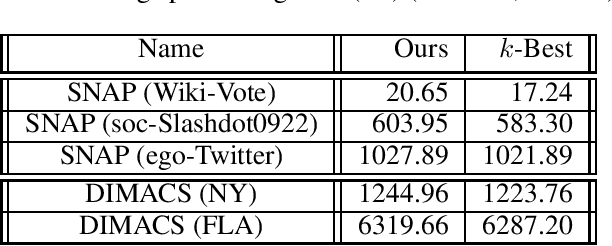
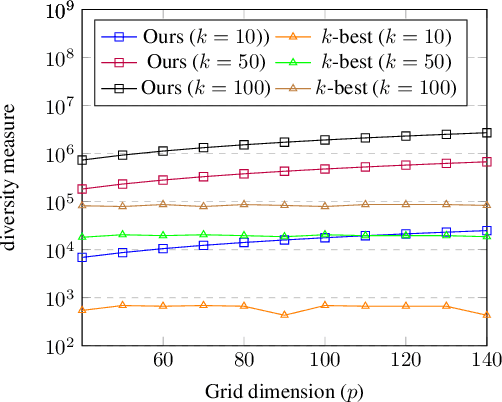
Finding diverse solutions in combinatorial problems recently has received considerable attention (Baste et al. 2020; Fomin et al. 2020; Hanaka et al. 2021). In this paper we study the following type of problems: given an integer $k$, the problem asks for $k$ solutions such that the sum of pairwise (weighted) Hamming distances between these solutions is maximized. Such solutions are called diverse solutions. We present a polynomial-time algorithm for finding diverse shortest $st$-paths in weighted directed graphs. Moreover, we study the diverse version of other classical combinatorial problems such as diverse weighted matroid bases, diverse weighted arborescences, and diverse bipartite matchings. We show that these problems can be solved in polynomial time as well. To evaluate the practical performance of our algorithm for finding diverse shortest $st$-paths, we conduct a computational experiment with synthetic and real-world instances.The experiment shows that our algorithm successfully computes diverse solutions within reasonable computational time.

Metric Learning for Ordered Labeled Trees with pq-grams

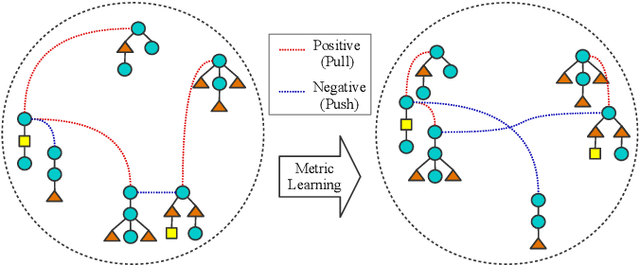
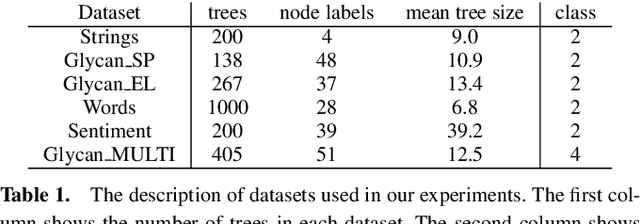
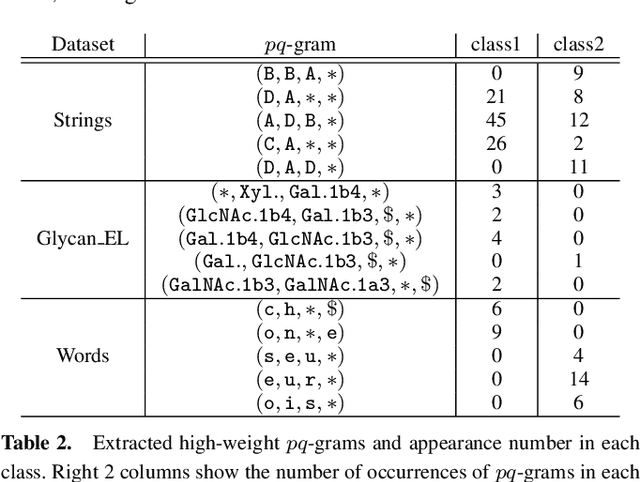
Computing the similarity between two data points plays a vital role in many machine learning algorithms. Metric learning has the aim of learning a good metric automatically from data. Most existing studies on metric learning for tree-structured data have adopted the approach of learning the tree edit distance. However, the edit distance is not amenable for big data analysis because it incurs high computation cost. In this paper, we propose a new metric learning approach for tree-structured data with pq-grams. The pq-gram distance is a distance for ordered labeled trees, and has much lower computation cost than the tree edit distance. In order to perform metric learning based on pq-grams, we propose a new differentiable parameterized distance, weighted pq-gram distance. We also propose a way to learn the proposed distance based on Large Margin Nearest Neighbors (LMNN), which is a well-studied and practical metric learning scheme. We formulate the metric learning problem as an optimization problem and use the gradient descent technique to perform metric learning. We empirically show that the proposed approach not only achieves competitive results with the state-of-the-art edit distance-based methods in various classification problems, but also solves the classification problems much more rapidly than the edit distance-based methods.

Automatic Source Code Summarization with Extended Tree-LSTM

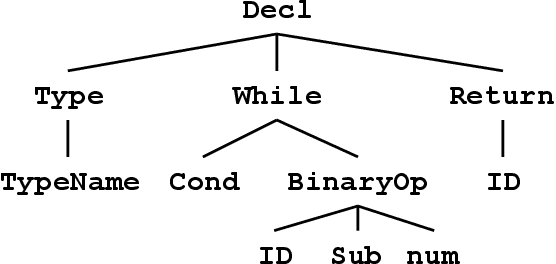
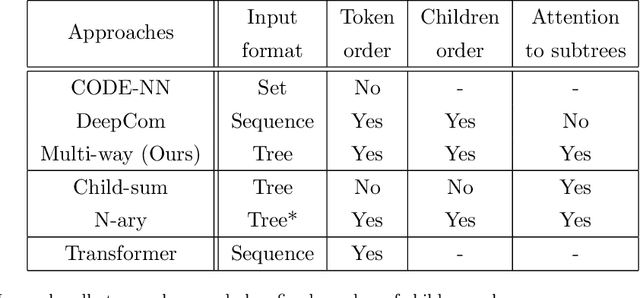
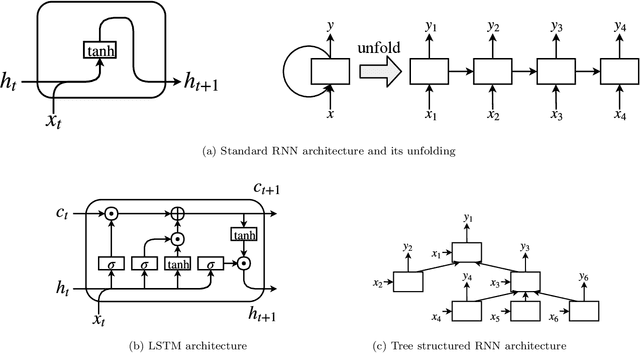
Neural machine translation models are used to automatically generate a document from given source code since this can be regarded as a machine translation task. Source code summarization is one of the components for automatic document generation, which generates a summary in natural language from given source code. This suggests that techniques used in neural machine translation, such as Long Short-Term Memory (LSTM), can be used for source code summarization. However, there is a considerable difference between source code and natural language: Source code is essentially {\em structured}, having loops and conditional branching, etc. Therefore, there is some obstacle to apply known machine translation models to source code. Abstract syntax trees (ASTs) capture these structural properties and play an important role in recent machine learning studies on source code. Tree-LSTM is proposed as a generalization of LSTMs for tree-structured data. However, there is a critical issue when applying it to ASTs: It cannot handle a tree that contains nodes having an arbitrary number of children and their order simultaneously, which ASTs generally have such nodes. To address this issue, we propose an extension of Tree-LSTM, which we call \emph{Multi-way Tree-LSTM} and apply it for source code summarization. As a result of computational experiments, our proposal achieved better results when compared with several state-of-the-art techniques.