Kazuhiro Kurita
Computing Diverse Shortest Paths Efficiently: A Theoretical and Experimental Study
Dec 15, 2021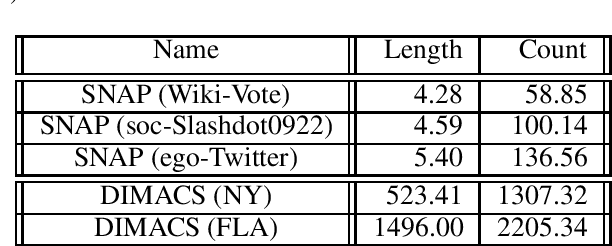
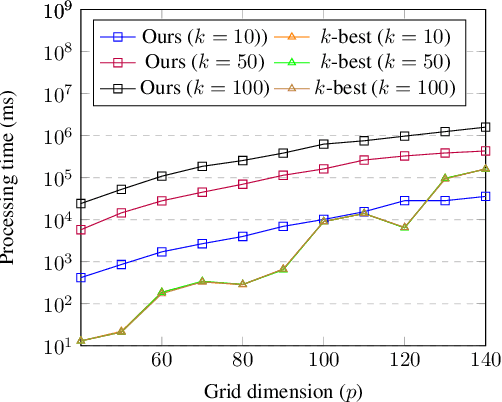
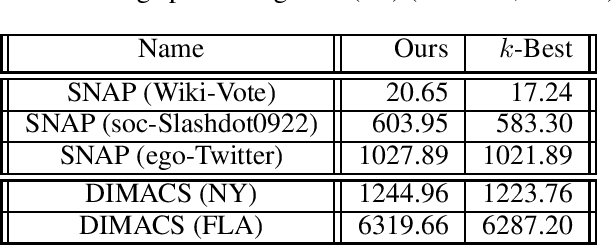
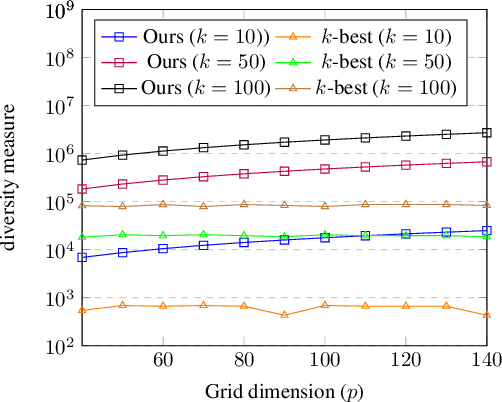
Abstract:Finding diverse solutions in combinatorial problems recently has received considerable attention (Baste et al. 2020; Fomin et al. 2020; Hanaka et al. 2021). In this paper we study the following type of problems: given an integer $k$, the problem asks for $k$ solutions such that the sum of pairwise (weighted) Hamming distances between these solutions is maximized. Such solutions are called diverse solutions. We present a polynomial-time algorithm for finding diverse shortest $st$-paths in weighted directed graphs. Moreover, we study the diverse version of other classical combinatorial problems such as diverse weighted matroid bases, diverse weighted arborescences, and diverse bipartite matchings. We show that these problems can be solved in polynomial time as well. To evaluate the practical performance of our algorithm for finding diverse shortest $st$-paths, we conduct a computational experiment with synthetic and real-world instances.The experiment shows that our algorithm successfully computes diverse solutions within reasonable computational time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge