Interior-Point Vanishing Problem in Semidefinite Relaxations for Neural Network Verification

Semidefinite programming (SDP) relaxation has emerged as a promising approach for neural network verification, offering tighter bounds than other convex relaxation methods for deep neural networks (DNNs) with ReLU activations. However, we identify a critical limitation in the SDP relaxation when applied to deep networks: interior-point vanishing, which leads to the loss of strict feasibility -- a crucial condition for the numerical stability and optimality of SDP. Through rigorous theoretical and empirical analysis, we demonstrate that as the depth of DNNs increases, the strict feasibility is likely to be lost, creating a fundamental barrier to scaling SDP-based verification. To address the interior-point vanishing, we design and investigate five solutions to enhance the feasibility conditions of the verification problem. Our methods can successfully solve 88% of the problems that could not be solved by existing methods, accounting for 41% of the total. Our analysis also reveals that the valid constraints for the lower and upper bounds for each ReLU unit are traditionally inherited from prior work without solid reasons, but are actually not only unbeneficial but also even harmful to the problem's feasibility. This work provides valuable insights into the fundamental challenges of SDP-based DNN verification and offers practical solutions to improve its applicability to deeper neural networks, contributing to the development of more reliable and secure systems with DNNs.

Learning Decision Trees and Forests with Algorithmic Recourse

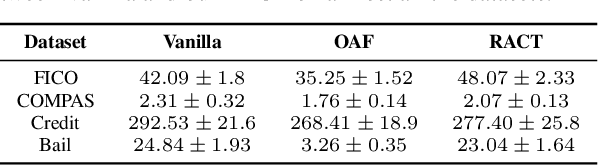
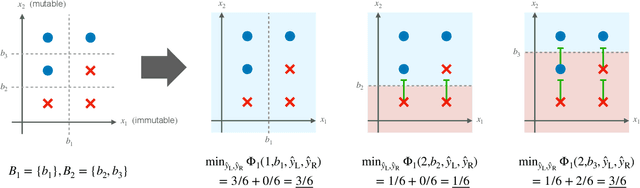
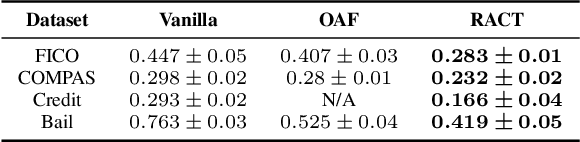
This paper proposes a new algorithm for learning accurate tree-based models while ensuring the existence of recourse actions. Algorithmic Recourse (AR) aims to provide a recourse action for altering the undesired prediction result given by a model. Typical AR methods provide a reasonable action by solving an optimization task of minimizing the required effort among executable actions. In practice, however, such actions do not always exist for models optimized only for predictive performance. To alleviate this issue, we formulate the task of learning an accurate classification tree under the constraint of ensuring the existence of reasonable actions for as many instances as possible. Then, we propose an efficient top-down greedy algorithm by leveraging the adversarial training techniques. We also show that our proposed algorithm can be applied to the random forest, which is known as a popular framework for learning tree ensembles. Experimental results demonstrated that our method successfully provided reasonable actions to more instances than the baselines without significantly degrading accuracy and computational efficiency.

SCOPE-RL: A Python Library for Offline Reinforcement Learning and Off-Policy Evaluation

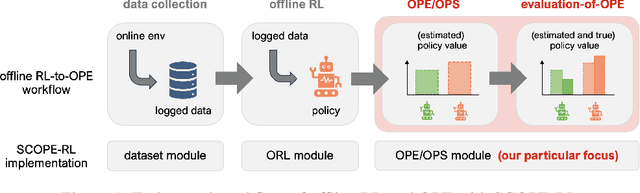
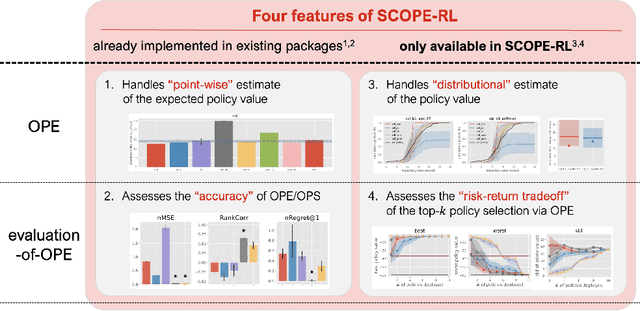
This paper introduces SCOPE-RL, a comprehensive open-source Python software designed for offline reinforcement learning (offline RL), off-policy evaluation (OPE), and selection (OPS). Unlike most existing libraries that focus solely on either policy learning or evaluation, SCOPE-RL seamlessly integrates these two key aspects, facilitating flexible and complete implementations of both offline RL and OPE processes. SCOPE-RL put particular emphasis on its OPE modules, offering a range of OPE estimators and robust evaluation-of-OPE protocols. This approach enables more in-depth and reliable OPE compared to other packages. For instance, SCOPE-RL enhances OPE by estimating the entire reward distribution under a policy rather than its mere point-wise expected value. Additionally, SCOPE-RL provides a more thorough evaluation-of-OPE by presenting the risk-return tradeoff in OPE results, extending beyond mere accuracy evaluations in existing OPE literature. SCOPE-RL is designed with user accessibility in mind. Its user-friendly APIs, comprehensive documentation, and a variety of easy-to-follow examples assist researchers and practitioners in efficiently implementing and experimenting with various offline RL methods and OPE estimators, tailored to their specific problem contexts. The documentation of SCOPE-RL is available at https://scope-rl.readthedocs.io/en/latest/.

Towards Assessing and Benchmarking Risk-Return Tradeoff of Off-Policy Evaluation

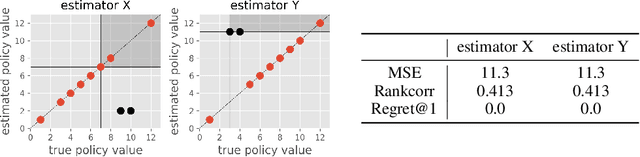
Off-Policy Evaluation (OPE) aims to assess the effectiveness of counterfactual policies using only offline logged data and is often used to identify the top-k promising policies for deployment in online A/B tests. Existing evaluation metrics for OPE estimators primarily focus on the "accuracy" of OPE or that of downstream policy selection, neglecting risk-return tradeoff in the subsequent online policy deployment. To address this issue, we draw inspiration from portfolio evaluation in finance and develop a new metric, called SharpeRatio@k, which measures the risk-return tradeoff of policy portfolios formed by an OPE estimator under varying online evaluation budgets (k). We validate our metric in two example scenarios, demonstrating its ability to effectively distinguish between low-risk and high-risk estimators and to accurately identify the most efficient estimator. This efficient estimator is characterized by its capability to form the most advantageous policy portfolios, maximizing returns while minimizing risks during online deployment, a nuance that existing metrics typically overlook. To facilitate a quick, accurate, and consistent evaluation of OPE via SharpeRatio@k, we have also integrated this metric into an open-source software, SCOPE-RL. Employing SharpeRatio@k and SCOPE-RL, we conduct comprehensive benchmarking experiments on various estimators and RL tasks, focusing on their risk-return tradeoff. These experiments offer several interesting directions and suggestions for future OPE research.

An IPW-based Unbiased Ranking Metric in Two-sided Markets

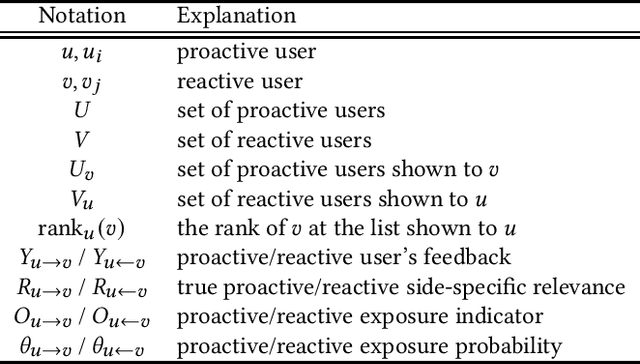
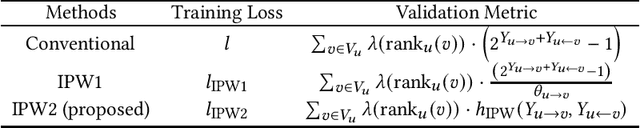
In modern recommendation systems, unbiased learning-to-rank (LTR) is crucial for prioritizing items from biased implicit user feedback, such as click data. Several techniques, such as Inverse Propensity Weighting (IPW), have been proposed for single-sided markets. However, less attention has been paid to two-sided markets, such as job platforms or dating services, where successful conversions require matching preferences from both users. This paper addresses the complex interaction of biases between users in two-sided markets and proposes a tailored LTR approach. We first present a formulation of feedback mechanisms in two-sided matching platforms and point out that their implicit feedback may include position bias from both user groups. On the basis of this observation, we extend the IPW estimator and propose a new estimator, named two-sided IPW, to address the position bases in two-sided markets. We prove that the proposed estimator satisfies the unbiasedness for the ground-truth ranking metric. We conducted numerical experiments on real-world two-sided platforms and demonstrated the effectiveness of our proposed method in terms of both precision and robustness. Our experiments showed that our method outperformed baselines especially when handling rare items, which are less frequently observed in the training data.

Counterfactual Explanation with Missing Values

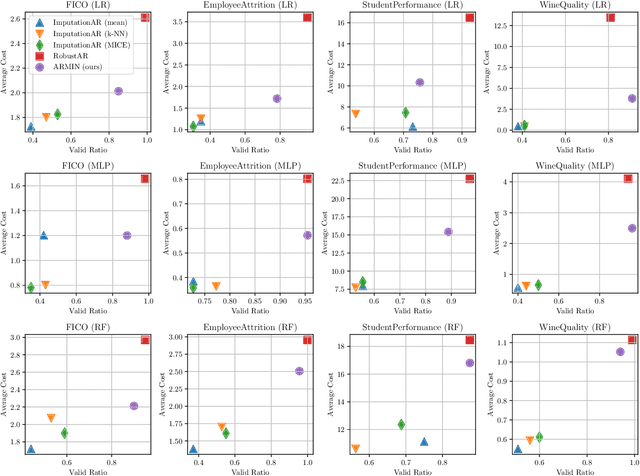
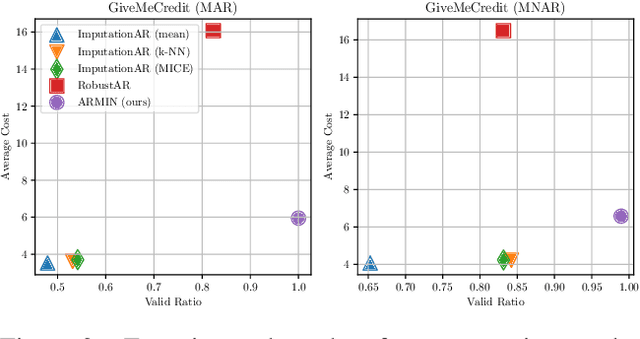
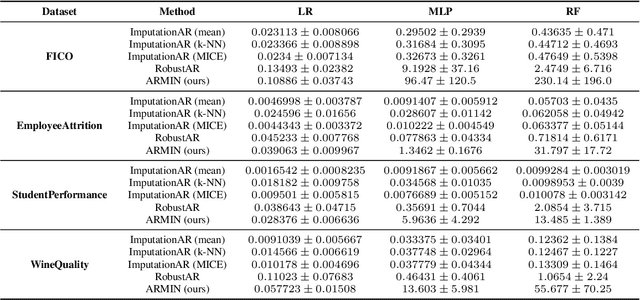
Counterfactual Explanation (CE) is a post-hoc explanation method that provides a perturbation for altering the prediction result of a classifier. Users can interpret the perturbation as an "action" to obtain their desired decision results. Existing CE methods require complete information on the features of an input instance. However, we often encounter missing values in a given instance, and the previous methods do not work in such a practical situation. In this paper, we first empirically and theoretically show the risk that missing value imputation methods affect the validity of an action, as well as the features that the action suggests changing. Then, we propose a new framework of CE, named Counterfactual Explanation by Pairs of Imputation and Action (CEPIA), that enables users to obtain valid actions even with missing values and clarifies how actions are affected by imputation of the missing values. Specifically, our CEPIA provides a representative set of pairs of an imputation candidate for a given incomplete instance and its optimal action. We formulate the problem of finding such a set as a submodular maximization problem, which can be solved by a simple greedy algorithm with an approximation guarantee. Experimental results demonstrated the efficacy of our CEPIA in comparison with the baselines in the presence of missing values.

Bézier Flow: a Surface-wise Gradient Descent Method for Multi-objective Optimization

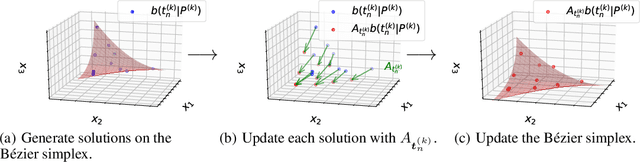
In this paper, we propose a strategy to construct a multi-objective optimization algorithm from a single-objective optimization algorithm by using the B\'ezier simplex model. Also, we extend the stability of optimization algorithms in the sense of Probability Approximately Correct (PAC) learning and define the PAC stability. We prove that it leads to an upper bound on the generalization with high probability. Furthermore, we show that multi-objective optimization algorithms derived from a gradient descent-based single-objective optimization algorithm are PAC stable. We conducted numerical experiments and demonstrated that our method achieved lower generalization errors than the existing multi-objective optimization algorithm.

A Two-phase Framework with a Bézier Simplex-based Interpolation Method for Computationally Expensive Multi-objective Optimization

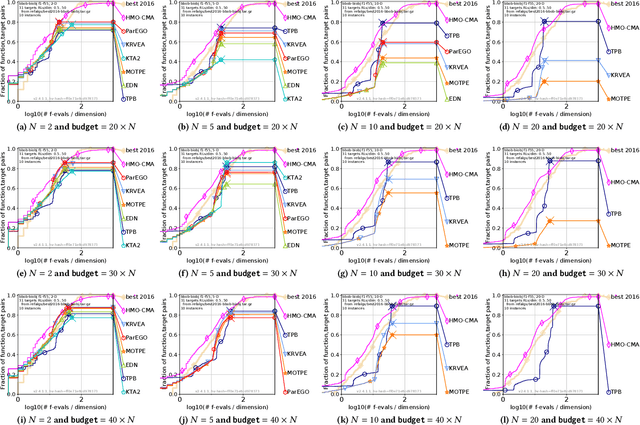
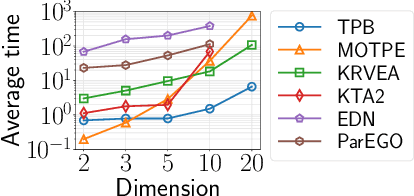
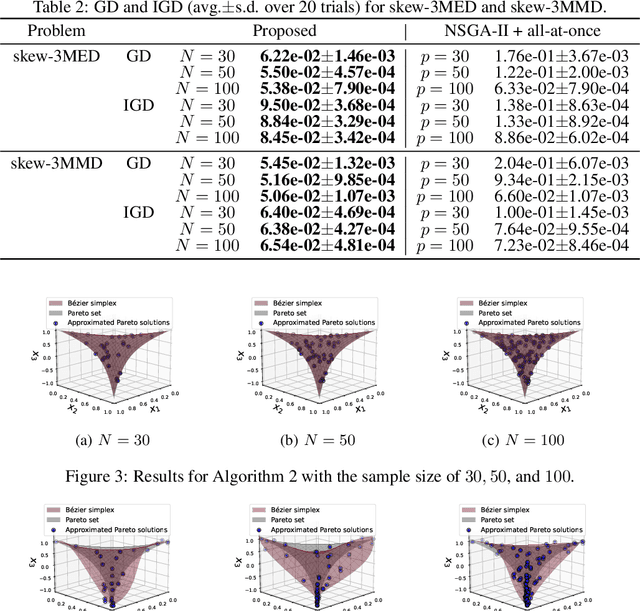
This paper proposes a two-phase framework with a B\'{e}zier simplex-based interpolation method (TPB) for computationally expensive multi-objective optimization. The first phase in TPB aims to approximate a few Pareto optimal solutions by optimizing a sequence of single-objective scalar problems. The first phase in TPB can fully exploit a state-of-the-art single-objective derivative-free optimizer. The second phase in TPB utilizes a B\'{e}zier simplex model to interpolate the solutions obtained in the first phase. The second phase in TPB fully exploits the fact that a B\'{e}zier simplex model can approximate the Pareto optimal solution set by exploiting its simplex structure when a given problem is simplicial. We investigate the performance of TPB on the 55 bi-objective BBOB problems. The results show that TPB performs significantly better than HMO-CMA-ES and some state-of-the-art meta-model-based optimizers.

Approximate Bayesian Computation of Bézier Simplices

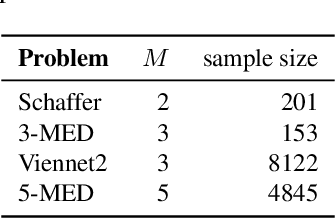
B\'ezier simplex fitting algorithms have been recently proposed to approximate the Pareto set/front of multi-objective continuous optimization problems. These new methods have shown to be successful at approximating various shapes of Pareto sets/fronts when sample points exactly lie on the Pareto set/front. However, if the sample points scatter away from the Pareto set/front, those methods often likely suffer from over-fitting. To overcome this issue, in this paper, we extend the B\'ezier simplex model to a probabilistic one and propose a new learning algorithm of it, which falls into the framework of approximate Bayesian computation (ABC) based on the Wasserstein distance. We also study the convergence property of the Wasserstein ABC algorithm. An extensive experimental evaluation on publicly available problem instances shows that the new algorithm converges on a finite sample. Moreover, it outperforms the deterministic fitting methods on noisy instances.

Ordered Counterfactual Explanation by Mixed-Integer Linear Optimization

Post-hoc explanation methods for machine learning models have been widely used to support decision-making. One of the popular methods is Counterfactual Explanation (CE), which provides a user with a perturbation vector of features that alters the prediction result. Given a perturbation vector, a user can interpret it as an "action" for obtaining one's desired decision result. In practice, however, showing only a perturbation vector is often insufficient for users to execute the action. The reason is that if there is an asymmetric interaction among features, such as causality, the total cost of the action is expected to depend on the order of changing features. Therefore, practical CE methods are required to provide an appropriate order of changing features in addition to a perturbation vector. For this purpose, we propose a new framework called Ordered Counterfactual Explanation (OrdCE). We introduce a new objective function that evaluates a pair of an action and an order based on feature interaction. To extract an optimal pair, we propose a mixed-integer linear optimization approach with our objective function. Numerical experiments on real datasets demonstrated the effectiveness of our OrdCE in comparison with unordered CE methods.