Analyzing the Landscape of the Indicator-based Subset Selection Problem

The indicator-based subset selection problem (ISSP) involves finding a point subset that minimizes or maximizes a quality indicator. The ISSP is frequently found in evolutionary multi-objective optimization (EMO). An in-depth understanding of the landscape of the ISSP could be helpful in developing efficient subset selection methods and explaining their performance. However, the landscape of the ISSP is poorly understood. To address this issue, this paper analyzes the landscape of the ISSP by using various traditional landscape analysis measures and exact local optima networks (LONs). This paper mainly investigates how the landscape of the ISSP is influenced by the choice of a quality indicator and the shape of the Pareto front. Our findings provide insightful information about the ISSP. For example, high neutrality and many local optima are observed in the results for ISSP instances with the additive $\epsilon$-indicator.

Speeding up Local Search for the Indicator-based Subset Selection Problem by a Candidate List Strategy

In evolutionary multi-objective optimization, the indicator-based subset selection problem involves finding a subset of points that maximizes a given quality indicator. Local search is an effective approach for obtaining a high-quality subset in this problem. However, local search requires high computational cost, especially as the size of the point set and the number of objectives increase. To address this issue, this paper proposes a candidate list strategy for local search in the indicator-based subset selection problem. In the proposed strategy, each point in a given point set has a candidate list. During search, each point is only eligible to swap with unselected points in its associated candidate list. This restriction drastically reduces the number of swaps at each iteration of local search. We consider two types of candidate lists: nearest neighbor and random neighbor lists. This paper investigates the effectiveness of the proposed candidate list strategy on various Pareto fronts. The results show that the proposed strategy with the nearest neighbor list can significantly speed up local search on continuous Pareto fronts without significantly compromising the subset quality. The results also show that the sequential use of the two lists can address the discontinuity of Pareto fronts.

Benchmarking Parameter Control Methods in Differential Evolution for Mixed-Integer Black-Box Optimization

Differential evolution (DE) generally requires parameter control methods (PCMs) for the scale factor and crossover rate. Although a better understanding of PCMs provides a useful clue to designing an efficient DE, their effectiveness is poorly understood in mixed-integer black-box optimization. In this context, this paper benchmarks PCMs in DE on the mixed-integer black-box optimization benchmarking function (bbob-mixint) suite in a component-wise manner. First, we demonstrate that the best PCM significantly depends on the combination of the mutation strategy and repair method. Although the PCM of SHADE is state-of-the-art for numerical black-box optimization, our results show its poor performance for mixed-integer black-box optimization. In contrast, our results show that some simple PCMs (e.g., the PCM of CoDE) perform the best in most cases. Then, we demonstrate that a DE with a suitable PCM performs significantly better than CMA-ES with integer handling for larger budgets of function evaluations. Finally, we show how the adaptation in the PCM of SHADE fails.

Investigating Normalization in Preference-based Evolutionary Multi-objective Optimization Using a Reference Point

Normalization of objectives plays a crucial role in evolutionary multi-objective optimization (EMO) to handle objective functions with different scales, which can be found in real-world problems. Although the effect of normalization methods on the performance of EMO algorithms has been investigated in the literature, that of preference-based EMO (PBEMO) algorithms is poorly understood. Since PBEMO aims to approximate a region of interest, its population generally does not cover the Pareto front in the objective space. This property may make normalization of objectives in PBEMO difficult. This paper investigates the effectiveness of three normalization methods in three representative PBEMO algorithms. We present a bounded archive-based method for approximating the nadir point. First, we demonstrate that the normalization methods in PBEMO perform significantly worse than that in conventional EMO in terms of approximating the ideal point, nadir point, and range of the PF. Then, we show that PBEMO requires normalization of objectives on problems with differently scaled objectives. Our results show that there is no clear "best normalization method" in PBEMO, but an external archive-based method performs relatively well.

On the Unbounded External Archive and Population Size in Preference-based Evolutionary Multi-objective Optimization Using a Reference Point

Although the population size is an important parameter in evolutionary multi-objective optimization (EMO), little is known about its influence on preference-based EMO (PBEMO). The effectiveness of an unbounded external archive (UA) in PBEMO is also poorly understood, where the UA maintains all non-dominated solutions found so far. In addition, existing methods for postprocessing the UA cannot handle the decision maker's preference information. In this context, first, this paper proposes a preference-based postprocessing method for selecting representative solutions from the UA. Then, we investigate the influence of the UA and population size on the performance of PBEMO algorithms. Our results show that the performance of PBEMO algorithms (e.g., R-NSGA-II) can be significantly improved by using the UA and the proposed method. We demonstrate that a smaller population size than commonly used is effective in most PBEMO algorithms for a small budget of function evaluations, even for many objectives. We found that the size of the region of interest is a less important factor in selecting the population size of the PBEMO algorithms on real-world problems.

Quality Indicators for Preference-based Evolutionary Multi-objective Optimization Using a Reference Point: A Review and Analysis

Some quality indicators have been proposed for benchmarking preference-based evolutionary multi-objective optimization algorithms using a reference point. Although a systematic review and analysis of the quality indicators are helpful for both benchmarking and practical decision-making, neither has been conducted. In this context, first, this paper reviews existing regions of interest and quality indicators for preference-based evolutionary multi-objective optimization using the reference point. We point out that each quality indicator was designed for a different region of interest. Then, this paper investigates the properties of the quality indicators. We demonstrate that an achievement scalarizing function value is not always consistent with the distance from a solution to the reference point in the objective space. We observe that the regions of interest can be significantly different depending on the position of the reference point and the shape of the Pareto front. We identify undesirable properties of some quality indicators. We also show that the ranking of preference-based evolutionary multi-objective optimization algorithms significantly depends on the choice of quality indicators.

Benchmarking the Hooke-Jeeves Method, MTS-LS1, and BSrr on the Large-scale BBOB Function Set

This paper investigates the performance of three black-box optimizers exploiting separability on the 24 large-scale BBOB functions, including the Hooke-Jeeves method, MTS-LS1, and BSrr. Although BSrr was not specially designed for large-scale optimization, the results show that BSrr has a state-of-the-art performance on the five separable large-scale BBOB functions. The results show that the asymmetry significantly influences the performance of MTS-LS1. The results also show that the Hooke-Jeeves method performs better than MTS-LS1 on unimodal separable BBOB functions.

A Two-phase Framework with a Bézier Simplex-based Interpolation Method for Computationally Expensive Multi-objective Optimization

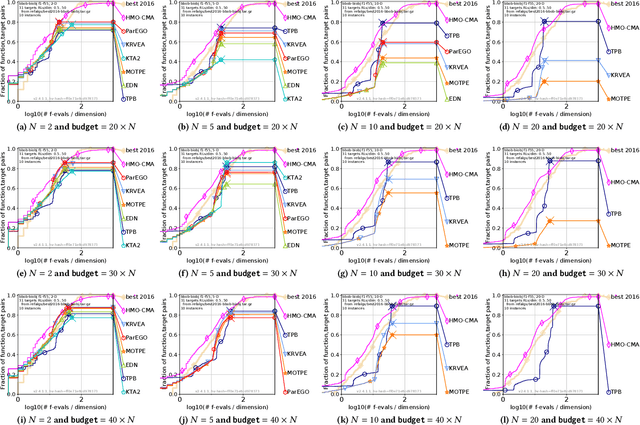
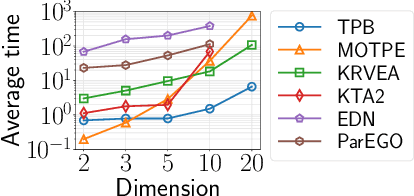
This paper proposes a two-phase framework with a B\'{e}zier simplex-based interpolation method (TPB) for computationally expensive multi-objective optimization. The first phase in TPB aims to approximate a few Pareto optimal solutions by optimizing a sequence of single-objective scalar problems. The first phase in TPB can fully exploit a state-of-the-art single-objective derivative-free optimizer. The second phase in TPB utilizes a B\'{e}zier simplex model to interpolate the solutions obtained in the first phase. The second phase in TPB fully exploits the fact that a B\'{e}zier simplex model can approximate the Pareto optimal solution set by exploiting its simplex structure when a given problem is simplicial. We investigate the performance of TPB on the 55 bi-objective BBOB problems. The results show that TPB performs significantly better than HMO-CMA-ES and some state-of-the-art meta-model-based optimizers.

Benchmarking Feature-based Algorithm Selection Systems for Black-box Numerical Optimization

Feature-based algorithm selection aims to automatically find the best one from a portfolio of optimization algorithms on an unseen problem based on its landscape features. Feature-based algorithm selection has recently received attention in the research field of black-box numerical optimization. However, algorithm selection for black-box optimization has been poorly understood. Most previous studies have focused only on whether an algorithm selection system can outperform the single-best solver in a portfolio. In addition, a benchmarking methodology for algorithm selection systems has not been well investigated in the literature. In this context, this paper analyzes algorithm selection systems on the 24 noiseless black-box optimization benchmarking functions. First, we demonstrate that the successful performance 1 measure is more reliable than the expected runtime measure for benchmarking algorithm selection systems. Then, we examine the influence of randomness on the performance of algorithm selection systems. We also show that the performance of algorithm selection systems can be significantly improved by using a pre-solver. We point out that the difficulty of outperforming the single-best solver depends on algorithm portfolios, cross-validation methods, and dimensions. Finally, we demonstrate that the effectiveness of algorithm portfolios depends on various factors. These findings provide fundamental insights for algorithm selection for black-box optimization.

Towards Exploratory Landscape Analysis for Large-scale Optimization: A Dimensionality Reduction Framework

Although exploratory landscape analysis (ELA) has shown its effectiveness in various applications, most previous studies focused only on low- and moderate-dimensional problems. Thus, little is known about the scalability of the ELA approach for large-scale optimization. In this context, first, this paper analyzes the computational cost of features in the flacco package. Our results reveal that two important feature classes (ela_level and ela_meta) cannot be applied to large-scale optimization due to their high computational cost. To improve the scalability of the ELA approach, this paper proposes a dimensionality reduction framework that computes features in a reduced lower-dimensional space than the original solution space. We demonstrate that the proposed framework can drastically reduce the computation time of ela_level and ela_meta for large dimensions. In addition, the proposed framework can make the cell-mapping feature classes scalable for large-scale optimization. Our results also show that features computed by the proposed framework are beneficial for predicting the high-level properties of the 24 large-scale BBOB functions.