Bézier Flow: a Surface-wise Gradient Descent Method for Multi-objective Optimization

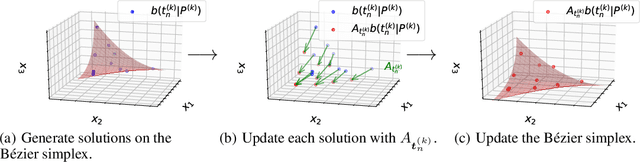
In this paper, we propose a strategy to construct a multi-objective optimization algorithm from a single-objective optimization algorithm by using the B\'ezier simplex model. Also, we extend the stability of optimization algorithms in the sense of Probability Approximately Correct (PAC) learning and define the PAC stability. We prove that it leads to an upper bound on the generalization with high probability. Furthermore, we show that multi-objective optimization algorithms derived from a gradient descent-based single-objective optimization algorithm are PAC stable. We conducted numerical experiments and demonstrated that our method achieved lower generalization errors than the existing multi-objective optimization algorithm.

A Two-phase Framework with a Bézier Simplex-based Interpolation Method for Computationally Expensive Multi-objective Optimization

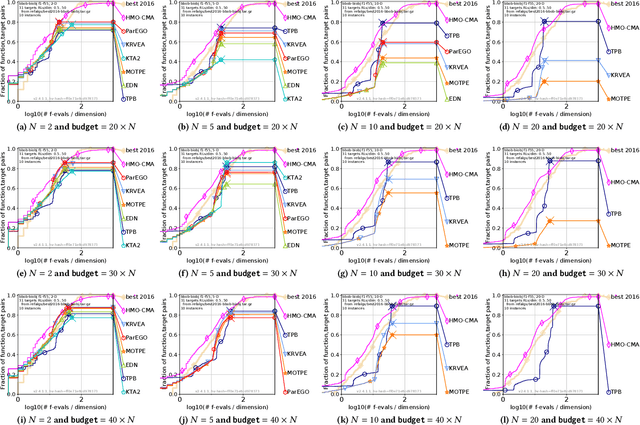
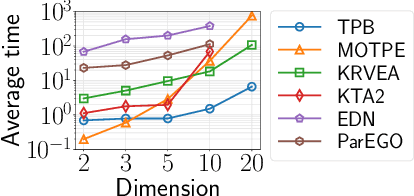
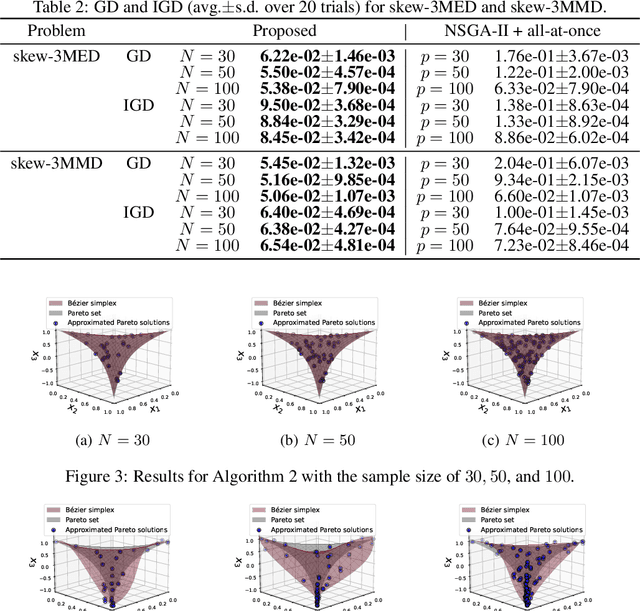
This paper proposes a two-phase framework with a B\'{e}zier simplex-based interpolation method (TPB) for computationally expensive multi-objective optimization. The first phase in TPB aims to approximate a few Pareto optimal solutions by optimizing a sequence of single-objective scalar problems. The first phase in TPB can fully exploit a state-of-the-art single-objective derivative-free optimizer. The second phase in TPB utilizes a B\'{e}zier simplex model to interpolate the solutions obtained in the first phase. The second phase in TPB fully exploits the fact that a B\'{e}zier simplex model can approximate the Pareto optimal solution set by exploiting its simplex structure when a given problem is simplicial. We investigate the performance of TPB on the 55 bi-objective BBOB problems. The results show that TPB performs significantly better than HMO-CMA-ES and some state-of-the-art meta-model-based optimizers.

GenéLive! Generating Rhythm Actions in Love Live!

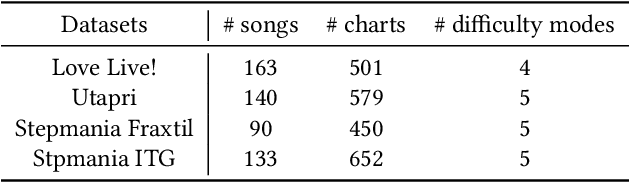
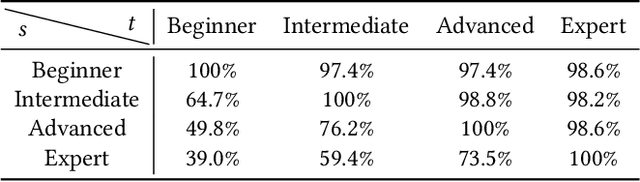
A rhythm action game is a music-based video game in which the player is challenged to issue commands at the right timings during a music session. The timings are rendered in the chart, which consists of visual symbols, called notes, flying through the screen. KLab Inc., a Japan-based video game developer, has operated rhythm action games including a title for the "Love Live!" franchise, which became a hit across Asia and beyond. Before this work, the company generated the charts manually, which resulted in a costly business operation. This paper presents how KLab applied a deep generative model for synthesizing charts, and shows how it has improved the chart production process, reducing the business cost by half. Existing generative models generated poor quality charts for easier difficulty modes. We report how we overcame this challenge through a multi-scaling model dedicated to rhythm actions, by considering beats among other things. Our model, named Gen\'eLive!, is evaluated using production datasets at KLab as well as open datasets.

Explicitly Multi-Modal Benchmarks for Multi-Objective Optimization

We model multi-modality in multi-objective optimization problems and apply this to generate benchmarking problems. In the model, the mode is based on the singularity of the objective functions.

All unconstrained strongly convex problems are weakly simplicial

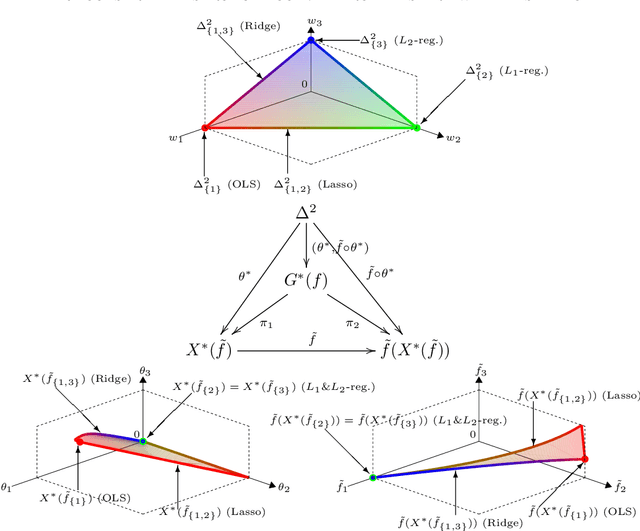
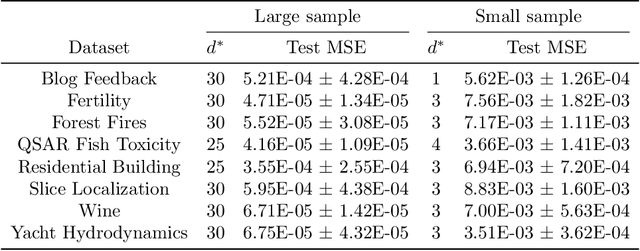
A multi-objective optimization problem is $C^r$ weakly simplicial if there exists a $C^r$ surjection from a simplex onto the Pareto set/front such that the image of each subsimplex is the Pareto set/front of a subproblem, where $0\leq r\leq \infty$. This property is helpful to compute a parametric-surface approximation of the entire Pareto set and Pareto front. It is known that all unconstrained strongly convex $C^r$ problems are $C^{r-1}$ weakly simplicial for $1\leq r \leq \infty$. In this paper, we show that all unconstrained strongly convex problems are $C^0$ weakly simplicial. The usefulness of this theorem is demonstrated in a sparse modeling application: we reformulate the elastic net as a non-differentiable multi-objective strongly convex problem and approximate its Pareto set (the set of all trained models with different hyper-parameters) and Pareto front (the set of performance metrics of the trained models) by using a B\'ezier simplex fitting method, which accelerates hyper-parameter search.

Approximate Bayesian Computation of Bézier Simplices

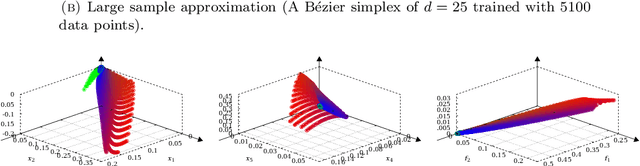
B\'ezier simplex fitting algorithms have been recently proposed to approximate the Pareto set/front of multi-objective continuous optimization problems. These new methods have shown to be successful at approximating various shapes of Pareto sets/fronts when sample points exactly lie on the Pareto set/front. However, if the sample points scatter away from the Pareto set/front, those methods often likely suffer from over-fitting. To overcome this issue, in this paper, we extend the B\'ezier simplex model to a probabilistic one and propose a new learning algorithm of it, which falls into the framework of approximate Bayesian computation (ABC) based on the Wasserstein distance. We also study the convergence property of the Wasserstein ABC algorithm. An extensive experimental evaluation on publicly available problem instances shows that the new algorithm converges on a finite sample. Moreover, it outperforms the deterministic fitting methods on noisy instances.

Asymptotic Risk of Bezier Simplex Fitting

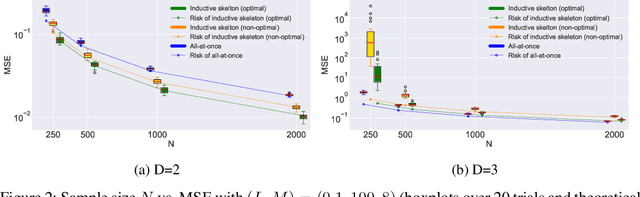
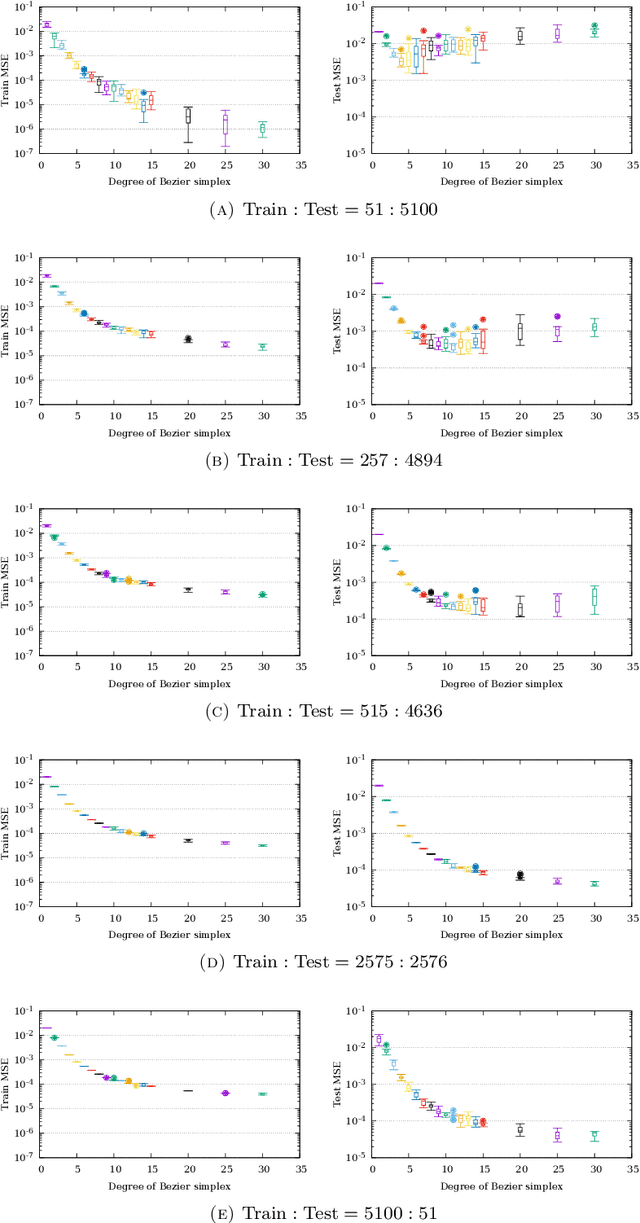
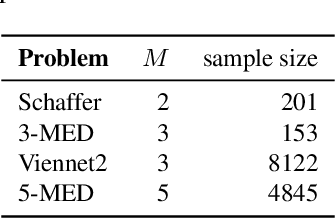
The Bezier simplex fitting is a novel data modeling technique which exploits geometric structures of data to approximate the Pareto front of multi-objective optimization problems. There are two fitting methods based on different sampling strategies. The inductive skeleton fitting employs a stratified subsampling from each skeleton of a simplex, whereas the all-at-once fitting uses a non-stratified sampling which treats a simplex as a whole. In this paper, we analyze the asymptotic risks of those B\'ezier simplex fitting methods and derive the optimal subsample ratio for the inductive skeleton fitting. It is shown that the inductive skeleton fitting with the optimal ratio has a smaller risk when the degree of a Bezier simplex is less than three. Those results are verified numerically under small to moderate sample sizes. In addition, we provide two complementary applications of our theory: a generalized location problem and a multi-objective hyper-parameter tuning of the group lasso. The former can be represented by a Bezier simplex of degree two where the inductive skeleton fitting outperforms. The latter can be represented by a Bezier simplex of degree three where the all-at-once fitting gets an advantage.

Data-Driven Analysis of Pareto Set Topology

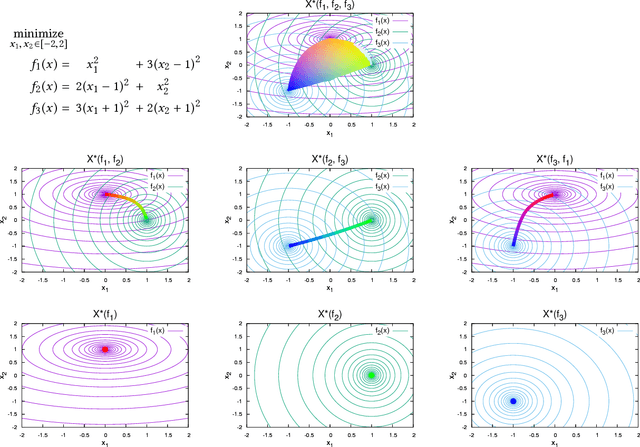
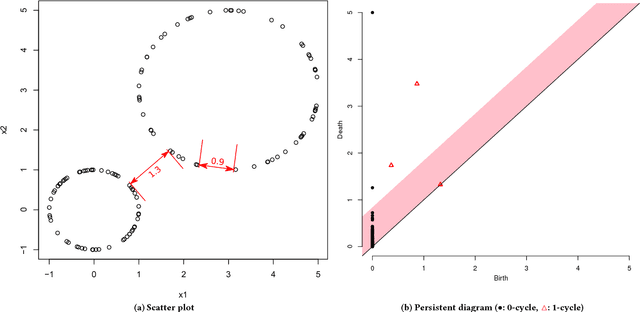
When and why can evolutionary multi-objective optimization (EMO) algorithms cover the entire Pareto set? That is a major concern for EMO researchers and practitioners. A recent theoretical study revealed that (roughly speaking) if the Pareto set forms a topological simplex (a curved line, a curved triangle, a curved tetrahedron, etc.), then decomposition-based EMO algorithms can cover the entire Pareto set. Usually, we cannot know the true Pareto set and have to estimate its topology by using the population of EMO algorithms during or after the runtime. This paper presents a data-driven approach to analyze the topology of the Pareto set. We give a theory of how to recognize the topology of the Pareto set from data and implement an algorithm to judge whether the true Pareto set may form a topological simplex or not. Numerical experiments show that the proposed method correctly recognizes the topology of high-dimensional Pareto sets within reasonable population size.

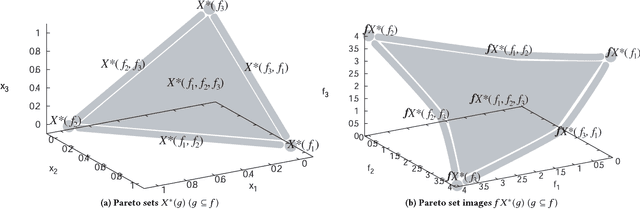
Simple Problems: The Simplicial Gluing Structure of Pareto Sets and Pareto Fronts

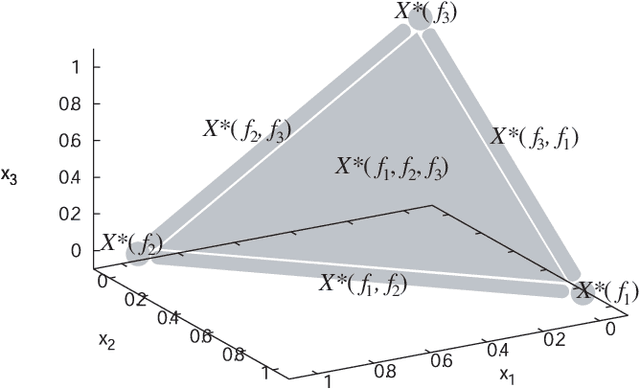
Quite a few studies on real-world applications of multi-objective optimization reported that their Pareto sets and Pareto fronts form a topological simplex. Such a class of problems was recently named the simple problems, and their Pareto set and Pareto front were observed to have a gluing structure similar to the faces of a simplex. This paper gives a theoretical justification for that observation by proving the gluing structure of the Pareto sets/fronts of subproblems of a simple problem. The simplicity of standard benchmark problems is studied.

Population Synthesis via k-Nearest Neighbor Crossover Kernel

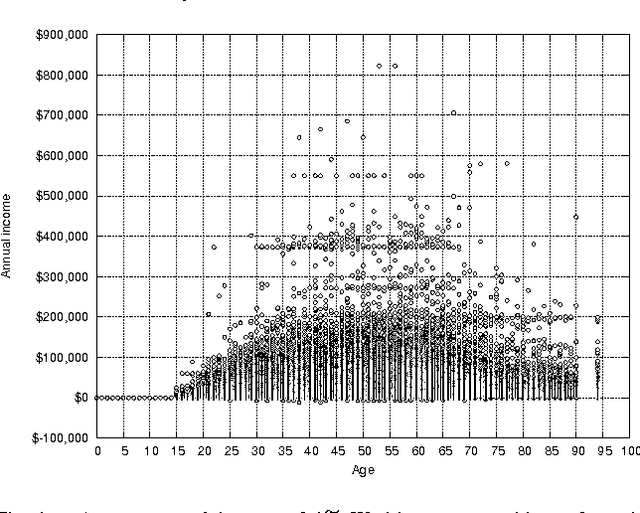
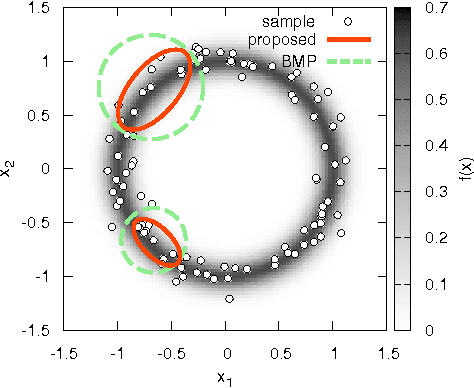
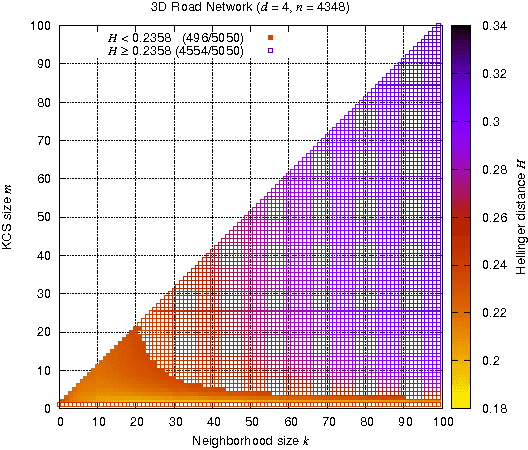
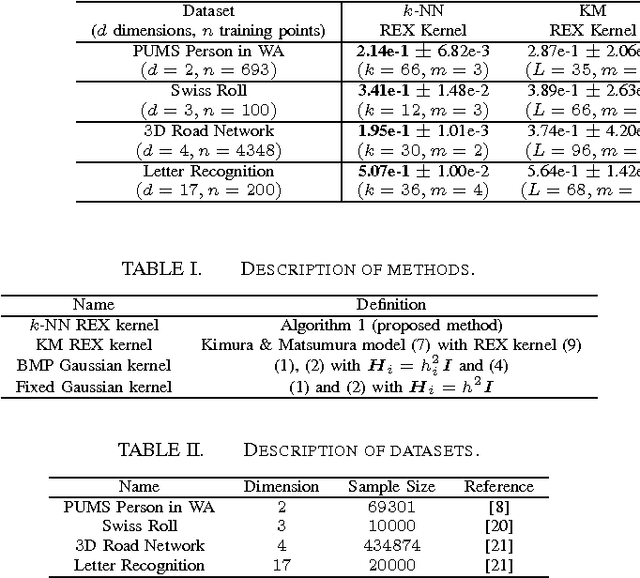
The recent development of multi-agent simulations brings about a need for population synthesis. It is a task of reconstructing the entire population from a sampling survey of limited size (1% or so), supplying the initial conditions from which simulations begin. This paper presents a new kernel density estimator for this task. Our method is an analogue of the classical Breiman-Meisel-Purcell estimator, but employs novel techniques that harness the huge degree of freedom which is required to model high-dimensional nonlinearly correlated datasets: the crossover kernel, the k-nearest neighbor restriction of the kernel construction set and the bagging of kernels. The performance as a statistical estimator is examined through real and synthetic datasets. We provide an "optimization-free" parameter selection rule for our method, a theory of how our method works and a computational cost analysis. To demonstrate the usefulness as a population synthesizer, our method is applied to a household synthesis task for an urban micro-simulator.