Simple Problems: The Simplicial Gluing Structure of Pareto Sets and Pareto Fronts
Paper and Code
Apr 18, 2017
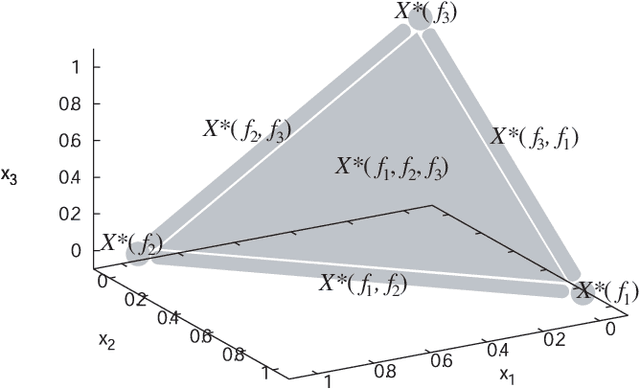


Quite a few studies on real-world applications of multi-objective optimization reported that their Pareto sets and Pareto fronts form a topological simplex. Such a class of problems was recently named the simple problems, and their Pareto set and Pareto front were observed to have a gluing structure similar to the faces of a simplex. This paper gives a theoretical justification for that observation by proving the gluing structure of the Pareto sets/fronts of subproblems of a simple problem. The simplicity of standard benchmark problems is studied.
* 10 pages, accepted at GECCO'17 as a poster paper (2 pages)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge