A Two-phase Framework with a Bézier Simplex-based Interpolation Method for Computationally Expensive Multi-objective Optimization

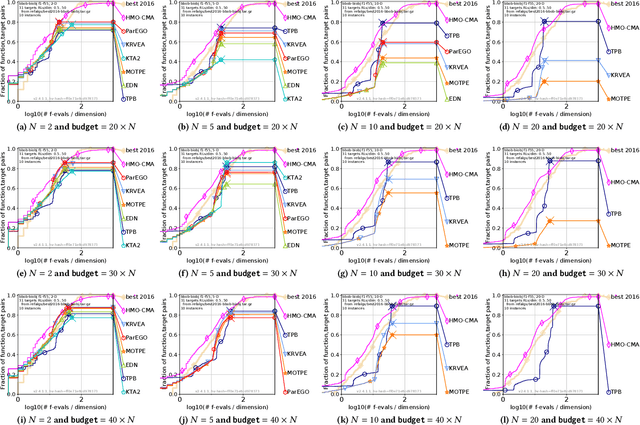
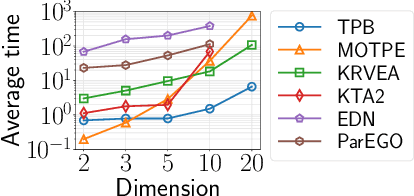
This paper proposes a two-phase framework with a B\'{e}zier simplex-based interpolation method (TPB) for computationally expensive multi-objective optimization. The first phase in TPB aims to approximate a few Pareto optimal solutions by optimizing a sequence of single-objective scalar problems. The first phase in TPB can fully exploit a state-of-the-art single-objective derivative-free optimizer. The second phase in TPB utilizes a B\'{e}zier simplex model to interpolate the solutions obtained in the first phase. The second phase in TPB fully exploits the fact that a B\'{e}zier simplex model can approximate the Pareto optimal solution set by exploiting its simplex structure when a given problem is simplicial. We investigate the performance of TPB on the 55 bi-objective BBOB problems. The results show that TPB performs significantly better than HMO-CMA-ES and some state-of-the-art meta-model-based optimizers.