Population Synthesis via k-Nearest Neighbor Crossover Kernel
Paper and Code
Aug 26, 2015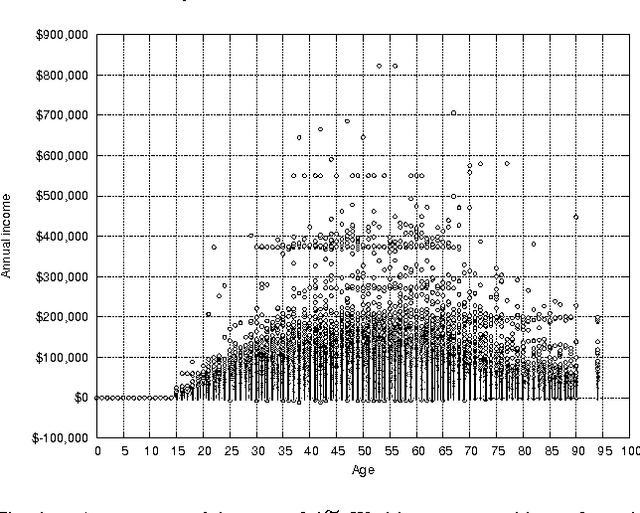
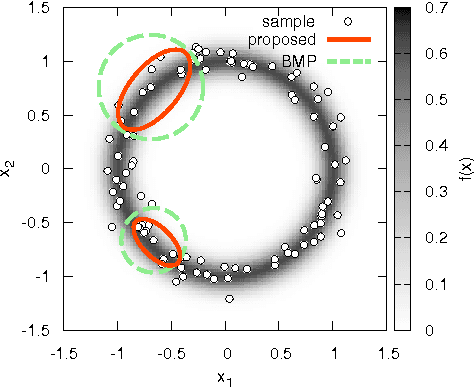
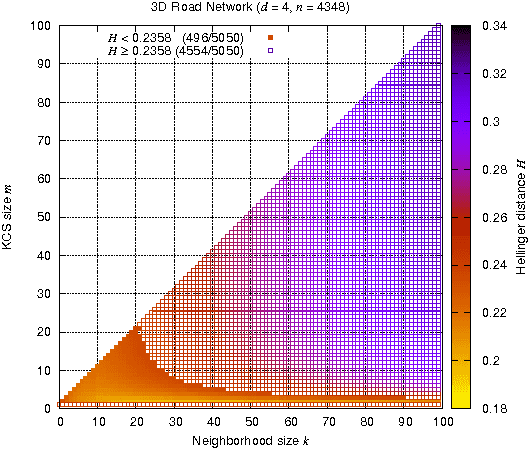
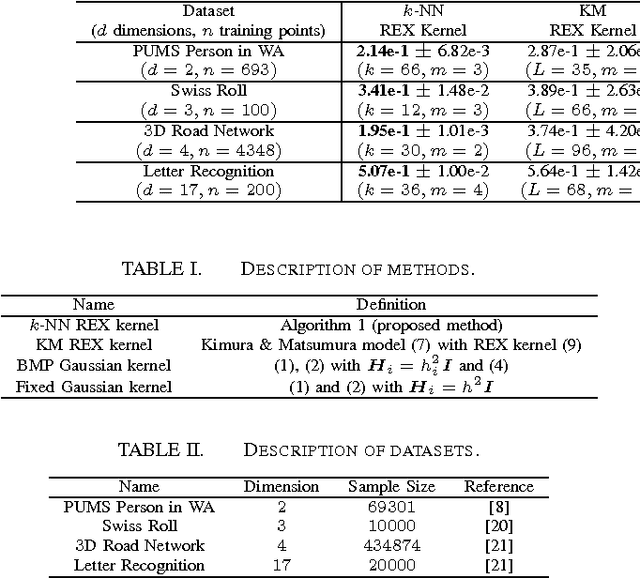
The recent development of multi-agent simulations brings about a need for population synthesis. It is a task of reconstructing the entire population from a sampling survey of limited size (1% or so), supplying the initial conditions from which simulations begin. This paper presents a new kernel density estimator for this task. Our method is an analogue of the classical Breiman-Meisel-Purcell estimator, but employs novel techniques that harness the huge degree of freedom which is required to model high-dimensional nonlinearly correlated datasets: the crossover kernel, the k-nearest neighbor restriction of the kernel construction set and the bagging of kernels. The performance as a statistical estimator is examined through real and synthetic datasets. We provide an "optimization-free" parameter selection rule for our method, a theory of how our method works and a computational cost analysis. To demonstrate the usefulness as a population synthesizer, our method is applied to a household synthesis task for an urban micro-simulator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge