Decomposition of Equivariant Maps via Invariant Maps: Application to Universal Approximation under Symmetry

In this paper, we develop a theory about the relationship between invariant and equivariant maps with regard to a group $G$. We then leverage this theory in the context of deep neural networks with group symmetries in order to obtain novel insight into their mechanisms. More precisely, we establish a one-to-one relationship between equivariant maps and certain invariant maps. This allows us to reduce arguments for equivariant maps to those for invariant maps and vice versa. As an application, we propose a construction of universal equivariant architectures built from universal invariant networks. We, in turn, explain how the universal architectures arising from our construction differ from standard equivariant architectures known to be universal. Furthermore, we explore the complexity, in terms of the number of free parameters, of our models, and discuss the relation between invariant and equivariant networks' complexity. Finally, we also give an approximation rate for G-equivariant deep neural networks with ReLU activation functions for finite group G.

Unification of Symmetries Inside Neural Networks: Transformer, Feedforward and Neural ODE

Understanding the inner workings of neural networks, including transformers, remains one of the most challenging puzzles in machine learning. This study introduces a novel approach by applying the principles of gauge symmetries, a key concept in physics, to neural network architectures. By regarding model functions as physical observables, we find that parametric redundancies of various machine learning models can be interpreted as gauge symmetries. We mathematically formulate the parametric redundancies in neural ODEs, and find that their gauge symmetries are given by spacetime diffeomorphisms, which play a fundamental role in Einstein's theory of gravity. Viewing neural ODEs as a continuum version of feedforward neural networks, we show that the parametric redundancies in feedforward neural networks are indeed lifted to diffeomorphisms in neural ODEs. We further extend our analysis to transformer models, finding natural correspondences with neural ODEs and their gauge symmetries. The concept of gauge symmetries sheds light on the complex behavior of deep learning models through physics and provides us with a unifying perspective for analyzing various machine learning architectures.

A Policy Gradient Primal-Dual Algorithm for Constrained MDPs with Uniform PAC Guarantees

We study a primal-dual reinforcement learning (RL) algorithm for the online constrained Markov decision processes (CMDP) problem, wherein the agent explores an optimal policy that maximizes return while satisfying constraints. Despite its widespread practical use, the existing theoretical literature on primal-dual RL algorithms for this problem only provides sublinear regret guarantees and fails to ensure convergence to optimal policies. In this paper, we introduce a novel policy gradient primal-dual algorithm with uniform probably approximate correctness (Uniform-PAC) guarantees, simultaneously ensuring convergence to optimal policies, sublinear regret, and polynomial sample complexity for any target accuracy. Notably, this represents the first Uniform-PAC algorithm for the online CMDP problem. In addition to the theoretical guarantees, we empirically demonstrate in a simple CMDP that our algorithm converges to optimal policies, while an existing algorithm exhibits oscillatory performance and constraint violation.

Integrating Large Language Models in Causal Discovery: A Statistical Causal Approach

In practical statistical causal discovery (SCD), embedding domain expert knowledge as constraints into the algorithm is widely accepted as significant for creating consistent meaningful causal models, despite the recognized challenges in systematic acquisition of the background knowledge. To overcome these challenges, this paper proposes a novel methodology for causal inference, in which SCD methods and knowledge based causal inference (KBCI) with a large language model (LLM) are synthesized through "statistical causal prompting (SCP)" for LLMs and prior knowledge augmentation for SCD. Experiments have revealed that GPT-4 can cause the output of the LLM-KBCI and the SCD result with prior knowledge from LLM-KBCI to approach the ground truth, and that the SCD result can be further improved, if GPT-4 undergoes SCP. Furthermore, it has been clarified that an LLM can improve SCD with its background knowledge, even if the LLM does not contain information on the dataset. The proposed approach can thus address challenges such as dataset biases and limitations, illustrating the potential of LLMs to improve data-driven causal inference across diverse scientific domains.

LPML: LLM-Prompting Markup Language for Mathematical Reasoning

In utilizing large language models (LLMs) for mathematical reasoning, addressing the errors in the reasoning and calculation present in the generated text by LLMs is a crucial challenge. In this paper, we propose a novel framework that integrates the Chain-of-Thought (CoT) method with an external tool (Python REPL). We discovered that by prompting LLMs to generate structured text in XML-like markup language, we could seamlessly integrate CoT and the external tool and control the undesired behaviors of LLMs. With our approach, LLMs can utilize Python computation to rectify errors within CoT. We applied our method to ChatGPT (GPT-3.5) to solve challenging mathematical problems and demonstrated that combining CoT and Python REPL through the markup language enhances the reasoning capability of LLMs. Our approach enables LLMs to write the markup language and perform advanced mathematical reasoning using only zero-shot prompting.

Bézier Flow: a Surface-wise Gradient Descent Method for Multi-objective Optimization

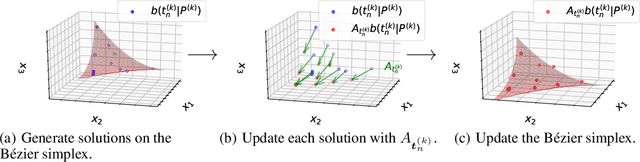
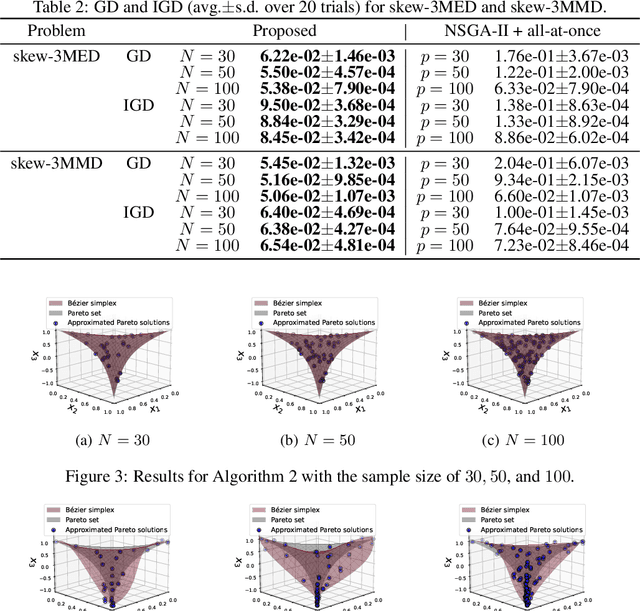
In this paper, we propose a strategy to construct a multi-objective optimization algorithm from a single-objective optimization algorithm by using the B\'ezier simplex model. Also, we extend the stability of optimization algorithms in the sense of Probability Approximately Correct (PAC) learning and define the PAC stability. We prove that it leads to an upper bound on the generalization with high probability. Furthermore, we show that multi-objective optimization algorithms derived from a gradient descent-based single-objective optimization algorithm are PAC stable. We conducted numerical experiments and demonstrated that our method achieved lower generalization errors than the existing multi-objective optimization algorithm.

Equivariant and Invariant Reynolds Networks

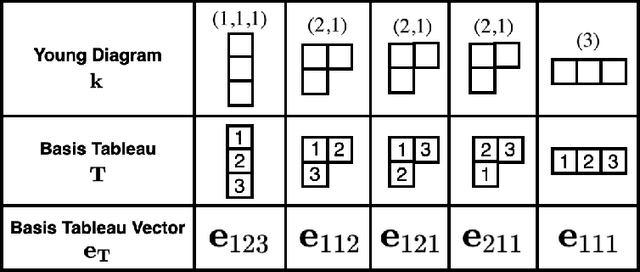
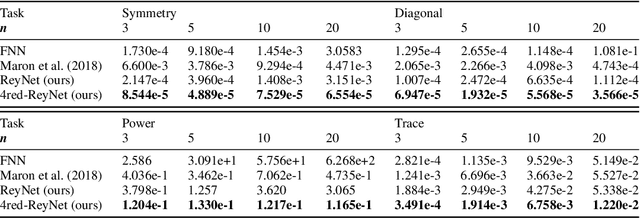
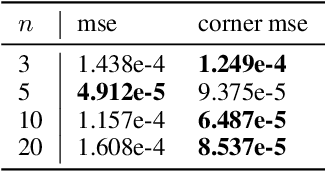
Invariant and equivariant networks are useful in learning data with symmetry, including images, sets, point clouds, and graphs. In this paper, we consider invariant and equivariant networks for symmetries of finite groups. Invariant and equivariant networks have been constructed by various researchers using Reynolds operators. However, Reynolds operators are computationally expensive when the order of the group is large because they use the sum over the whole group, which poses an implementation difficulty. To overcome this difficulty, we consider representing the Reynolds operator as a sum over a subset instead of a sum over the whole group. We call such a subset a Reynolds design, and an operator defined by a sum over a Reynolds design a reductive Reynolds operator. For example, in the case of a graph with $n$ nodes, the computational complexity of the reductive Reynolds operator is reduced to $O(n^2)$, while the computational complexity of the Reynolds operator is $O(n!)$. We construct learning models based on the reductive Reynolds operator called equivariant and invariant Reynolds networks (ReyNets) and prove that they have universal approximation property. Reynolds designs for equivariant ReyNets are derived from combinatorial observations with Young diagrams, while Reynolds designs for invariant ReyNets are derived from invariants called Reynolds dimensions defined on the set of invariant polynomials. Numerical experiments show that the performance of our models is comparable to state-of-the-art methods.

Approximate Bayesian Computation of Bézier Simplices

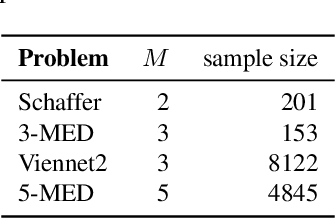
B\'ezier simplex fitting algorithms have been recently proposed to approximate the Pareto set/front of multi-objective continuous optimization problems. These new methods have shown to be successful at approximating various shapes of Pareto sets/fronts when sample points exactly lie on the Pareto set/front. However, if the sample points scatter away from the Pareto set/front, those methods often likely suffer from over-fitting. To overcome this issue, in this paper, we extend the B\'ezier simplex model to a probabilistic one and propose a new learning algorithm of it, which falls into the framework of approximate Bayesian computation (ABC) based on the Wasserstein distance. We also study the convergence property of the Wasserstein ABC algorithm. An extensive experimental evaluation on publicly available problem instances shows that the new algorithm converges on a finite sample. Moreover, it outperforms the deterministic fitting methods on noisy instances.

Group Equivariant Conditional Neural Processes

We present the group equivariant conditional neural process (EquivCNP), a meta-learning method with permutation invariance in a data set as in conventional conditional neural processes (CNPs), and it also has transformation equivariance in data space. Incorporating group equivariance, such as rotation and scaling equivariance, provides a way to consider the symmetry of real-world data. We give a decomposition theorem for permutation-invariant and group-equivariant maps, which leads us to construct EquivCNPs with an infinite-dimensional latent space to handle group symmetries. In this paper, we build architecture using Lie group convolutional layers for practical implementation. We show that EquivCNP with translation equivariance achieves comparable performance to conventional CNPs in a 1D regression task. Moreover, we demonstrate that incorporating an appropriate Lie group equivariance, EquivCNP is capable of zero-shot generalization for an image-completion task by selecting an appropriate Lie group equivariance.

Universal Approximation Theorem for Equivariant Maps by Group CNNs

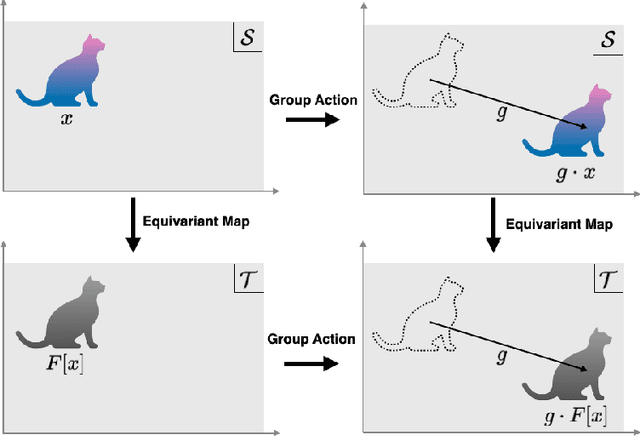
Group symmetry is inherent in a wide variety of data distributions. Data processing that preserves symmetry is described as an equivariant map and often effective in achieving high performance. Convolutional neural networks (CNNs) have been known as models with equivariance and shown to approximate equivariant maps for some specific groups. However, universal approximation theorems for CNNs have been separately derived with individual techniques according to each group and setting. This paper provides a unified method to obtain universal approximation theorems for equivariant maps by CNNs in various settings. As its significant advantage, we can handle non-linear equivariant maps between infinite-dimensional spaces for non-compact groups.