Universal Approximation Theorem for Equivariant Maps by Group CNNs
Paper and Code
Dec 27, 2020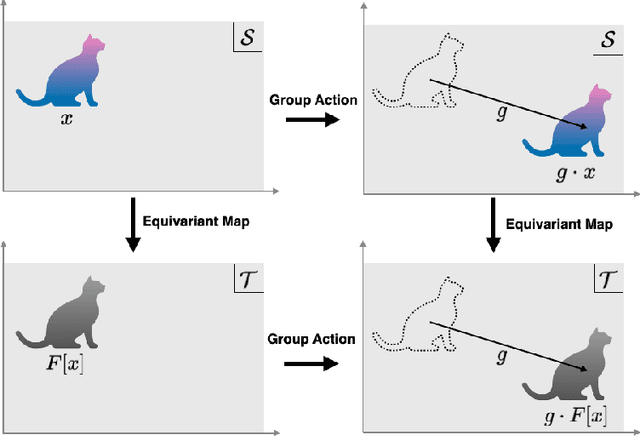
Group symmetry is inherent in a wide variety of data distributions. Data processing that preserves symmetry is described as an equivariant map and often effective in achieving high performance. Convolutional neural networks (CNNs) have been known as models with equivariance and shown to approximate equivariant maps for some specific groups. However, universal approximation theorems for CNNs have been separately derived with individual techniques according to each group and setting. This paper provides a unified method to obtain universal approximation theorems for equivariant maps by CNNs in various settings. As its significant advantage, we can handle non-linear equivariant maps between infinite-dimensional spaces for non-compact groups.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge