A Dataset for Evaluating LLM-based Evaluation Functions for Research Question Extraction Task

The progress in text summarization techniques has been remarkable. However the task of accurately extracting and summarizing necessary information from highly specialized documents such as research papers has not been sufficiently investigated. We are focusing on the task of extracting research questions (RQ) from research papers and construct a new dataset consisting of machine learning papers, RQ extracted from these papers by GPT-4, and human evaluations of the extracted RQ from multiple perspectives. Using this dataset, we systematically compared recently proposed LLM-based evaluation functions for summarizations, and found that none of the functions showed sufficiently high correlations with human evaluations. We expect our dataset provides a foundation for further research on developing better evaluation functions tailored to the RQ extraction task, and contribute to enhance the performance of the task. The dataset is available at https://github.com/auto-res/PaperRQ-HumanAnno-Dataset.

Near-Optimal Policy Identification in Robust Constrained Markov Decision Processes via Epigraph Form

Designing a safe policy for uncertain environments is crucial in real-world control applications. However, this challenge remains inadequately addressed within the Markov decision process (MDP) framework. This paper presents the first algorithm capable of identifying a near-optimal policy in a robust constrained MDP (RCMDP), where an optimal policy minimizes cumulative cost while satisfying constraints in the worst-case scenario across a set of environments. We first prove that the conventional Lagrangian max-min formulation with policy gradient methods can become trapped in suboptimal solutions by encountering a sum of conflicting gradients from the objective and constraint functions during its inner minimization problem. To address this, we leverage the epigraph form of the RCMDP problem, which resolves the conflict by selecting a single gradient from either the objective or the constraints. Building on the epigraph form, we propose a binary search algorithm with a policy gradient subroutine and prove that it identifies an $\varepsilon$-optimal policy in an RCMDP with $\tilde{\mathcal{O}}(\varepsilon^{-4})$ policy evaluations.

A Policy Gradient Primal-Dual Algorithm for Constrained MDPs with Uniform PAC Guarantees

We study a primal-dual reinforcement learning (RL) algorithm for the online constrained Markov decision processes (CMDP) problem, wherein the agent explores an optimal policy that maximizes return while satisfying constraints. Despite its widespread practical use, the existing theoretical literature on primal-dual RL algorithms for this problem only provides sublinear regret guarantees and fails to ensure convergence to optimal policies. In this paper, we introduce a novel policy gradient primal-dual algorithm with uniform probably approximate correctness (Uniform-PAC) guarantees, simultaneously ensuring convergence to optimal policies, sublinear regret, and polynomial sample complexity for any target accuracy. Notably, this represents the first Uniform-PAC algorithm for the online CMDP problem. In addition to the theoretical guarantees, we empirically demonstrate in a simple CMDP that our algorithm converges to optimal policies, while an existing algorithm exhibits oscillatory performance and constraint violation.

Towards Autonomous Hypothesis Verification via Language Models with Minimal Guidance

Research automation efforts usually employ AI as a tool to automate specific tasks within the research process. To create an AI that truly conduct research themselves, it must independently generate hypotheses, design verification plans, and execute verification. Therefore, we investigated if an AI itself could autonomously generate and verify hypothesis for a toy machine learning research problem. We prompted GPT-4 to generate hypotheses and Python code for hypothesis verification with limited methodological guidance. Our findings suggest that, in some instances, GPT-4 can autonomously generate and validate hypotheses without detailed guidance. While this is a promising result, we also found that none of the verifications were flawless, and there remain significant challenges in achieving autonomous, human-level research using only generic instructions. These findings underscore the need for continued exploration to develop a general and autonomous AI researcher.

LPML: LLM-Prompting Markup Language for Mathematical Reasoning

In utilizing large language models (LLMs) for mathematical reasoning, addressing the errors in the reasoning and calculation present in the generated text by LLMs is a crucial challenge. In this paper, we propose a novel framework that integrates the Chain-of-Thought (CoT) method with an external tool (Python REPL). We discovered that by prompting LLMs to generate structured text in XML-like markup language, we could seamlessly integrate CoT and the external tool and control the undesired behaviors of LLMs. With our approach, LLMs can utilize Python computation to rectify errors within CoT. We applied our method to ChatGPT (GPT-3.5) to solve challenging mathematical problems and demonstrated that combining CoT and Python REPL through the markup language enhances the reasoning capability of LLMs. Our approach enables LLMs to write the markup language and perform advanced mathematical reasoning using only zero-shot prompting.

Regularization and Variance-Weighted Regression Achieves Minimax Optimality in Linear MDPs: Theory and Practice

Mirror descent value iteration (MDVI), an abstraction of Kullback-Leibler (KL) and entropy-regularized reinforcement learning (RL), has served as the basis for recent high-performing practical RL algorithms. However, despite the use of function approximation in practice, the theoretical understanding of MDVI has been limited to tabular Markov decision processes (MDPs). We study MDVI with linear function approximation through its sample complexity required to identify an $\varepsilon$-optimal policy with probability $1-\delta$ under the settings of an infinite-horizon linear MDP, generative model, and G-optimal design. We demonstrate that least-squares regression weighted by the variance of an estimated optimal value function of the next state is crucial to achieving minimax optimality. Based on this observation, we present Variance-Weighted Least-Squares MDVI (VWLS-MDVI), the first theoretical algorithm that achieves nearly minimax optimal sample complexity for infinite-horizon linear MDPs. Furthermore, we propose a practical VWLS algorithm for value-based deep RL, Deep Variance Weighting (DVW). Our experiments demonstrate that DVW improves the performance of popular value-based deep RL algorithms on a set of MinAtar benchmarks.

Langevin Autoencoders for Learning Deep Latent Variable Models

Markov chain Monte Carlo (MCMC), such as Langevin dynamics, is valid for approximating intractable distributions. However, its usage is limited in the context of deep latent variable models owing to costly datapoint-wise sampling iterations and slow convergence. This paper proposes the amortized Langevin dynamics (ALD), wherein datapoint-wise MCMC iterations are entirely replaced with updates of an encoder that maps observations into latent variables. This amortization enables efficient posterior sampling without datapoint-wise iterations. Despite its efficiency, we prove that ALD is valid as an MCMC algorithm, whose Markov chain has the target posterior as a stationary distribution under mild assumptions. Based on the ALD, we also present a new deep latent variable model named the Langevin autoencoder (LAE). Interestingly, the LAE can be implemented by slightly modifying the traditional autoencoder. Using multiple synthetic datasets, we first validate that ALD can properly obtain samples from target posteriors. We also evaluate the LAE on the image generation task, and show that our LAE can outperform existing methods based on variational inference, such as the variational autoencoder, and other MCMC-based methods in terms of the test likelihood.

Equivariant and Invariant Reynolds Networks

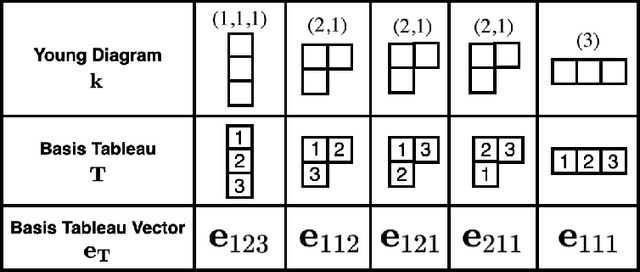
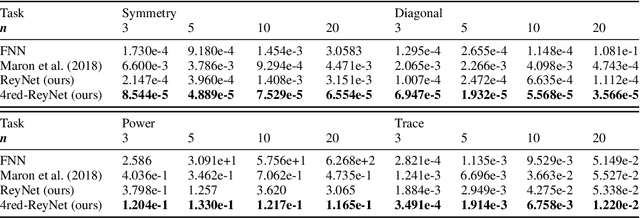
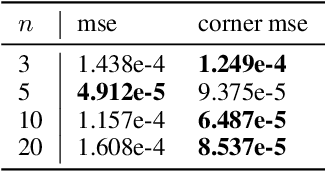
Invariant and equivariant networks are useful in learning data with symmetry, including images, sets, point clouds, and graphs. In this paper, we consider invariant and equivariant networks for symmetries of finite groups. Invariant and equivariant networks have been constructed by various researchers using Reynolds operators. However, Reynolds operators are computationally expensive when the order of the group is large because they use the sum over the whole group, which poses an implementation difficulty. To overcome this difficulty, we consider representing the Reynolds operator as a sum over a subset instead of a sum over the whole group. We call such a subset a Reynolds design, and an operator defined by a sum over a Reynolds design a reductive Reynolds operator. For example, in the case of a graph with $n$ nodes, the computational complexity of the reductive Reynolds operator is reduced to $O(n^2)$, while the computational complexity of the Reynolds operator is $O(n!)$. We construct learning models based on the reductive Reynolds operator called equivariant and invariant Reynolds networks (ReyNets) and prove that they have universal approximation property. Reynolds designs for equivariant ReyNets are derived from combinatorial observations with Young diagrams, while Reynolds designs for invariant ReyNets are derived from invariants called Reynolds dimensions defined on the set of invariant polynomials. Numerical experiments show that the performance of our models is comparable to state-of-the-art methods.

Group Equivariant Conditional Neural Processes

We present the group equivariant conditional neural process (EquivCNP), a meta-learning method with permutation invariance in a data set as in conventional conditional neural processes (CNPs), and it also has transformation equivariance in data space. Incorporating group equivariance, such as rotation and scaling equivariance, provides a way to consider the symmetry of real-world data. We give a decomposition theorem for permutation-invariant and group-equivariant maps, which leads us to construct EquivCNPs with an infinite-dimensional latent space to handle group symmetries. In this paper, we build architecture using Lie group convolutional layers for practical implementation. We show that EquivCNP with translation equivariance achieves comparable performance to conventional CNPs in a 1D regression task. Moreover, we demonstrate that incorporating an appropriate Lie group equivariance, EquivCNP is capable of zero-shot generalization for an image-completion task by selecting an appropriate Lie group equivariance.

Universal Approximation Theorem for Equivariant Maps by Group CNNs

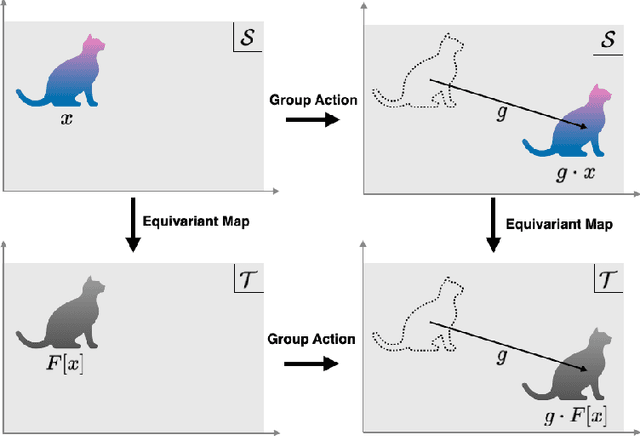
Group symmetry is inherent in a wide variety of data distributions. Data processing that preserves symmetry is described as an equivariant map and often effective in achieving high performance. Convolutional neural networks (CNNs) have been known as models with equivariance and shown to approximate equivariant maps for some specific groups. However, universal approximation theorems for CNNs have been separately derived with individual techniques according to each group and setting. This paper provides a unified method to obtain universal approximation theorems for equivariant maps by CNNs in various settings. As its significant advantage, we can handle non-linear equivariant maps between infinite-dimensional spaces for non-compact groups.