A Batch Sequential Halving Algorithm without Performance Degradation

In this paper, we investigate the problem of pure exploration in the context of multi-armed bandits, with a specific focus on scenarios where arms are pulled in fixed-size batches. Batching has been shown to enhance computational efficiency, but it can potentially lead to a degradation compared to the original sequential algorithm's performance due to delayed feedback and reduced adaptability. We introduce a simple batch version of the Sequential Halving (SH) algorithm (Karnin et al., 2013) and provide theoretical evidence that batching does not degrade the performance of the original algorithm under practical conditions. Furthermore, we empirically validate our claim through experiments, demonstrating the robust nature of the SH algorithm in fixed-size batch settings.

Leveraging Domain-Unlabeled Data in Offline Reinforcement Learning across Two Domains

In this paper, we investigate an offline reinforcement learning (RL) problem where datasets are collected from two domains. In this scenario, having datasets with domain labels facilitates efficient policy training. However, in practice, the task of assigning domain labels can be resource-intensive or infeasible at a large scale, leading to a prevalence of domain-unlabeled data. To formalize this challenge, we introduce a novel offline RL problem setting named Positive-Unlabeled Offline RL (PUORL), which incorporates domain-unlabeled data. To address PUORL, we develop an offline RL algorithm utilizing positive-unlabeled learning to predict the domain labels of domain-unlabeled data, enabling the integration of this data into policy training. Our experiments show the effectiveness of our method in accurately identifying domains and learning policies that outperform baselines in the PUORL setting, highlighting its capability to leverage domain-unlabeled data effectively.

A Policy Gradient Primal-Dual Algorithm for Constrained MDPs with Uniform PAC Guarantees

We study a primal-dual reinforcement learning (RL) algorithm for the online constrained Markov decision processes (CMDP) problem, wherein the agent explores an optimal policy that maximizes return while satisfying constraints. Despite its widespread practical use, the existing theoretical literature on primal-dual RL algorithms for this problem only provides sublinear regret guarantees and fails to ensure convergence to optimal policies. In this paper, we introduce a novel policy gradient primal-dual algorithm with uniform probably approximate correctness (Uniform-PAC) guarantees, simultaneously ensuring convergence to optimal policies, sublinear regret, and polynomial sample complexity for any target accuracy. Notably, this represents the first Uniform-PAC algorithm for the online CMDP problem. In addition to the theoretical guarantees, we empirically demonstrate in a simple CMDP that our algorithm converges to optimal policies, while an existing algorithm exhibits oscillatory performance and constraint violation.

End-to-End Policy Gradient Method for POMDPs and Explainable Agents

Real-world decision-making problems are often partially observable, and many can be formulated as a Partially Observable Markov Decision Process (POMDP). When we apply reinforcement learning (RL) algorithms to the POMDP, reasonable estimation of the hidden states can help solve the problems. Furthermore, explainable decision-making is preferable, considering their application to real-world tasks such as autonomous driving cars. We proposed an RL algorithm that estimates the hidden states by end-to-end training, and visualize the estimation as a state-transition graph. Experimental results demonstrated that the proposed algorithm can solve simple POMDP problems and that the visualization makes the agent's behavior interpretable to humans.

Pgx: Hardware-accelerated parallel game simulation for reinforcement learning

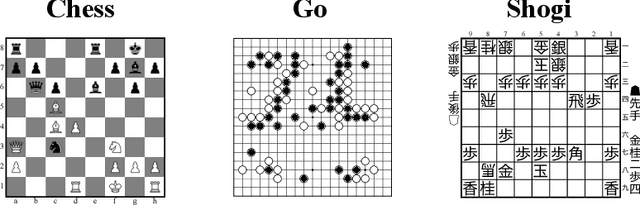
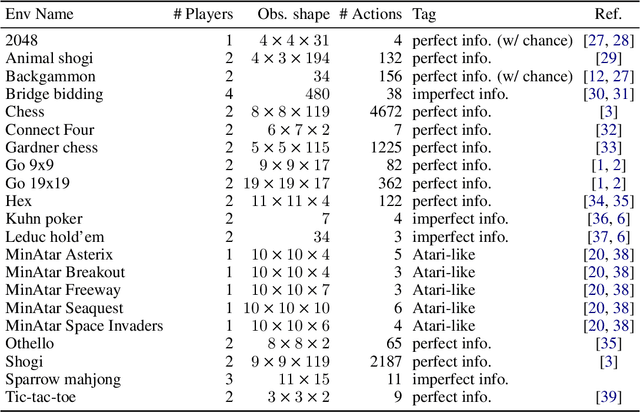
We propose Pgx, a collection of board game simulators written in JAX. Thanks to auto-vectorization and Just-In-Time compilation of JAX, Pgx scales easily to thousands of parallel execution on GPU/TPU accelerators. We found that the simulation of Pgx on a single A100 GPU is 10x faster than that of existing reinforcement learning libraries. Pgx implements games considered vital benchmarks in artificial intelligence research, such as Backgammon, Shogi, and Go. Pgx is available at https://github.com/sotetsuk/pgx.