Near-Optimal Policy Identification in Robust Constrained Markov Decision Processes via Epigraph Form

Designing a safe policy for uncertain environments is crucial in real-world control applications. However, this challenge remains inadequately addressed within the Markov decision process (MDP) framework. This paper presents the first algorithm capable of identifying a near-optimal policy in a robust constrained MDP (RCMDP), where an optimal policy minimizes cumulative cost while satisfying constraints in the worst-case scenario across a set of environments. We first prove that the conventional Lagrangian max-min formulation with policy gradient methods can become trapped in suboptimal solutions by encountering a sum of conflicting gradients from the objective and constraint functions during its inner minimization problem. To address this, we leverage the epigraph form of the RCMDP problem, which resolves the conflict by selecting a single gradient from either the objective or the constraints. Building on the epigraph form, we propose a binary search algorithm with a policy gradient subroutine and prove that it identifies an $\varepsilon$-optimal policy in an RCMDP with $\tilde{\mathcal{O}}(\varepsilon^{-4})$ policy evaluations.

A unified view of likelihood ratio and reparameterization gradients

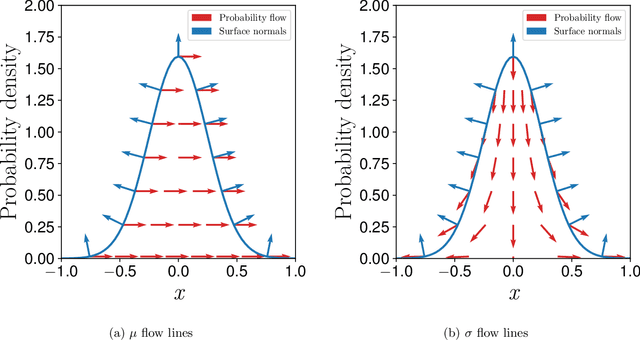
Reparameterization (RP) and likelihood ratio (LR) gradient estimators are used to estimate gradients of expectations throughout machine learning and reinforcement learning; however, they are usually explained as simple mathematical tricks, with no insight into their nature. We use a first principles approach to explain that LR and RP are alternative methods of keeping track of the movement of probability mass, and the two are connected via the divergence theorem. Moreover, we show that the space of all possible estimators combining LR and RP can be completely parameterized by a flow field $u(x)$ and an importance sampling distribution $q(x)$. We prove that there cannot exist a single-sample estimator of this type outside our characterized space, thus, clarifying where we should be searching for better Monte Carlo gradient estimators.

A unified view of likelihood ratio and reparameterization gradients and an optimal importance sampling scheme

Reparameterization (RP) and likelihood ratio (LR) gradient estimators are used throughout machine and reinforcement learning; however, they are usually explained as simple mathematical tricks without providing any insight into their nature. We use a first principles approach to explain LR and RP, and show a connection between the two via the divergence theorem. The theory motivated us to derive optimal importance sampling schemes to reduce LR gradient variance. Our newly derived distributions have analytic probability densities and can be directly sampled from. The improvement for Gaussian target distributions was modest, but for other distributions such as a Beta distribution, our method could lead to arbitrarily large improvements, and was crucial to obtain competitive performance in evolution strategies experiments.

Total stochastic gradient algorithms and applications in reinforcement learning

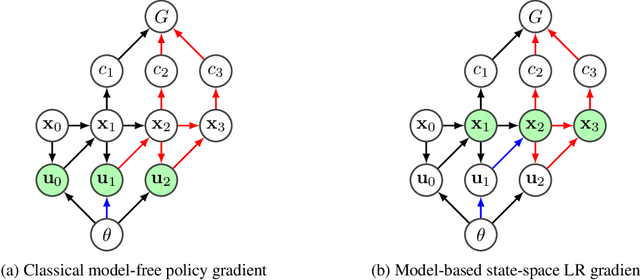
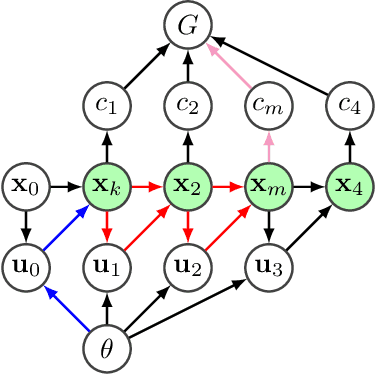
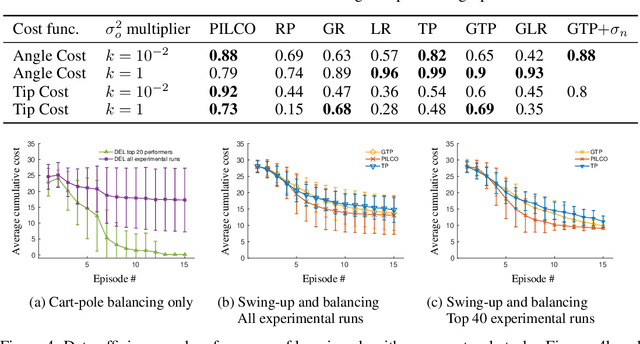
Backpropagation and the chain rule of derivatives have been prominent; however, the total derivative rule has not enjoyed the same amount of attention. In this work we show how the total derivative rule leads to an intuitive visual framework for creating gradient estimators on graphical models. In particular, previous "policy gradient theorems" are easily derived. We derive new gradient estimators based on density estimation, as well as a likelihood ratio gradient, which "jumps" to an intermediate node, not directly to the objective function. We evaluate our methods on model-based policy gradient algorithms, achieve good performance, and present evidence towards demystifying the success of the popular PILCO algorithm.

PIPPS: Flexible Model-Based Policy Search Robust to the Curse of Chaos

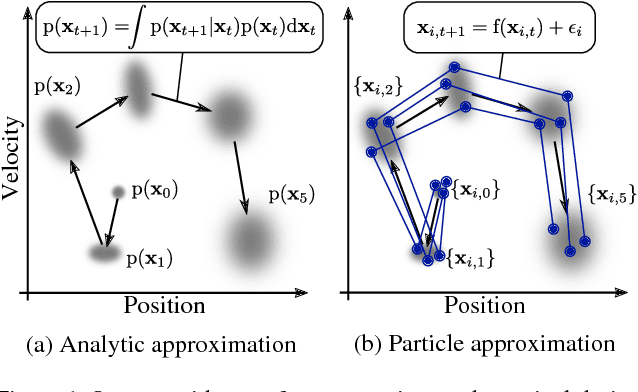
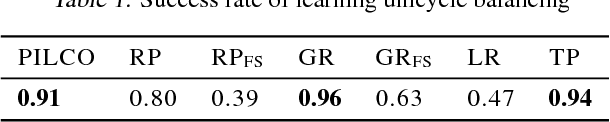
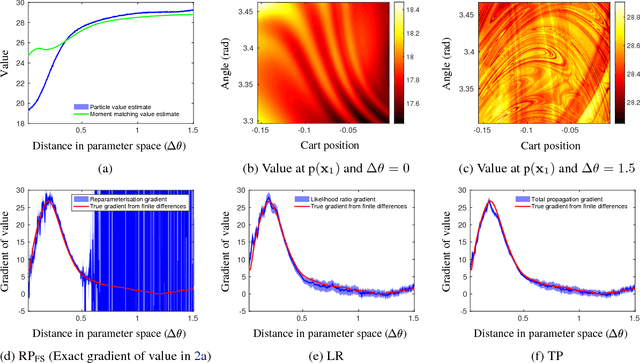
Previously, the exploding gradient problem has been explained to be central in deep learning and model-based reinforcement learning, because it causes numerical issues and instability in optimization. Our experiments in model-based reinforcement learning imply that the problem is not just a numerical issue, but it may be caused by a fundamental chaos-like nature of long chains of nonlinear computations. Not only do the magnitudes of the gradients become large, the direction of the gradients becomes essentially random. We show that reparameterization gradients suffer from the problem, while likelihood ratio gradients are robust. Using our insights, we develop a model-based policy search framework, Probabilistic Inference for Particle-Based Policy Search (PIPPS), which is easily extensible, and allows for almost arbitrary models and policies, while simultaneously matching the performance of previous data-efficient learning algorithms. Finally, we invent the total propagation algorithm, which efficiently computes a union over all pathwise derivative depths during a single backwards pass, automatically giving greater weight to estimators with lower variance, sometimes improving over reparameterization gradients by $10^6$ times.