Equivariant and Invariant Reynolds Networks
Paper and Code
Oct 15, 2021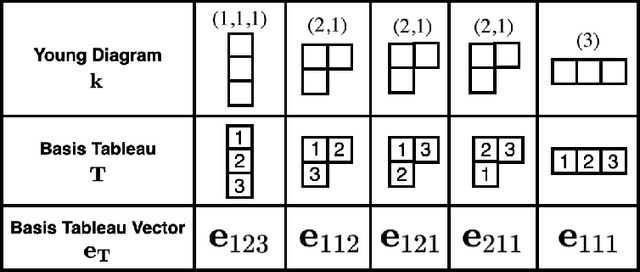
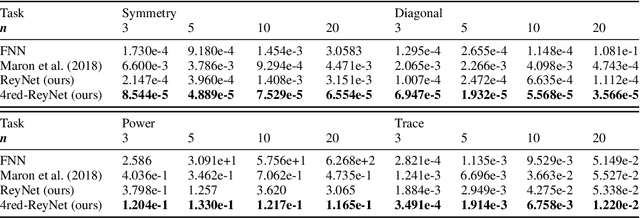

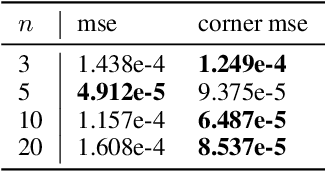
Invariant and equivariant networks are useful in learning data with symmetry, including images, sets, point clouds, and graphs. In this paper, we consider invariant and equivariant networks for symmetries of finite groups. Invariant and equivariant networks have been constructed by various researchers using Reynolds operators. However, Reynolds operators are computationally expensive when the order of the group is large because they use the sum over the whole group, which poses an implementation difficulty. To overcome this difficulty, we consider representing the Reynolds operator as a sum over a subset instead of a sum over the whole group. We call such a subset a Reynolds design, and an operator defined by a sum over a Reynolds design a reductive Reynolds operator. For example, in the case of a graph with $n$ nodes, the computational complexity of the reductive Reynolds operator is reduced to $O(n^2)$, while the computational complexity of the Reynolds operator is $O(n!)$. We construct learning models based on the reductive Reynolds operator called equivariant and invariant Reynolds networks (ReyNets) and prove that they have universal approximation property. Reynolds designs for equivariant ReyNets are derived from combinatorial observations with Young diagrams, while Reynolds designs for invariant ReyNets are derived from invariants called Reynolds dimensions defined on the set of invariant polynomials. Numerical experiments show that the performance of our models is comparable to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge