Machine-learning emergent spacetime from linear response in future tabletop quantum gravity experiments

We introduce a novel interpretable Neural Network (NN) model designed to perform precision bulk reconstruction under the AdS/CFT correspondence. According to the correspondence, a specific condensed matter system on a ring is holographically equivalent to a gravitational system on a bulk disk, through which tabletop quantum gravity experiments may be possible as reported in arXiv:2211.13863. The purpose of this paper is to reconstruct a higher-dimensional gravity metric from the condensed matter system data via machine learning using the NN. Our machine reads spatially and temporarily inhomogeneous linear response data of the condensed matter system, and incorporates a novel layer that implements the Runge-Kutta method to achieve better numerical control. We confirm that our machine can let a higher-dimensional gravity metric be automatically emergent as its interpretable weights, using a linear response of the condensed matter system as data, through supervised machine learning. The developed method could serve as a foundation for generic bulk reconstruction, i.e., a practical solution to the AdS/CFT correspondence, and would be implemented in future tabletop quantum gravity experiments.

Comparative Study of Neural Network Methods for Solving Topological Solitons

Topological solitons, which are stable, localized solutions of nonlinear differential equations, are crucial in various fields of physics and mathematics, including particle physics and cosmology. However, solving these solitons presents significant challenges due to the complexity of the underlying equations and the computational resources required for accurate solutions. To address this, we have developed a novel method using neural network (NN) to efficiently solve solitons. A similar NN approach is Physics-Informed Neural Networks (PINN). In a comparative analysis between our method and PINN, we find that our method achieves shorter computation times while maintaining the same level of accuracy. This advancement in computational efficiency not only overcomes current limitations but also opens new avenues for studying topological solitons and their dynamical behavior.

Neural network representation of quantum systems

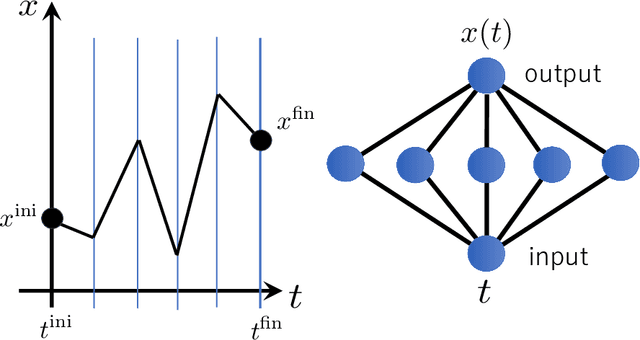
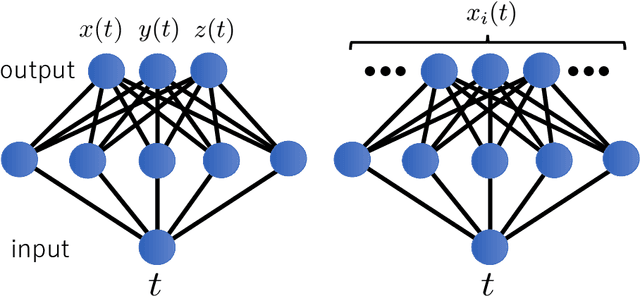
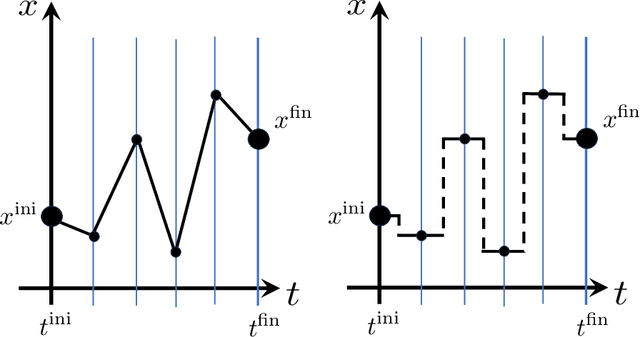
It has been proposed that random wide neural networks near Gaussian process are quantum field theories around Gaussian fixed points. In this paper, we provide a novel map with which a wide class of quantum mechanical systems can be cast into the form of a neural network with a statistical summation over network parameters. Our simple idea is to use the universal approximation theorem of neural networks to generate arbitrary paths in the Feynman's path integral. The map can be applied to interacting quantum systems / field theories, even away from the Gaussian limit. Our findings bring machine learning closer to the quantum world.

Unification of Symmetries Inside Neural Networks: Transformer, Feedforward and Neural ODE

Understanding the inner workings of neural networks, including transformers, remains one of the most challenging puzzles in machine learning. This study introduces a novel approach by applying the principles of gauge symmetries, a key concept in physics, to neural network architectures. By regarding model functions as physical observables, we find that parametric redundancies of various machine learning models can be interpreted as gauge symmetries. We mathematically formulate the parametric redundancies in neural ODEs, and find that their gauge symmetries are given by spacetime diffeomorphisms, which play a fundamental role in Einstein's theory of gravity. Viewing neural ODEs as a continuum version of feedforward neural networks, we show that the parametric redundancies in feedforward neural networks are indeed lifted to diffeomorphisms in neural ODEs. We further extend our analysis to transformer models, finding natural correspondences with neural ODEs and their gauge symmetries. The concept of gauge symmetries sheds light on the complex behavior of deep learning models through physics and provides us with a unifying perspective for analyzing various machine learning architectures.

Neural Polytopes

We find that simple neural networks with ReLU activation generate polytopes as an approximation of a unit sphere in various dimensions. The species of polytopes are regulated by the network architecture, such as the number of units and layers. For a variety of activation functions, generalization of polytopes is obtained, which we call neural polytopes. They are a smooth analogue of polytopes, exhibiting geometric duality. This finding initiates research of generative discrete geometry to approximate surfaces by machine learning.