Data-driven discovery of self-similarity using neural networks

Finding self-similarity is a key step for understanding the governing law behind complex physical phenomena. Traditional methods for identifying self-similarity often rely on specific models, which can introduce significant bias. In this paper, we present a novel neural network-based approach that discovers self-similarity directly from observed data, without presupposing any models. The presence of self-similar solutions in a physical problem signals that the governing law contains a function whose arguments are given by power-law monomials of physical parameters, which are characterized by power-law exponents. The basic idea is to enforce such particular forms structurally in a neural network in a parametrized way. We train the neural network model using the observed data, and when the training is successful, we can extract the power exponents that characterize scale-transformation symmetries of the physical problem. We demonstrate the effectiveness of our method with both synthetic and experimental data, validating its potential as a robust, model-independent tool for exploring self-similarity in complex systems.

Neural network representation of quantum systems

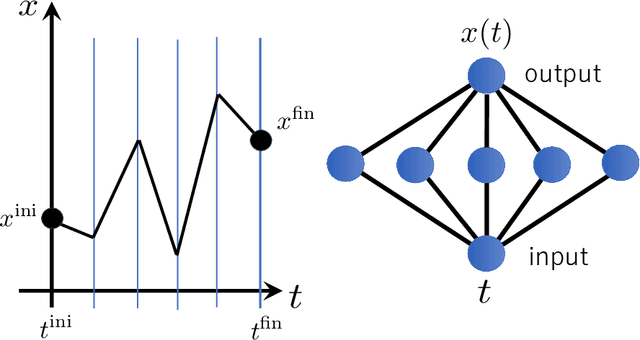
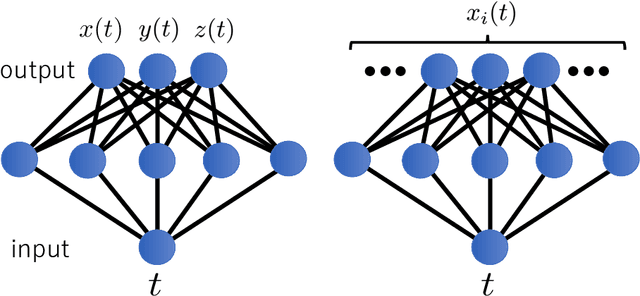
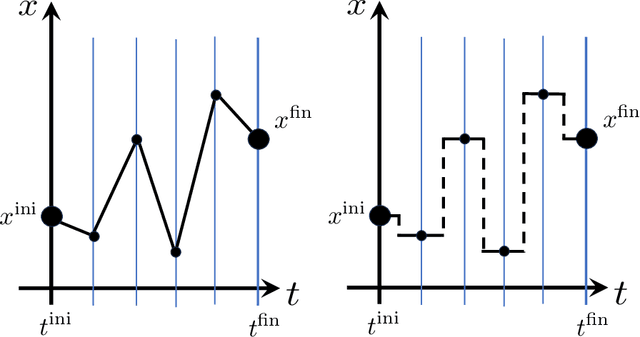
It has been proposed that random wide neural networks near Gaussian process are quantum field theories around Gaussian fixed points. In this paper, we provide a novel map with which a wide class of quantum mechanical systems can be cast into the form of a neural network with a statistical summation over network parameters. Our simple idea is to use the universal approximation theorem of neural networks to generate arbitrary paths in the Feynman's path integral. The map can be applied to interacting quantum systems / field theories, even away from the Gaussian limit. Our findings bring machine learning closer to the quantum world.

Understanding Diffusion Models by Feynman's Path Integral

Score-based diffusion models have proven effective in image generation and have gained widespread usage; however, the underlying factors contributing to the performance disparity between stochastic and deterministic (i.e., the probability flow ODEs) sampling schemes remain unclear. We introduce a novel formulation of diffusion models using Feynman's path integral, which is a formulation originally developed for quantum physics. We find this formulation providing comprehensive descriptions of score-based generative models, and demonstrate the derivation of backward stochastic differential equations and loss functions.The formulation accommodates an interpolating parameter connecting stochastic and deterministic sampling schemes, and we identify this parameter as a counterpart of Planck's constant in quantum physics. This analogy enables us to apply the Wentzel-Kramers-Brillouin (WKB) expansion, a well-established technique in quantum physics, for evaluating the negative log-likelihood to assess the performance disparity between stochastic and deterministic sampling schemes.

Unification of Symmetries Inside Neural Networks: Transformer, Feedforward and Neural ODE

Understanding the inner workings of neural networks, including transformers, remains one of the most challenging puzzles in machine learning. This study introduces a novel approach by applying the principles of gauge symmetries, a key concept in physics, to neural network architectures. By regarding model functions as physical observables, we find that parametric redundancies of various machine learning models can be interpreted as gauge symmetries. We mathematically formulate the parametric redundancies in neural ODEs, and find that their gauge symmetries are given by spacetime diffeomorphisms, which play a fundamental role in Einstein's theory of gravity. Viewing neural ODEs as a continuum version of feedforward neural networks, we show that the parametric redundancies in feedforward neural networks are indeed lifted to diffeomorphisms in neural ODEs. We further extend our analysis to transformer models, finding natural correspondences with neural ODEs and their gauge symmetries. The concept of gauge symmetries sheds light on the complex behavior of deep learning models through physics and provides us with a unifying perspective for analyzing various machine learning architectures.