Topological Uncertainty for Anomaly Detection in the Neural-network EoS Inference with Neutron Star Data

We study the performance of the Topological Uncertainty (TU) constructed with a trained feedforward neural network (FNN) for Anomaly Detection. Generally, meaningful information can be stored in the hidden layers of the trained FNN, and the TU implementation is one tractable recipe to extract buried information by means of the Topological Data Analysis. We explicate the concept of the TU and the numerical procedures. Then, for a concrete demonstration of the performance test, we employ the Neutron Star data used for inference of the equation of state (EoS). For the training dataset consisting of the input (Neutron Star data) and the output (EoS parameters), we can compare the inferred EoSs and the exact answers to classify the data with the label $k$. The subdataset with $k=0$ leads to the normal inference for which the inferred EoS approximates the answer well, while the subdataset with $k=1$ ends up with the unsuccessful inference. Once the TU is prepared based on the $k$-labled subdatasets, we introduce the cross-TU to quantify the uncertainty of characterizing the $k$-labeled data with the label $j$. The anomaly or unsuccessful inference is correctly detected if the cross-TU for $j=k=1$ is smaller than that for $j=0$ and $k=1$. In our numerical experiment, for various input data, we calculate the cross-TU and estimate the performance of Anomaly Detection. We find that performance depends on FNN hyperparameters, and the success rate of Anomaly Detection exceeds $90\%$ in the best case. We finally discuss further potential of the TU application to retrieve the information hidden in the trained FNN.

Physics-Driven Learning for Inverse Problems in Quantum Chromodynamics

The integration of deep learning techniques and physics-driven designs is reforming the way we address inverse problems, in which accurate physical properties are extracted from complex data sets. This is particularly relevant for quantum chromodynamics (QCD), the theory of strong interactions, with its inherent limitations in observational data and demanding computational approaches. This perspective highlights advances and potential of physics-driven learning methods, focusing on predictions of physical quantities towards QCD physics, and drawing connections to machine learning(ML). It is shown that the fusion of ML and physics can lead to more efficient and reliable problem-solving strategies. Key ideas of ML, methodology of embedding physics priors, and generative models as inverse modelling of physical probability distributions are introduced. Specific applications cover first-principle lattice calculations, and QCD physics of hadrons, neutron stars, and heavy-ion collisions. These examples provide a structured and concise overview of how incorporating prior knowledge such as symmetry, continuity and equations into deep learning designs can address diverse inverse problems across different physical sciences.

Understanding Diffusion Models by Feynman's Path Integral

Score-based diffusion models have proven effective in image generation and have gained widespread usage; however, the underlying factors contributing to the performance disparity between stochastic and deterministic (i.e., the probability flow ODEs) sampling schemes remain unclear. We introduce a novel formulation of diffusion models using Feynman's path integral, which is a formulation originally developed for quantum physics. We find this formulation providing comprehensive descriptions of score-based generative models, and demonstrate the derivation of backward stochastic differential equations and loss functions.The formulation accommodates an interpolating parameter connecting stochastic and deterministic sampling schemes, and we identify this parameter as a counterpart of Planck's constant in quantum physics. This analogy enables us to apply the Wentzel-Kramers-Brillouin (WKB) expansion, a well-established technique in quantum physics, for evaluating the negative log-likelihood to assess the performance disparity between stochastic and deterministic sampling schemes.

Extensive Studies of the Neutron Star Equation of State from the Deep Learning Inference with the Observational Data Augmentation

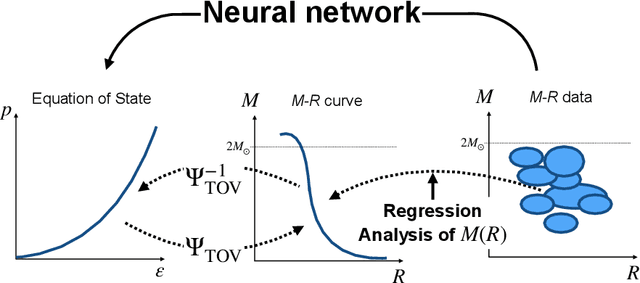
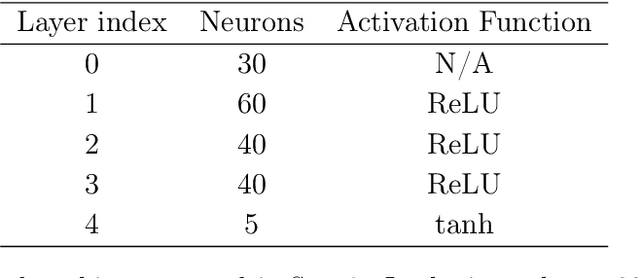
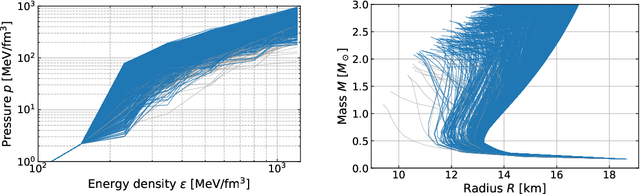
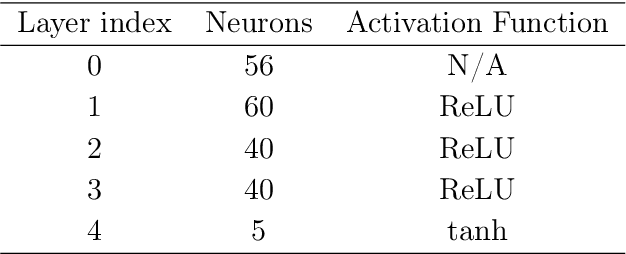
We discuss deep learning inference for the neutron star equation of state (EoS) using the real observational data of the mass and the radius. We make a quantitative comparison between the conventional polynomial regression and the neural network approach for the EoS parametrization. For our deep learning method to incorporate uncertainties in observation, we augment the training data with noise fluctuations corresponding to observational uncertainties. Deduced EoSs can accommodate a weak first-order phase transition, and we make a histogram for likely first-order regions. We also find that our observational data augmentation has a byproduct to tame the overfitting behavior. To check the performance improved by the data augmentation, we set up a toy model as the simplest inference problem to recover a double-peaked function and monitor the validation loss. We conclude that the data augmentation could be a useful technique to evade the overfitting without tuning the neural network architecture such as inserting the dropout.

Featuring the topology with the unsupervised machine learning

Images of line drawings are generally composed of primitive elements. One of the most fundamental elements to characterize images is the topology; line segments belong to a category different from closed circles, and closed circles with different winding degrees are nonequivalent. We investigate images with nontrivial winding using the unsupervised machine learning. We build an autoencoder model with a combination of convolutional and fully connected neural networks. We confirm that compressed data filtered from the trained model retain more than 90% of correct information on the topology, evidencing that image clustering from the unsupervised learning features the topology.