Understanding Diffusion Models by Feynman's Path Integral

Score-based diffusion models have proven effective in image generation and have gained widespread usage; however, the underlying factors contributing to the performance disparity between stochastic and deterministic (i.e., the probability flow ODEs) sampling schemes remain unclear. We introduce a novel formulation of diffusion models using Feynman's path integral, which is a formulation originally developed for quantum physics. We find this formulation providing comprehensive descriptions of score-based generative models, and demonstrate the derivation of backward stochastic differential equations and loss functions.The formulation accommodates an interpolating parameter connecting stochastic and deterministic sampling schemes, and we identify this parameter as a counterpart of Planck's constant in quantum physics. This analogy enables us to apply the Wentzel-Kramers-Brillouin (WKB) expansion, a well-established technique in quantum physics, for evaluating the negative log-likelihood to assess the performance disparity between stochastic and deterministic sampling schemes.

Bézier Flow: a Surface-wise Gradient Descent Method for Multi-objective Optimization

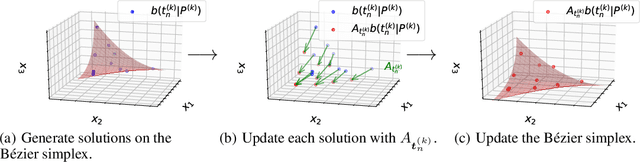
In this paper, we propose a strategy to construct a multi-objective optimization algorithm from a single-objective optimization algorithm by using the B\'ezier simplex model. Also, we extend the stability of optimization algorithms in the sense of Probability Approximately Correct (PAC) learning and define the PAC stability. We prove that it leads to an upper bound on the generalization with high probability. Furthermore, we show that multi-objective optimization algorithms derived from a gradient descent-based single-objective optimization algorithm are PAC stable. We conducted numerical experiments and demonstrated that our method achieved lower generalization errors than the existing multi-objective optimization algorithm.

Approximate Bayesian Computation of Bézier Simplices

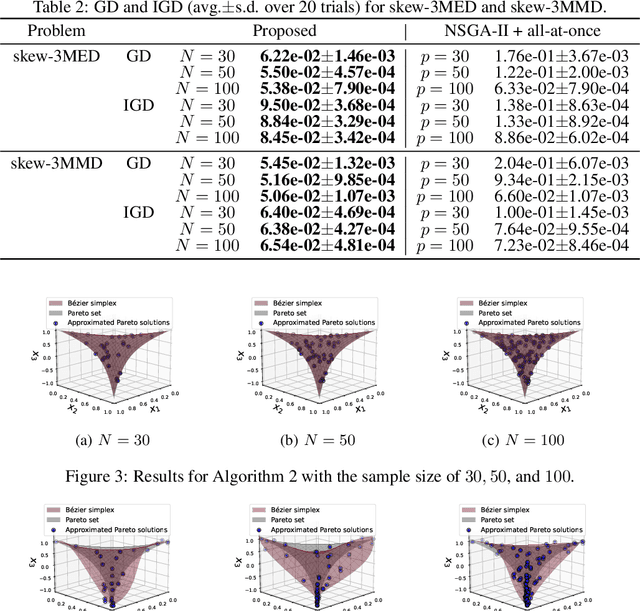
B\'ezier simplex fitting algorithms have been recently proposed to approximate the Pareto set/front of multi-objective continuous optimization problems. These new methods have shown to be successful at approximating various shapes of Pareto sets/fronts when sample points exactly lie on the Pareto set/front. However, if the sample points scatter away from the Pareto set/front, those methods often likely suffer from over-fitting. To overcome this issue, in this paper, we extend the B\'ezier simplex model to a probabilistic one and propose a new learning algorithm of it, which falls into the framework of approximate Bayesian computation (ABC) based on the Wasserstein distance. We also study the convergence property of the Wasserstein ABC algorithm. An extensive experimental evaluation on publicly available problem instances shows that the new algorithm converges on a finite sample. Moreover, it outperforms the deterministic fitting methods on noisy instances.

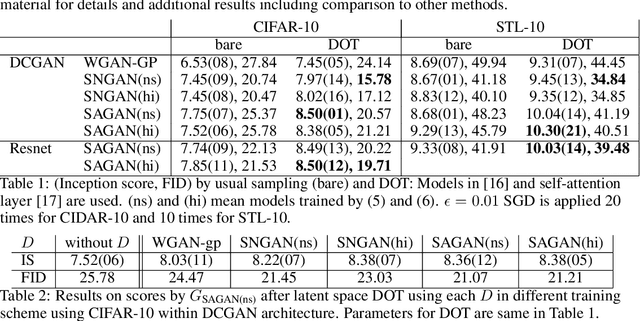
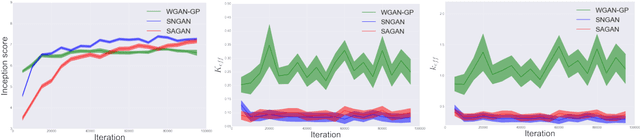
Discriminator optimal transport

Within a broad class of generative adversarial networks, we show that discriminator optimization process increases a lower bound of the dual cost function for the Wasserstein distance between the target distribution $p$ and the generator distribution $p_G$. It implies that the trained discriminator can approximate optimal transport (OT) from $p_G$ to $p$.Based on some experiments and a bit of OT theory, we propose a discriminator optimal transport (DOT) scheme to improve generated images. We show that it improves inception score and FID calculated by un-conditional GAN trained by CIFAR-10, STL-10 and a public pre-trained model of conditional GAN by ImageNet.

Metric on random dynamical systems with vector-valued reproducing kernel Hilbert spaces

The development of a metric on structural data-generating mechanisms is fundamental in machine learning and the related fields. In this paper, we consider a general framework to construct metrics on {\em random} nonlinear dynamical systems, which are defined with the Perron-Frobenius operators in vector-valued reproducing kernel Hilbert spaces (vvRKHSs). Here, vvRKHSs are employed to design mathematically manageable metrics and also to introduce $L^2(\Omega)$-valued kernels, which are necessary to handle the randomness in systems. Our metric is a natural extension of existing metrics for {\em deterministic} systems, and can give a specification of the kernel maximal mean discrepancy of random processes. Moreover, by considering the time-wise independence of random processes, we discuss the connection between our metric and the independence criteria with kernels such as Hilbert-Schmidt independence criteria. We empirically illustrate our metric with synthetic data, and evaluate it in the context of the independence test for random processes.

Asymptotic Risk of Bezier Simplex Fitting

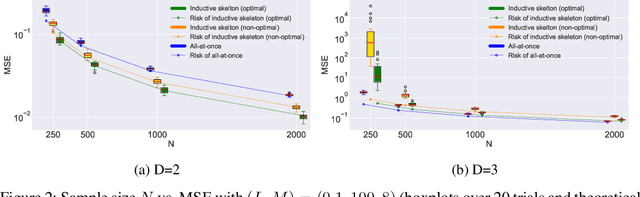
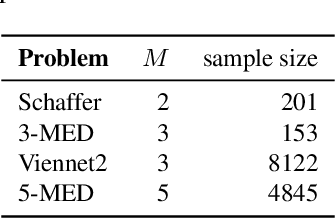
The Bezier simplex fitting is a novel data modeling technique which exploits geometric structures of data to approximate the Pareto front of multi-objective optimization problems. There are two fitting methods based on different sampling strategies. The inductive skeleton fitting employs a stratified subsampling from each skeleton of a simplex, whereas the all-at-once fitting uses a non-stratified sampling which treats a simplex as a whole. In this paper, we analyze the asymptotic risks of those B\'ezier simplex fitting methods and derive the optimal subsample ratio for the inductive skeleton fitting. It is shown that the inductive skeleton fitting with the optimal ratio has a smaller risk when the degree of a Bezier simplex is less than three. Those results are verified numerically under small to moderate sample sizes. In addition, we provide two complementary applications of our theory: a generalized location problem and a multi-objective hyper-parameter tuning of the group lasso. The former can be represented by a Bezier simplex of degree two where the inductive skeleton fitting outperforms. The latter can be represented by a Bezier simplex of degree three where the all-at-once fitting gets an advantage.

Towards reduction of autocorrelation in HMC by machine learning

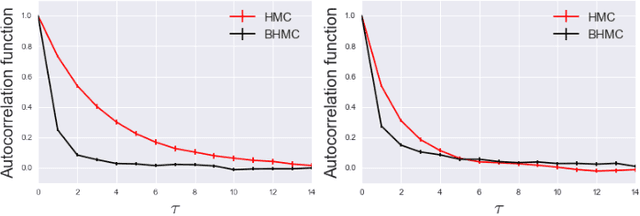
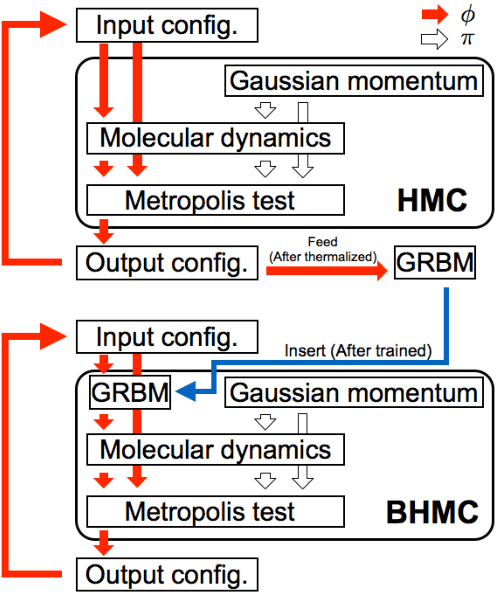
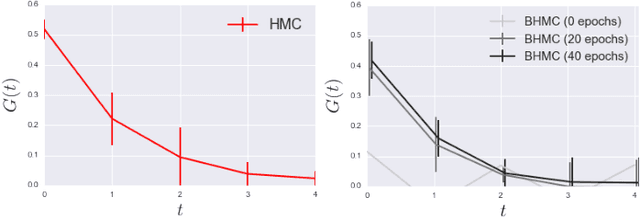
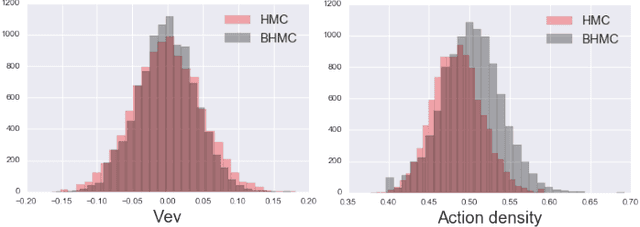
In this paper we propose new algorithm to reduce autocorrelation in Markov chain Monte-Carlo algorithms for euclidean field theories on the lattice. Our proposing algorithm is the Hybrid Monte-Carlo algorithm (HMC) with restricted Boltzmann machine. We examine the validity of the algorithm by employing the phi-fourth theory in three dimension. We observe reduction of the autocorrelation both in symmetric and broken phase as well. Our proposing algorithm provides consistent central values of expectation values of the action density and one-point Green's function with ones from the original HMC in both the symmetric phase and broken phase within the statistical error. On the other hand, two-point Green's functions have slight difference between one calculated by the HMC and one by our proposing algorithm in the symmetric phase. Furthermore, near the criticality, the distribution of the one-point Green's function differs from the one from HMC. We discuss the origin of discrepancies and its improvement.