Equivariant Transformer is all you need

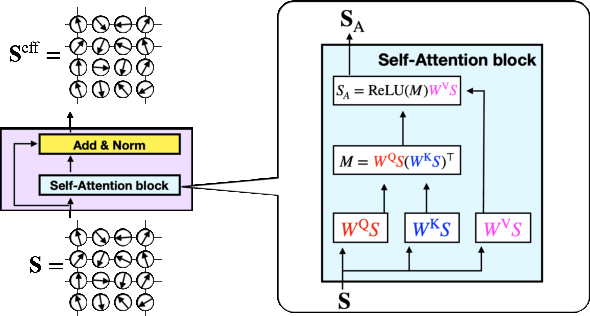
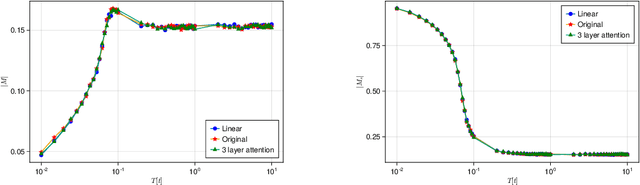
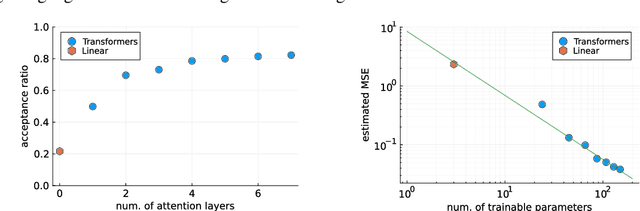
Machine learning, deep learning, has been accelerating computational physics, which has been used to simulate systems on a lattice. Equivariance is essential to simulate a physical system because it imposes a strong induction bias for the probability distribution described by a machine learning model. This reduces the risk of erroneous extrapolation that deviates from data symmetries and physical laws. However, imposing symmetry on the model sometimes occur a poor acceptance rate in self-learning Monte-Carlo (SLMC). On the other hand, Attention used in Transformers like GPT realizes a large model capacity. We introduce symmetry equivariant attention to SLMC. To evaluate our architecture, we apply it to our proposed new architecture on a spin-fermion model on a two-dimensional lattice. We find that it overcomes poor acceptance rates for linear models and observe the scaling law of the acceptance rate as in the large language models with Transformers.

HMC with Normalizing Flows

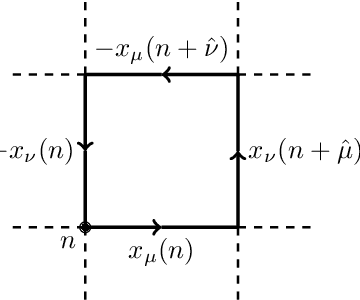
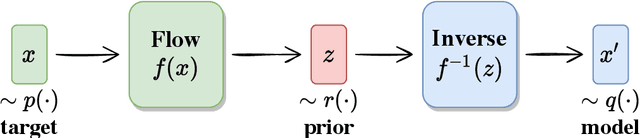
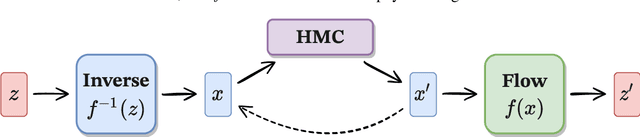
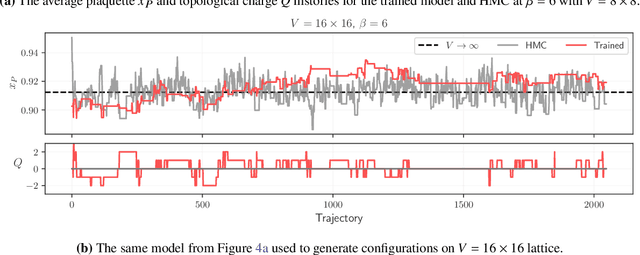
We propose using Normalizing Flows as a trainable kernel within the molecular dynamics update of Hamiltonian Monte Carlo (HMC). By learning (invertible) transformations that simplify our dynamics, we can outperform traditional methods at generating independent configurations. We show that, using a carefully constructed network architecture, our approach can be easily scaled to large lattice volumes with minimal retraining effort. The source code for our implementation is publicly available online at https://github.com/nftqcd/fthmc.

Towards reduction of autocorrelation in HMC by machine learning

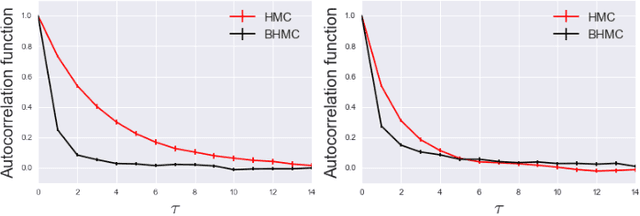
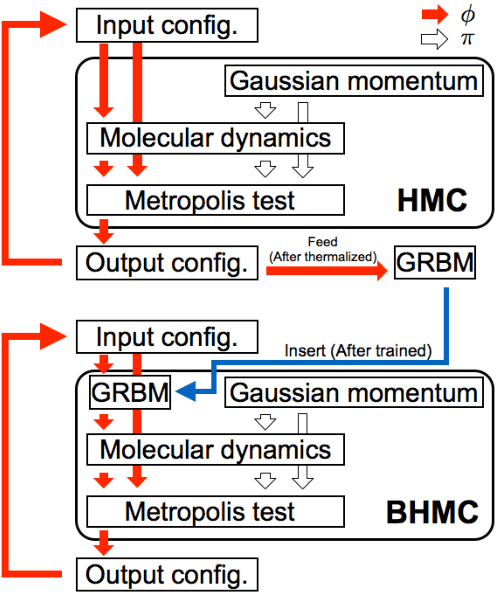
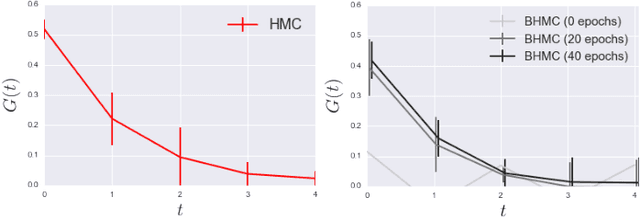
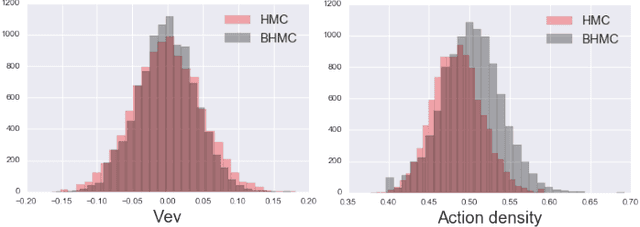
In this paper we propose new algorithm to reduce autocorrelation in Markov chain Monte-Carlo algorithms for euclidean field theories on the lattice. Our proposing algorithm is the Hybrid Monte-Carlo algorithm (HMC) with restricted Boltzmann machine. We examine the validity of the algorithm by employing the phi-fourth theory in three dimension. We observe reduction of the autocorrelation both in symmetric and broken phase as well. Our proposing algorithm provides consistent central values of expectation values of the action density and one-point Green's function with ones from the original HMC in both the symmetric phase and broken phase within the statistical error. On the other hand, two-point Green's functions have slight difference between one calculated by the HMC and one by our proposing algorithm in the symmetric phase. Furthermore, near the criticality, the distribution of the one-point Green's function differs from the one from HMC. We discuss the origin of discrepancies and its improvement.