Towards reduction of autocorrelation in HMC by machine learning
Paper and Code
Dec 11, 2017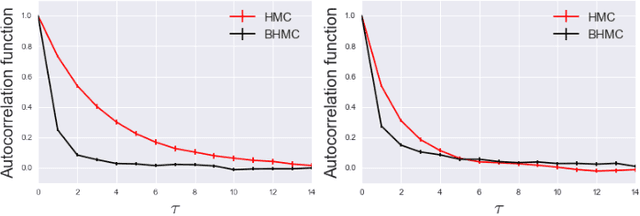
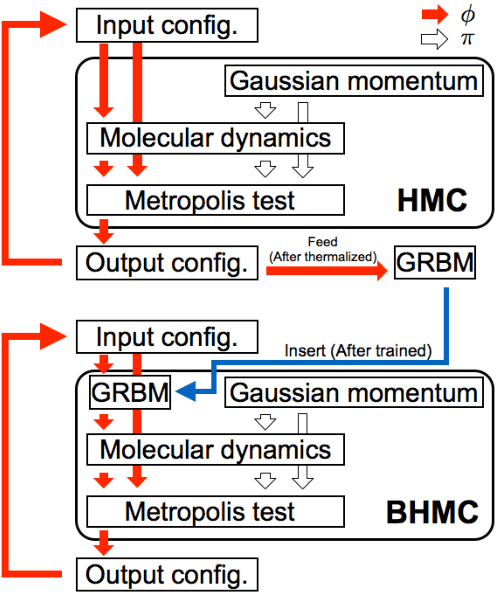
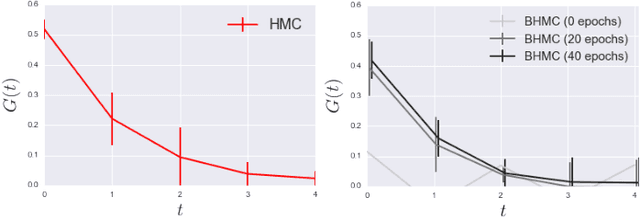
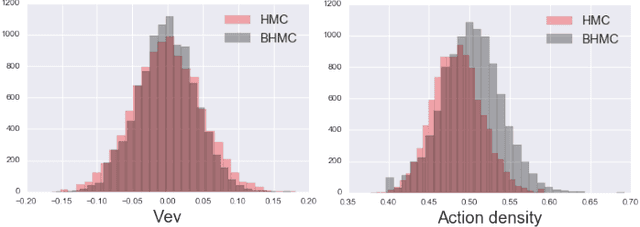
In this paper we propose new algorithm to reduce autocorrelation in Markov chain Monte-Carlo algorithms for euclidean field theories on the lattice. Our proposing algorithm is the Hybrid Monte-Carlo algorithm (HMC) with restricted Boltzmann machine. We examine the validity of the algorithm by employing the phi-fourth theory in three dimension. We observe reduction of the autocorrelation both in symmetric and broken phase as well. Our proposing algorithm provides consistent central values of expectation values of the action density and one-point Green's function with ones from the original HMC in both the symmetric phase and broken phase within the statistical error. On the other hand, two-point Green's functions have slight difference between one calculated by the HMC and one by our proposing algorithm in the symmetric phase. Furthermore, near the criticality, the distribution of the one-point Green's function differs from the one from HMC. We discuss the origin of discrepancies and its improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge