Decomposition of Equivariant Maps via Invariant Maps: Application to Universal Approximation under Symmetry

In this paper, we develop a theory about the relationship between invariant and equivariant maps with regard to a group $G$. We then leverage this theory in the context of deep neural networks with group symmetries in order to obtain novel insight into their mechanisms. More precisely, we establish a one-to-one relationship between equivariant maps and certain invariant maps. This allows us to reduce arguments for equivariant maps to those for invariant maps and vice versa. As an application, we propose a construction of universal equivariant architectures built from universal invariant networks. We, in turn, explain how the universal architectures arising from our construction differ from standard equivariant architectures known to be universal. Furthermore, we explore the complexity, in terms of the number of free parameters, of our models, and discuss the relation between invariant and equivariant networks' complexity. Finally, we also give an approximation rate for G-equivariant deep neural networks with ReLU activation functions for finite group G.

Convergence of Message Passing Graph Neural Networks with Generic Aggregation On Large Random Graphs

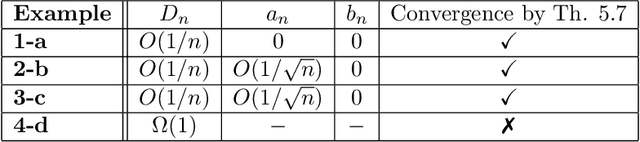
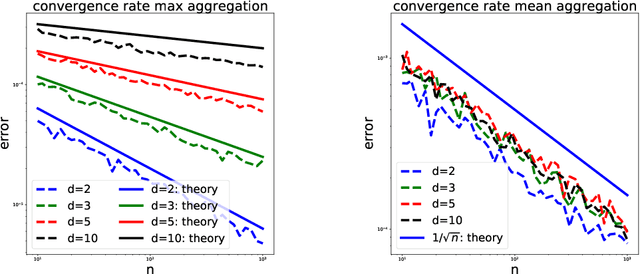
We study the convergence of message passing graph neural networks on random graph models to their continuous counterpart as the number of nodes tends to infinity. Until now, this convergence was only known for architectures with aggregation functions in the form of degree-normalized means. We extend such results to a very large class of aggregation functions, that encompasses all classically used message passing graph neural networks, such as attention-based mesage passing or max convolutional message passing on top of (degree-normalized) convolutional message passing. Under mild assumptions, we give non asymptotic bounds with high probability to quantify this convergence. Our main result is based on the McDiarmid inequality. Interestingly, we treat the case where the aggregation is a coordinate-wise maximum separately, at it necessitates a very different proof technique and yields a qualitatively different convergence rate.

On the Number of Linear Functions Composing Deep Neural Network: Towards a Refined Definition of Neural Networks Complexity

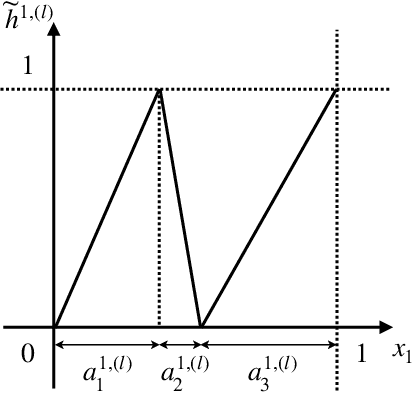
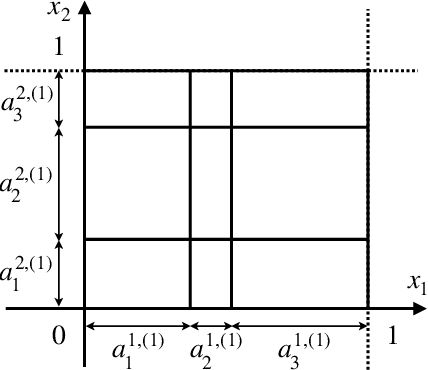
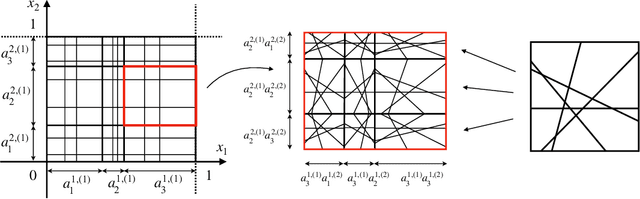
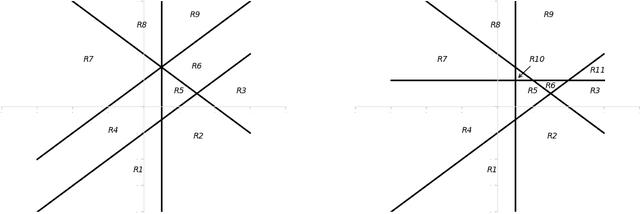
The classical approach to measure the expressive power of deep neural networks with piecewise linear activations is based on counting their maximum number of linear regions. However, when considering the two different models which are the fully connected and the permutation invariant ones, this measure is unable to distinguish them clearly in term of expressivity. To tackle this, we propose a refined definition of deep neural networks complexity. Instead of counting the number of linear regions directly, we first introduce an equivalence relation between the linear functions composing a DNN and then count those functions relatively to that equivalence relation. We continue with a study of our new complexity measure and verify that it has the good expected properties. It is able to distinguish clearly between the two models mentioned above, it is consistent with the classical measure, and it increases exponentially with depth. That last point confirms the high expressive power of deep networks.

Universal approximations of permutation invariant/equivariant functions by deep neural networks

In this paper,we develop a theory of the relationship between permutation ($S_n$-) invariant/equivariant functions and deep neural networks. As a result, we prove an permutation invariant/equivariant version of the universal approximation theorem, i.e $S_n$-invariant/equivariant deep neural networks. The equivariant models are consist of stacking standard single-layer neural networks $Z_i:X \to Y$ for which every $Z_i$ is $S_n$-equivariant with respect to the actions of $S_n$ . The invariant models are consist of stacking equivariant models and standard single-layer neural networks $Z_i:X \to Y$ for which every $Z_i$ is $S_n$-invariant with respect to the actions of $S_n$ . These are universal approximators to $S_n$-invariant/equivariant functions. The above notation is mathematically natural generalization of the models in \cite{deepsets}. We also calculate the number of free parameters appeared in these models. As a result, the number of free parameters appeared in these models is much smaller than the one of the usual models. Hence, we conclude that although the free parameters of the invariant/equivarint models are exponentially fewer than the one of the usual models, the invariant/equivariant models can approximate the invariant/equivariant functions to arbitrary accuracy. This gives us an understanding of why the invariant/equivariant models designed in [Zaheer et al. 2018] work well.