All unconstrained strongly convex problems are weakly simplicial
Paper and Code
Jun 24, 2021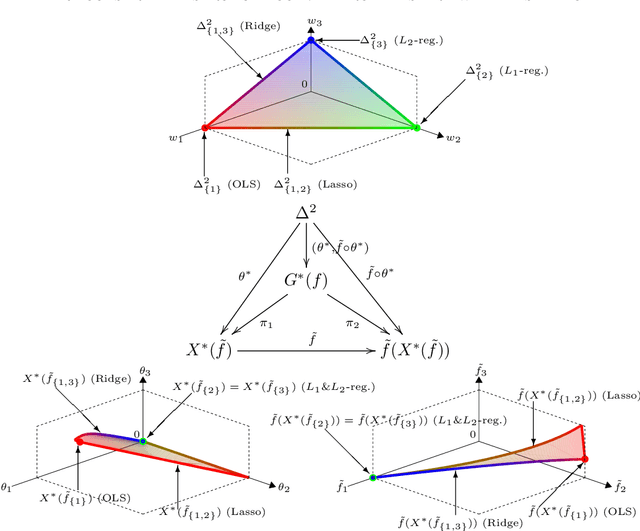
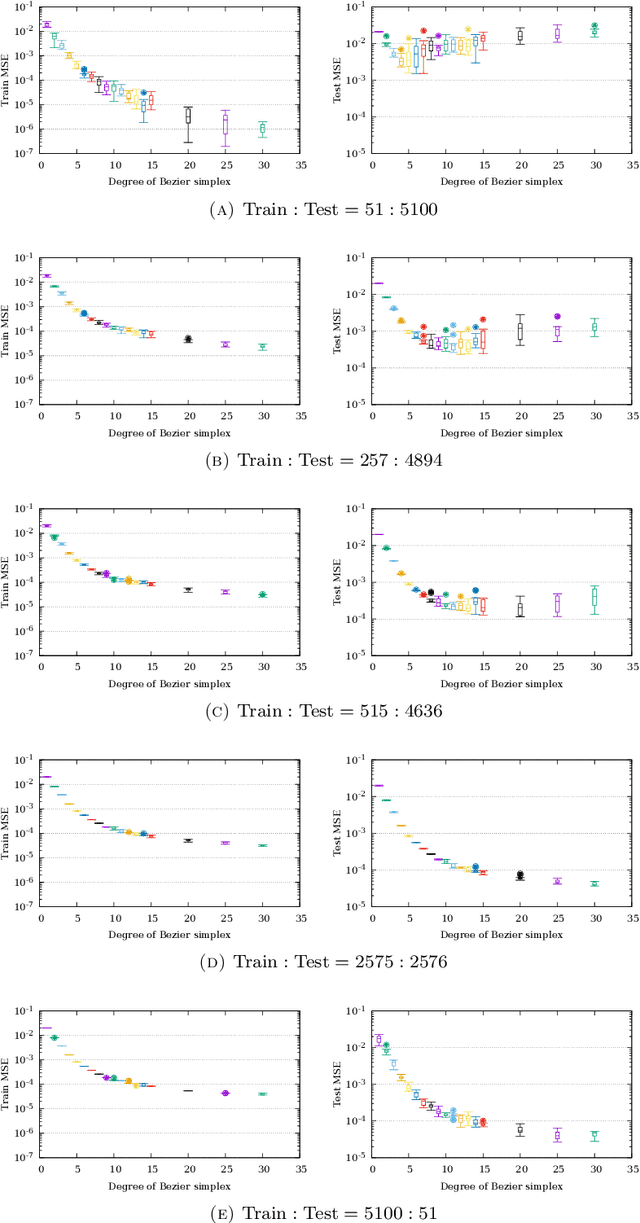
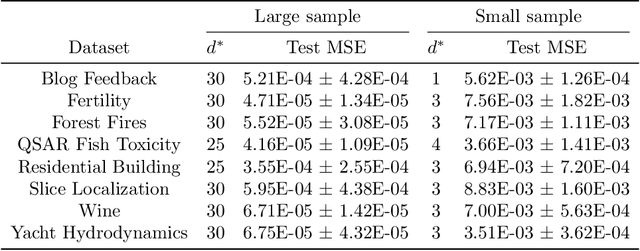
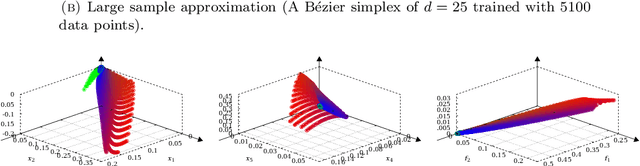
A multi-objective optimization problem is $C^r$ weakly simplicial if there exists a $C^r$ surjection from a simplex onto the Pareto set/front such that the image of each subsimplex is the Pareto set/front of a subproblem, where $0\leq r\leq \infty$. This property is helpful to compute a parametric-surface approximation of the entire Pareto set and Pareto front. It is known that all unconstrained strongly convex $C^r$ problems are $C^{r-1}$ weakly simplicial for $1\leq r \leq \infty$. In this paper, we show that all unconstrained strongly convex problems are $C^0$ weakly simplicial. The usefulness of this theorem is demonstrated in a sparse modeling application: we reformulate the elastic net as a non-differentiable multi-objective strongly convex problem and approximate its Pareto set (the set of all trained models with different hyper-parameters) and Pareto front (the set of performance metrics of the trained models) by using a B\'ezier simplex fitting method, which accelerates hyper-parameter search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge