Neural Operators Meet Energy-based Theory: Operator Learning for Hamiltonian and Dissipative PDEs

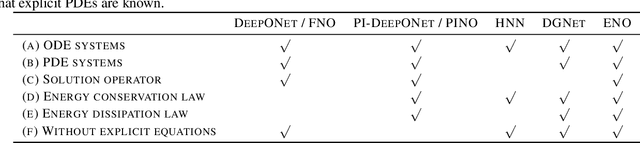
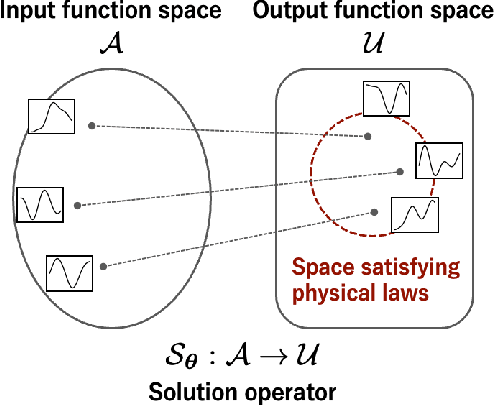
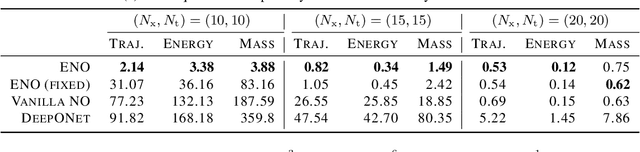
The operator learning has received significant attention in recent years, with the aim of learning a mapping between function spaces. Prior works have proposed deep neural networks (DNNs) for learning such a mapping, enabling the learning of solution operators of partial differential equations (PDEs). However, these works still struggle to learn dynamics that obeys the laws of physics. This paper proposes Energy-consistent Neural Operators (ENOs), a general framework for learning solution operators of PDEs that follows the energy conservation or dissipation law from observed solution trajectories. We introduce a novel penalty function inspired by the energy-based theory of physics for training, in which the energy functional is modeled by another DNN, allowing one to bias the outputs of the DNN-based solution operators to ensure energetic consistency without explicit PDEs. Experiments on multiple physical systems show that ENO outperforms existing DNN models in predicting solutions from data, especially in super-resolution settings.

Meta-learning of Physics-informed Neural Networks for Efficiently Solving Newly Given PDEs

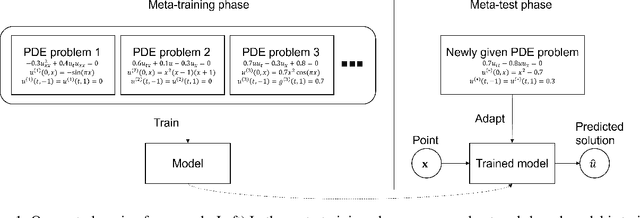
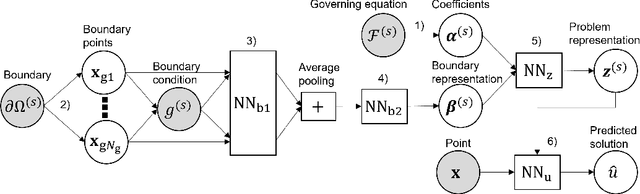
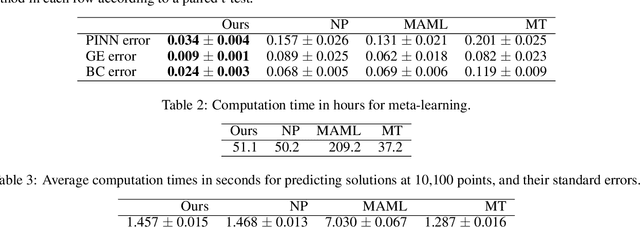
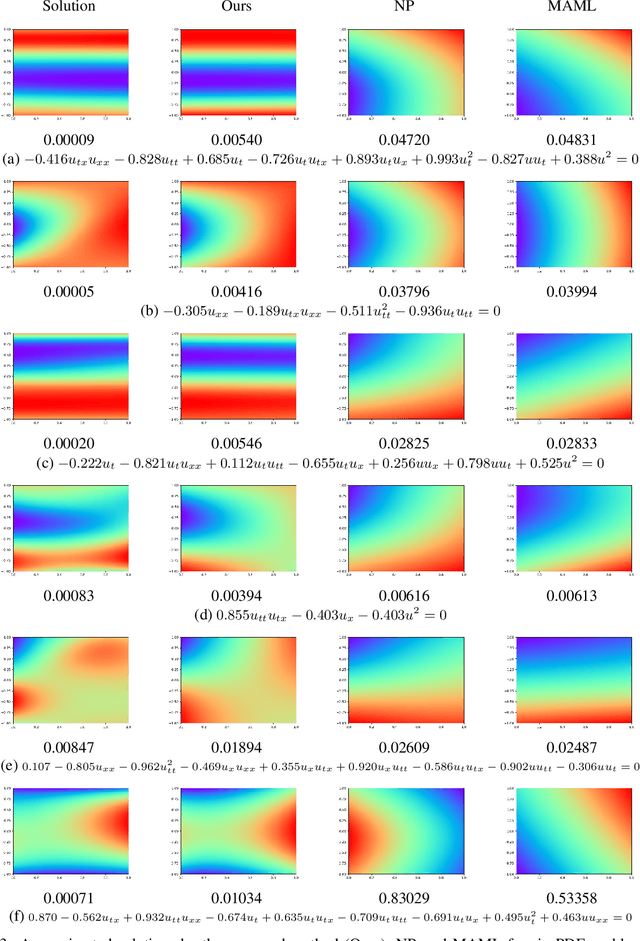
We propose a neural network-based meta-learning method to efficiently solve partial differential equation (PDE) problems. The proposed method is designed to meta-learn how to solve a wide variety of PDE problems, and uses the knowledge for solving newly given PDE problems. We encode a PDE problem into a problem representation using neural networks, where governing equations are represented by coefficients of a polynomial function of partial derivatives, and boundary conditions are represented by a set of point-condition pairs. We use the problem representation as an input of a neural network for predicting solutions, which enables us to efficiently predict problem-specific solutions by the forwarding process of the neural network without updating model parameters. To train our model, we minimize the expected error when adapted to a PDE problem based on the physics-informed neural network framework, by which we can evaluate the error even when solutions are unknown. We demonstrate that our proposed method outperforms existing methods in predicting solutions of PDE problems.

Excess risk analysis for epistemic uncertainty with application to variational inference

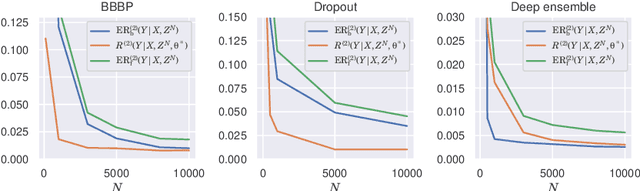
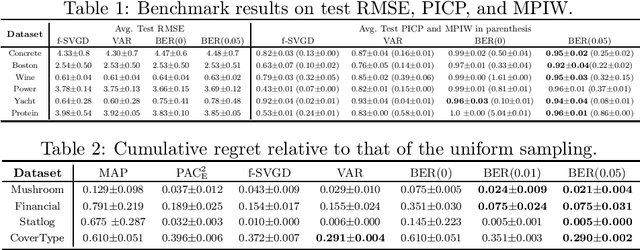
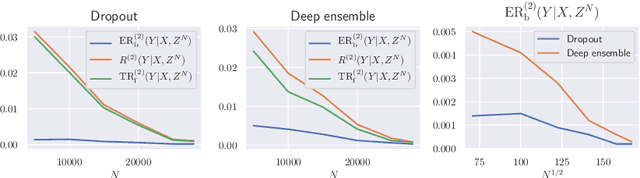
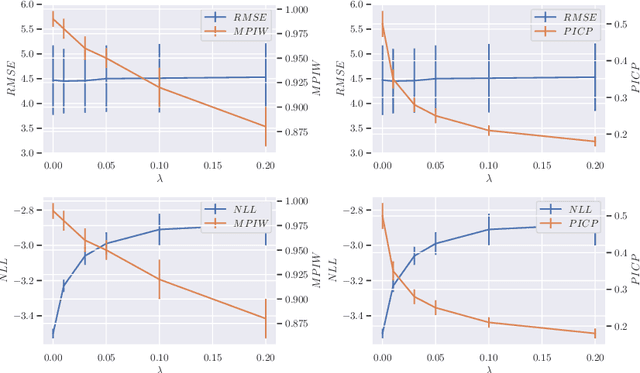
We analyze the epistemic uncertainty (EU) of supervised learning in Bayesian inference by focusing on the excess risk. Existing analysis is limited to the Bayesian setting, which assumes a correct model and exact Bayesian posterior distribution. Thus we cannot apply the existing theory to modern Bayesian algorithms, such as variational inference. To address this, we present a novel EU analysis in the frequentist setting, where data is generated from an unknown distribution. We show a relation between the generalization ability and the widely used EU measurements, such as the variance and entropy of the predictive distribution. Then we show their convergence behaviors theoretically. Finally, we propose new variational inference that directly controls the prediction and EU evaluation performances based on the PAC-Bayesian theory. Numerical experiments show that our algorithm significantly improves the EU evaluation over the existing methods.

Loss function based second-order Jensen inequality and its application to particle variational inference

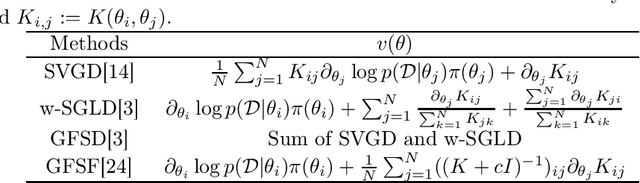
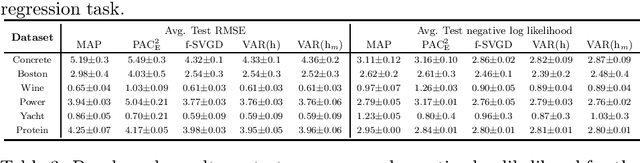
Bayesian model averaging, obtained as the expectation of a likelihood function by a posterior distribution, has been widely used for prediction, evaluation of uncertainty, and model selection. Various approaches have been developed to efficiently capture the information in the posterior distribution; one such approach is the optimization of a set of models simultaneously with interaction to ensure the diversity of the individual models in the same way as ensemble learning. A representative approach is particle variational inference (PVI), which uses an ensemble of models as an empirical approximation for the posterior distribution. PVI iteratively updates each model with a repulsion force to ensure the diversity of the optimized models. However, despite its promising performance, a theoretical understanding of this repulsion and its association with the generalization ability remains unclear. In this paper, we tackle this problem in light of PAC-Bayesian analysis. First, we provide a new second-order Jensen inequality, which has the repulsion term based on the loss function. Thanks to the repulsion term, it is tighter than the standard Jensen inequality. Then, we derive a novel generalization error bound and show that it can be reduced by enhancing the diversity of models. Finally, we derive a new PVI that optimizes the generalization error bound directly. Numerical experiments demonstrate that the performance of the proposed PVI compares favorably with existing methods in the experiment.

Translation Between Waves, wave2wave

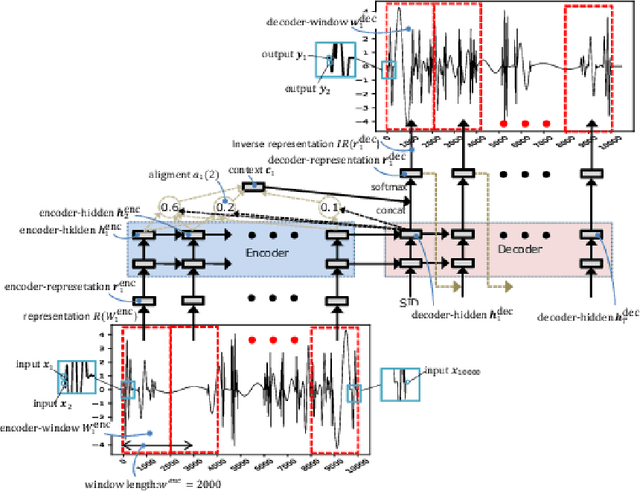
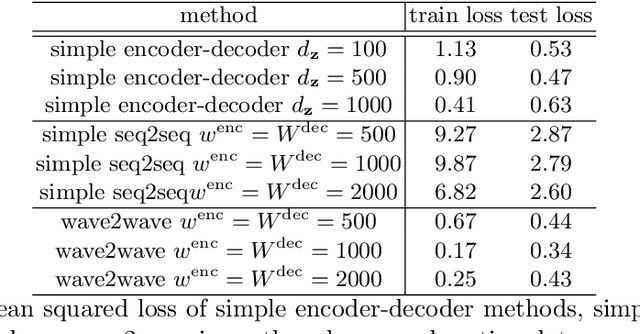
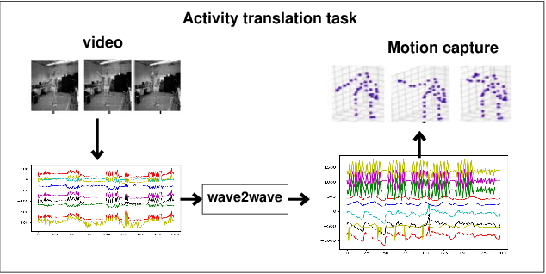
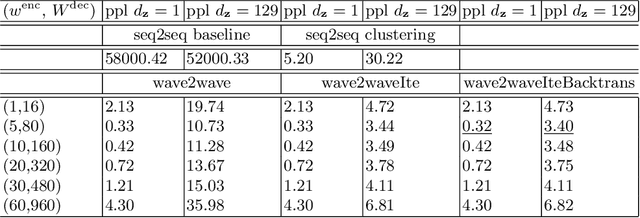
The understanding of sensor data has been greatly improved by advanced deep learning methods with big data. However, available sensor data in the real world are still limited, which is called the opportunistic sensor problem. This paper proposes a new variant of neural machine translation seq2seq to deal with continuous signal waves by introducing the window-based (inverse-) representation to adaptively represent partial shapes of waves and the iterative back-translation model for high-dimensional data. Experimental results are shown for two real-life data: earthquake and activity translation. The performance improvements of one-dimensional data was about 46% in test loss and that of high-dimensional data was about 1625% in perplexity with regard to the original seq2seq.

Anomaly Detection with Inexact Labels

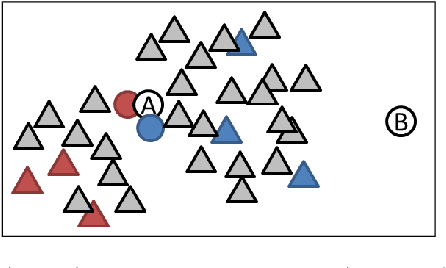
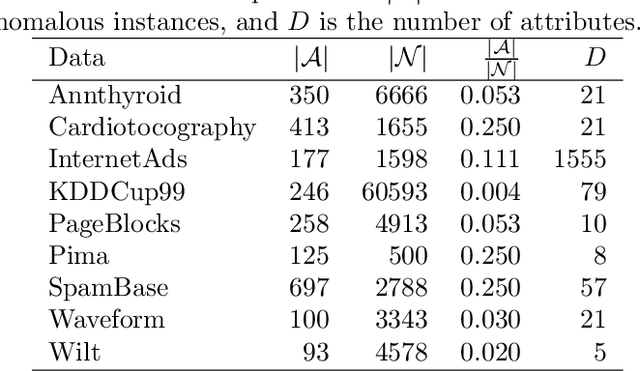
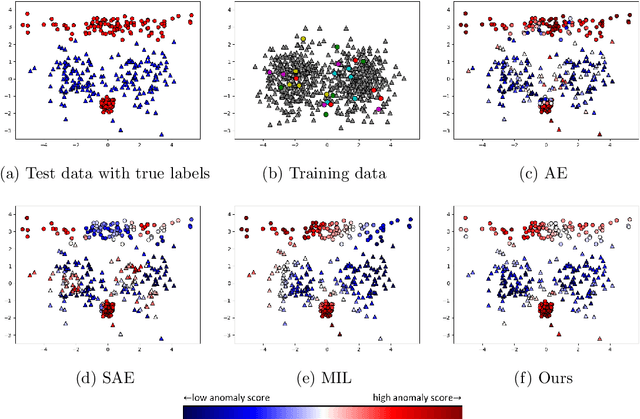
We propose a supervised anomaly detection method for data with inexact anomaly labels, where each label, which is assigned to a set of instances, indicates that at least one instance in the set is anomalous. Although many anomaly detection methods have been proposed, they cannot handle inexact anomaly labels. To measure the performance with inexact anomaly labels, we define the inexact AUC, which is our extension of the area under the ROC curve (AUC) for inexact labels. The proposed method trains an anomaly score function so that the smooth approximation of the inexact AUC increases while anomaly scores for non-anomalous instances become low. We model the anomaly score function by a neural network-based unsupervised anomaly detection method, e.g., autoencoders. The proposed method performs well even when only a small number of inexact labels are available by incorporating an unsupervised anomaly detection mechanism with inexact AUC maximization. Using various datasets, we experimentally demonstrate that our proposed method improves the anomaly detection performance with inexact anomaly labels, and outperforms existing unsupervised and supervised anomaly detection and multiple instance learning methods.

Deep Mixture Point Processes: Spatio-temporal Event Prediction with Rich Contextual Information

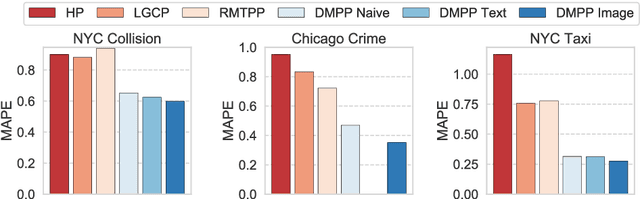
Predicting when and where events will occur in cities, like taxi pick-ups, crimes, and vehicle collisions, is a challenging and important problem with many applications in fields such as urban planning, transportation optimization and location-based marketing. Though many point processes have been proposed to model events in a continuous spatio-temporal space, none of them allow for the consideration of the rich contextual factors that affect event occurrence, such as weather, social activities, geographical characteristics, and traffic. In this paper, we propose \textsf{DMPP} (Deep Mixture Point Processes), a point process model for predicting spatio-temporal events with the use of rich contextual information; a key advance is its incorporation of the heterogeneous and high-dimensional context available in image and text data. Specifically, we design the intensity of our point process model as a mixture of kernels, where the mixture weights are modeled by a deep neural network. This formulation allows us to automatically learn the complex nonlinear effects of the contextual factors on event occurrence. At the same time, this formulation makes analytical integration over the intensity, which is required for point process estimation, tractable. We use real-world data sets from different domains to demonstrate that DMPP has better predictive performance than existing methods.

Fully Neural Network based Model for General Temporal Point Processes

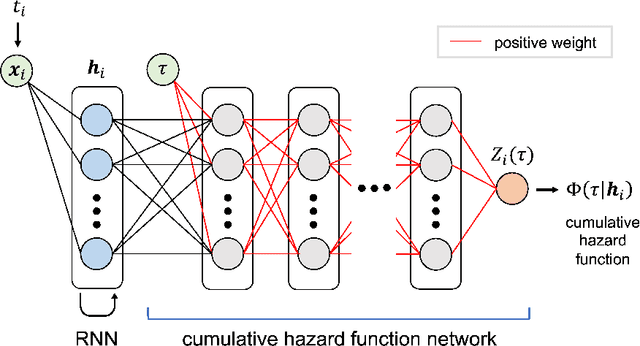
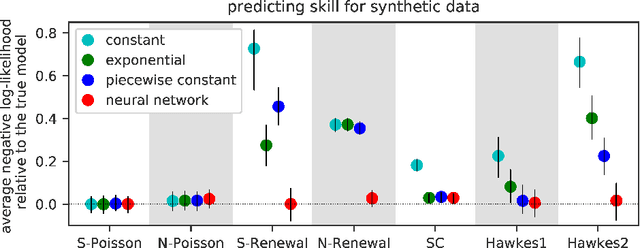
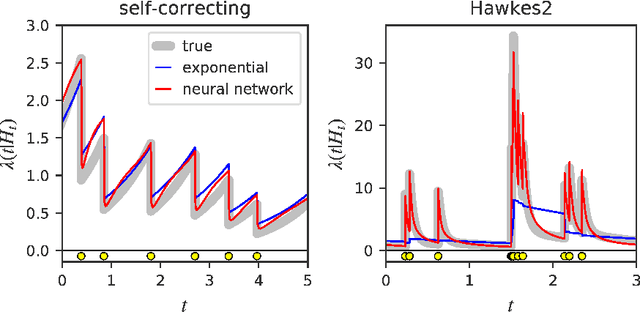
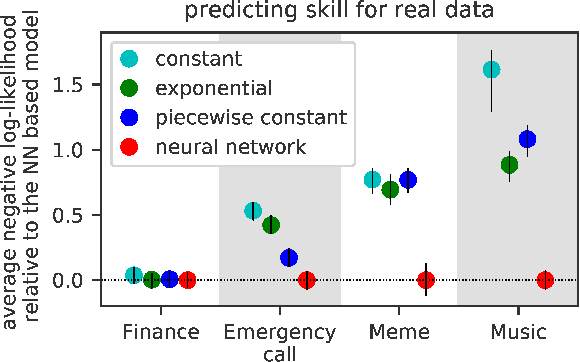
A temporal point process is a mathematical model for a time series of discrete events, which covers various applications. Recently, recurrent neural network (RNN) based models have been developed for point processes and have been found effective. RNN based models usually assume a specific functional form for the time course of the intensity function of a point process (e.g., exponentially decreasing or increasing with the time since the most recent event). However, such an assumption can restrict the expressive power of the model. We herein propose a novel RNN based model in which the time course of the intensity function is represented in a general manner. In our approach, we first model the integral of the intensity function using a feedforward neural network and then obtain the intensity function as its derivative. This approach enables us to both obtain a flexible model of the intensity function and exactly evaluate the log-likelihood function, which contains the integral of the intensity function, without any numerical approximations. Our model achieves competitive or superior performances compared to the previous state-of-the-art methods for both synthetic and real datasets.

Unsupervised Object Matching for Relational Data

We propose an unsupervised object matching method for relational data, which finds matchings between objects in different relational datasets without correspondence information. For example, the proposed method matches documents in different languages in multi-lingual document-word networks without dictionaries nor alignment information. The proposed method assumes that each object has latent vectors, and the probability of neighbor objects is modeled by the inner-product of the latent vectors, where the neighbors are generated by short random walks over the relations. The latent vectors are estimated by maximizing the likelihood of the neighbors for each dataset. The estimated latent vectors contain hidden structural information of each object in the given relational dataset. Then, the proposed method linearly projects the latent vectors for all the datasets onto a common latent space shared across all datasets by matching the distributions while preserving the structural information. The projection matrix is estimated by minimizing the distance between the latent vector distributions with an orthogonality regularizer. To represent the distributions effectively, we use the kernel embedding of distributions that hold high-order moment information about a distribution as an element in a reproducing kernel Hilbert space, which enables us to calculate the distance between the distributions without density estimation. The structural information encoded in the latent vectors are preserved by using the orthogonality regularizer. We demonstrate the effectiveness of the proposed method with experiments using real-world multi-lingual document-word relational datasets and multiple user-item relational datasets.

Finding Appropriate Traffic Regulations via Graph Convolutional Networks

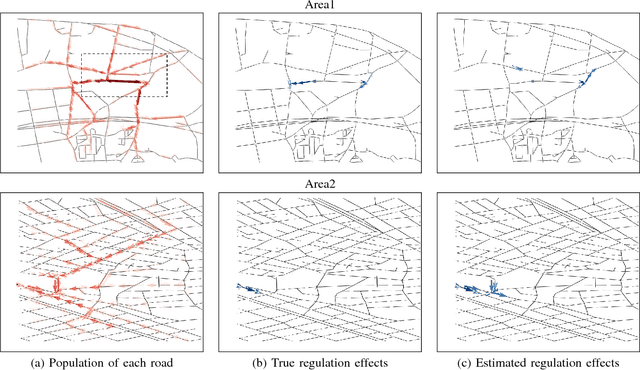
Appropriate traffic regulations, e.g. planned road closure, are important in congested events. Crowd simulators have been used to find appropriate regulations by simulating multiple scenarios with different regulations. However, this approach requires multiple simulation runs, which are time-consuming. In this paper, we propose a method to learn a function that outputs regulation effects given the current traffic situation as inputs. If the function is learned using the training data of many simulation runs in advance, we can obtain an appropriate regulation efficiently by bypassing simulations for the current situation. We use the graph convolutional networks for modeling the function, which enable us to find regulations even for unseen areas. With the proposed method, we construct a graph for each area, where a node represents a road, and an edge represents the road connection. By running crowd simulations with various regulations on various areas, we generate traffic situations and regulation effects. The graph convolutional networks are trained to output the regulation effects given the graph with the traffic situation information as inputs. With experiments using real-world road networks and a crowd simulator, we demonstrate that the proposed method can find a road to close that reduces the average time needed to reach the destination.