Efficient Transfer Bayesian Optimization with Auxiliary Information

We propose an efficient transfer Bayesian optimization method, which finds the maximum of an expensive-to-evaluate black-box function by using data on related optimization tasks. Our method uses auxiliary information that represents the task characteristics to effectively transfer knowledge for estimating a distribution over target functions. In particular, we use a Gaussian process, in which the mean and covariance functions are modeled with neural networks that simultaneously take both the auxiliary information and feature vectors as input. With a neural network mean function, we can estimate the target function even without evaluations. By using the neural network covariance function, we can extract nonlinear correlation among feature vectors that are shared across related tasks. Our Gaussian process-based formulation not only enables an analytic calculation of the posterior distribution but also swiftly adapts the target function to observations. Our method is also advantageous because the computational costs scale linearly with the number of source tasks. Through experiments using a synthetic dataset and datasets for finding the optimal pedestrian traffic regulations and optimal machine learning algorithms, we demonstrate that our method identifies the optimal points with fewer target function evaluations than existing methods.

On Transformations in Stochastic Gradient MCMC

Stochastic gradient Langevin dynamics (SGLD) is a widely used sampler for the posterior inference with a large scale dataset. Although SGLD is designed for unbounded random variables, many practical models incorporate variables with boundaries such as non-negative ones or those in a finite interval. Existing modifications of SGLD for handling bounded random variables resort to heuristics without a formal guarantee of sampling from the true stationary distribution. In this paper, we reformulate the SGLD algorithm incorporating a deterministic transformation with rigorous theories. Our method transforms unbounded samples obtained by SGLD into the domain of interest. We demonstrate transformed SGLD in both artificial problem settings and real-world applications of Bayesian non-negative matrix factorization and binary neural networks.

Finding Appropriate Traffic Regulations via Graph Convolutional Networks

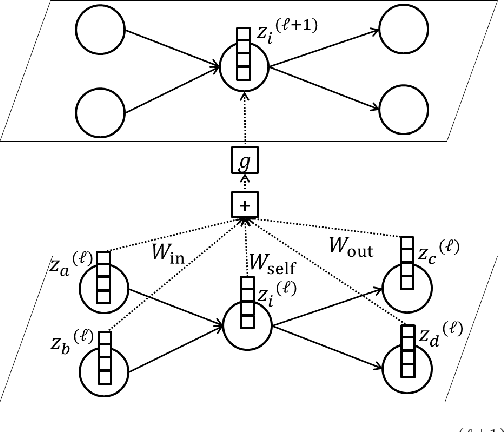
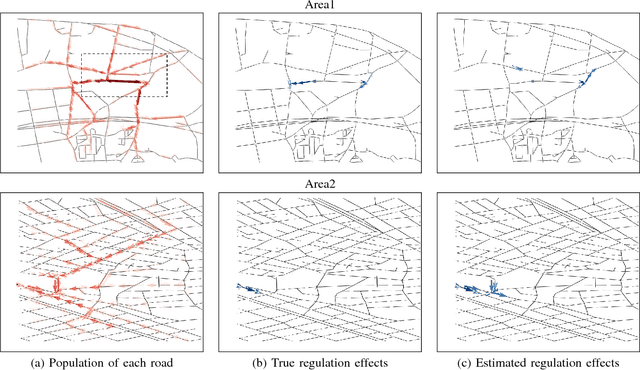
Appropriate traffic regulations, e.g. planned road closure, are important in congested events. Crowd simulators have been used to find appropriate regulations by simulating multiple scenarios with different regulations. However, this approach requires multiple simulation runs, which are time-consuming. In this paper, we propose a method to learn a function that outputs regulation effects given the current traffic situation as inputs. If the function is learned using the training data of many simulation runs in advance, we can obtain an appropriate regulation efficiently by bypassing simulations for the current situation. We use the graph convolutional networks for modeling the function, which enable us to find regulations even for unseen areas. With the proposed method, we construct a graph for each area, where a node represents a road, and an edge represents the road connection. By running crowd simulations with various regulations on various areas, we generate traffic situations and regulation effects. The graph convolutional networks are trained to output the regulation effects given the graph with the traffic situation information as inputs. With experiments using real-world road networks and a crowd simulator, we demonstrate that the proposed method can find a road to close that reduces the average time needed to reach the destination.

Multi-output Polynomial Networks and Factorization Machines

Factorization machines and polynomial networks are supervised polynomial models based on an efficient low-rank decomposition. We extend these models to the multi-output setting, i.e., for learning vector-valued functions, with application to multi-class or multi-task problems. We cast this as the problem of learning a 3-way tensor whose slices share a common basis and propose a convex formulation of that problem. We then develop an efficient conditional gradient algorithm and prove its global convergence, despite the fact that it involves a non-convex basis selection step. On classification tasks, we show that our algorithm achieves excellent accuracy with much sparser models than existing methods. On recommendation system tasks, we show how to combine our algorithm with a reduction from ordinal regression to multi-output classification and show that the resulting algorithm outperforms simple baselines in terms of ranking accuracy.