Top-Down Bayesian Posterior Sampling for Sum-Product Networks

Sum-product networks (SPNs) are probabilistic models characterized by exact and fast evaluation of fundamental probabilistic operations. Its superior computational tractability has led to applications in many fields, such as machine learning with time constraints or accuracy requirements and real-time systems. The structural constraints of SPNs supporting fast inference, however, lead to increased learning-time complexity and can be an obstacle to building highly expressive SPNs. This study aimed to develop a Bayesian learning approach that can be efficiently implemented on large-scale SPNs. We derived a new full conditional probability of Gibbs sampling by marginalizing multiple random variables to expeditiously obtain the posterior distribution. The complexity analysis revealed that our sampling algorithm works efficiently even for the largest possible SPN. Furthermore, we proposed a hyperparameter tuning method that balances the diversity of the prior distribution and optimization efficiency in large-scale SPNs. Our method has improved learning-time complexity and demonstrated computational speed tens to more than one hundred times faster and superior predictive performance in numerical experiments on more than 20 datasets.

Bayesian interpretation of SGD as Ito process

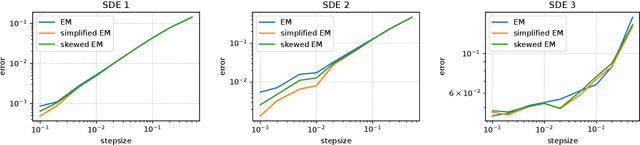
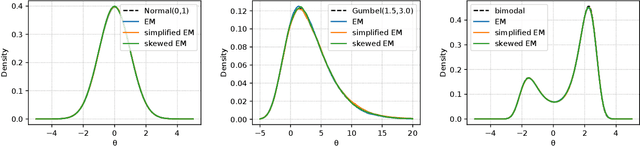
The current interpretation of stochastic gradient descent (SGD) as a stochastic process lacks generality in that its numerical scheme restricts continuous-time dynamics as well as the loss function and the distribution of gradient noise. We introduce a simplified scheme with milder conditions that flexibly interprets SGD as a discrete-time approximation of an Ito process. The scheme also works as a common foundation of SGD and stochastic gradient Langevin dynamics (SGLD), providing insights into their asymptotic properties. We investigate the convergence of SGD with biased gradient in terms of the equilibrium mode and the overestimation problem of the second moment of SGLD.

On Transformations in Stochastic Gradient MCMC

Stochastic gradient Langevin dynamics (SGLD) is a widely used sampler for the posterior inference with a large scale dataset. Although SGLD is designed for unbounded random variables, many practical models incorporate variables with boundaries such as non-negative ones or those in a finite interval. Existing modifications of SGLD for handling bounded random variables resort to heuristics without a formal guarantee of sampling from the true stationary distribution. In this paper, we reformulate the SGLD algorithm incorporating a deterministic transformation with rigorous theories. Our method transforms unbounded samples obtained by SGLD into the domain of interest. We demonstrate transformed SGLD in both artificial problem settings and real-world applications of Bayesian non-negative matrix factorization and binary neural networks.